A vector →F1 is along the positive X-axis. If its vectors product with another vector →F2 is zero then →F2 could be
The correct Answer is:4
To solve the problem step by step, let's analyze the given information and apply the concepts of vectors and their properties.
Step 1: Understand the Given Vectors
We are given that vector →F1 is along the positive X-axis. We can represent this vector as:
→F1=a^i
where a is the magnitude of the vector and ^i is the unit vector in the direction of the X-axis.
Step 2: Vector Product Condition
We know that the vector product (cross product) of →F1 and another vector →F2 is zero:
→F1×→F2=0
The cross product of two vectors is zero if and only if the vectors are parallel or one of the vectors is a zero vector.
Step 3: Express the Cross Product
The magnitude of the cross product can be expressed as:
|→F1×→F2|=|→F1||→F2|sinθ
where θ is the angle between the two vectors. Since the cross product is zero, we can write:
|→F1||→F2|sinθ=0
Step 4: Analyze the Conditions
For the product to be zero, either:
1. |→F1|=0 (which is not the case since →F1 has a magnitude a>0), or
2. |→F2|=0 (which means →F2 is the zero vector), or
3. sinθ=0 (which implies θ=0∘ or θ=180∘).
Step 5: Determine the Implications of θ
If θ=0∘, then →F2 is in the same direction as →F1, meaning:
→F2=b^i
for some scalar b (where b can be positive or negative).
If θ=180∘, then →F2 is in the opposite direction of →F1:
→F2=−b^i
Conclusion
Thus, the vector →F2 could either be in the same direction as →F1 or in the opposite direction. Therefore, →F2 could be represented as:
→F2=b^ior→F2=−b^i
where b is any scalar.
Final Answer
The vector →F2 could be any vector along the X-axis, either in the positive or negative direction.
---
We are given that vector →F1 is along the positive X-axis. We can represent this vector as:
→F1=a^i
where a is the magnitude of the vector and ^i is the unit vector in the direction of the X-axis.
We know that the vector product (cross product) of →F1 and another vector →F2 is zero:
→F1×→F2=0
The cross product of two vectors is zero if and only if the vectors are parallel or one of the vectors is a zero vector.
The magnitude of the cross product can be expressed as:
|→F1×→F2|=|→F1||→F2|sinθ
where θ is the angle between the two vectors. Since the cross product is zero, we can write:
|→F1||→F2|sinθ=0
For the product to be zero, either:
1. |→F1|=0 (which is not the case since →F1 has a magnitude a>0), or
2. |→F2|=0 (which means →F2 is the zero vector), or
3. sinθ=0 (which implies θ=0∘ or θ=180∘).
If θ=0∘, then →F2 is in the same direction as →F1, meaning:
→F2=b^i
for some scalar b (where b can be positive or negative).
→F2=−b^i
Thus, the vector →F2 could either be in the same direction as →F1 or in the opposite direction. Therefore, →F2 could be represented as:
→F2=b^ior→F2=−b^i
where b is any scalar.
The vector →F2 could be any vector along the X-axis, either in the positive or negative direction.
Topper's Solved these Questions
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-II AIPMT/NEET & AIIMS (2006- 2018)
6 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-III CHECK YOUR UNDERSTANDING
15 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - DOT PRODUCT
20 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B
19 Videos
Similar Questions
A vector →F1 is along the positive X-axis. its vectors product with another vector →F2 is ? where →F2 is along Y-axis
View SolutionA vector →A is along the positive z-axis and its vector product with another vector →B is zero, then vector →B could be :
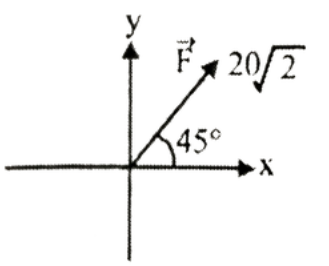
View SolutionWrite the vector →F in terms of its component :-
View SolutionA vector ¯¯¯P is along positive x axis, if ¯¯¯Q is another vector such that (¯¯¯P⋅¯¯¯Q) is zero, then Q should be
View SolutionProve that the scalar product of two or thogonal vectors is zero .
View SolutionA vector →B which has a magnitude 8.0 is added to a vector →A which lies along the x-axis. The sum of these two vector is a third vector which lies along the y-axis and has a magnitude that is twice the magnitude of →A. Find the magnitude of →A
View SolutionA vector ¯¯¯Qwhich has a magnitude of 8 is added to the vector ¯¯¯P which lies along the X-axis. The resultant of these two vectors is a third vector ¯¯¯R which lies along the Y-axis and has a magnitude twice that of ¯¯¯P. The magnitude of ¯¯¯P is
View SolutionConsider a vector →F=4ˆi−3ˆj. Another vector that is perpendicular to →F is
View SolutionThe vector product of two vectors is a zero vector ? What does it imply ?
View SolutionTwo forces →F1=(3N)ˆi−(4N)ˆj and →F2=−(1N)ˆi−(2N)ˆj act on a point object. In the given figure which of the six vectors represents →F1 and →F2 and what is the magnitude of the net forces

View Solution