Write the vector →F in terms of its component :-
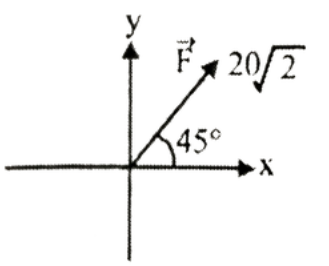
→F=10ˆi+10ˆj
→F=20ˆi+20ˆj
→F=30ˆi+30ˆj
→F=40ˆi+40ˆj
The correct Answer is:B
Step by step video & image solution for Write the vector vecF in terms of its component :- by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Units, Dimensions & Measurements)
30 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (KINEMATICS)
59 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Co-ordinate & Algebra)
37 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
Similar Questions
x- component of a vector →A is twice of its y-component and √2 times of its z-component. Find out the angle made by the vector from y-axis.
View SolutionFor the given vector →A=3ˆi−4ˆj+10ˆk, the ratio of magnitude of its component on the x−y plane and the component on z−axis is
View SolutionFor the given vector →A=3ˆi+4ˆj+10ˆk, the ratio of magnitude of its component on the x−y plane and the component on z−axis is
View SolutionA certain vector in the xy plane has an x-component of 12 m and a y-component of 8m. Its then rotated in the xy plane so that its x-component is halved. Then its new y-component is approximately :
View SolutionThe x and y-components of vector A are 4 m and 6 m respectively. The x and y-components of vector A + B are 10 m and 9 m respectively. Calculate for the vector B the following:
(a) its x and y-components
(b) its length
(c ) the angle it makes with x-axis.
View SolutionFind the resultant of the vectors shown in fig by the component method
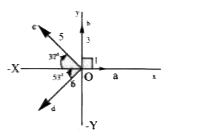
View SolutionFind the correct statement about the component of a vector is
View SolutionThere are two vectors →A=3ˆi+ˆj and →B=ˆj+2ˆk. For these two vectors-
(a) Find the component of →A along →B in vector form.
(b) If →A&→B are the adjacent sides of a parallalogram then find the magnitude of its area.
(c) Find a unit vector which is perpendicular to both →A&→B.
View SolutionA vector →F1 is along the positive X-axis. If its vectors product with another vector →F2 is zero then →F2 could be
View SolutionThe vertical component of a vector is equal to its horizontal component. What is the angle made by the vector with x-axis ?
View Solution
