The work done by a weightless piston in causing an expansing ΔV (at constant temperature), when the opposing pressure P is variable, is given by :
W=−∫pΔV
W = 0
W=−PΔV
None
The correct Answer is:A
To solve the question regarding the work done by a weightless piston during an expansion at constant temperature with variable opposing pressure, we can follow these steps:
1. Understanding Work Done by a Piston:
The work done W by a piston in a thermodynamic process can be expressed as the integral of pressure P with respect to volume V. The general formula for work done is:
W=−∫V2V1PdV
where V1 is the initial volume and V2 is the final volume.
2. Expressing Change in Volume:
The change in volume ΔV is defined as:
ΔV=V2−V1
Therefore, we can rewrite the work done in terms of ΔV:
W=−∫V2V1PdV=−PΔV
Here, we assume that P is the average pressure during the expansion.
3. Considering Constant Temperature:
Since the process occurs at constant temperature, we can assume that the gas behaves ideally. However, the pressure P is variable, so we cannot simplify it further without additional information about how P changes with V.
4. Final Expression for Work Done:
The final expression for the work done by the weightless piston during the expansion at constant temperature is:
W=−PΔV
This indicates that the work done by the system (the gas) is negative since the system is expanding against an external pressure.
5. Evaluating the Options:
- Option A: W=−PΔV (Correct)
- Option B: W=0 (Incorrect, as work is done)
- Option C: W=−PΔV (Incorrect, lacks the integral)
- Option D: None (Incorrect, since we have a correct answer)
Conclusion:
The correct answer is Option A: W=−PΔV.
The work done W by a piston in a thermodynamic process can be expressed as the integral of pressure P with respect to volume V. The general formula for work done is:
W=−∫V2V1PdV
where V1 is the initial volume and V2 is the final volume.
The change in volume ΔV is defined as:
ΔV=V2−V1
Therefore, we can rewrite the work done in terms of ΔV:
W=−∫V2V1PdV=−PΔV
Here, we assume that P is the average pressure during the expansion.
Since the process occurs at constant temperature, we can assume that the gas behaves ideally. However, the pressure P is variable, so we cannot simplify it further without additional information about how P changes with V.
The final expression for the work done by the weightless piston during the expansion at constant temperature is:
W=−PΔV
This indicates that the work done by the system (the gas) is negative since the system is expanding against an external pressure.
- Option A: W=−PΔV (Correct)
- Option B: W=0 (Incorrect, as work is done)
- Option C: W=−PΔV (Incorrect, lacks the integral)
- Option D: None (Incorrect, since we have a correct answer)
The correct answer is Option A: W=−PΔV.
Topper's Solved these Questions
- THERMODYNAMICS BOOK - ALLENCHAPTER - THERMODYNAMICS EXERCISE - EXERCISE -3
108 Videos
- THERMODYNAMICS BOOK - ALLENCHAPTER - THERMODYNAMICS EXERCISE - EXERCISE -4
18 Videos
- THERMODYNAMICS BOOK - ALLENCHAPTER - THERMODYNAMICS EXERCISE - EXERCISE -1B
22 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - MATHEMATICS
2 Videos
- Thermodynamics And Thermo ChemistryBOOK - ALLENCHAPTER - Thermodynamics And Thermo ChemistryEXERCISE - All Questions
40 Videos
Similar Questions
On doubling P and V at constant temperature, the equilibrium constant will
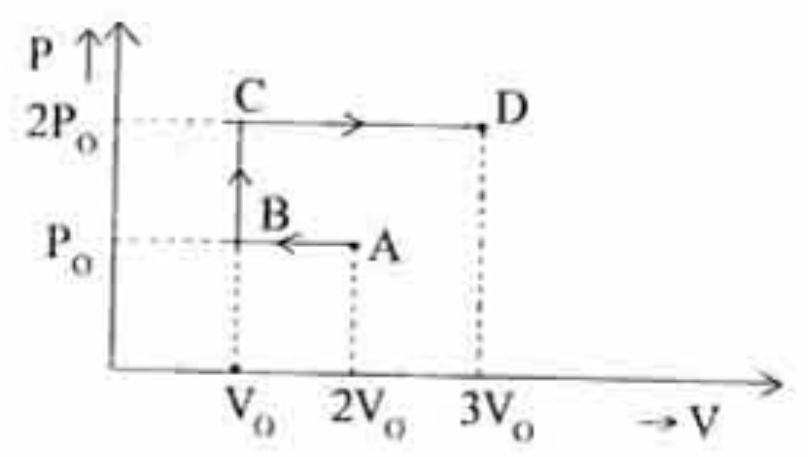
View SolutionThe work done by the gas in the process shown in given P-V diagram is
View SolutionGraph between speed v of sound in air and pressure P at a constant temperature is given by
View SolutionThe work done by one mole of ideal gas when its teperature is increased by 1oC at constant pressure is
View SolutionThe initial state of a certain gas is (pi,Vi,Ti). It undergoes explansion till its volume becomes Vf. Consider the following two cases
(a) the expansion takes place at constant temperature.
(b) the expansion takes place at constant pressure.
Plot the p−V diagram for each case. In which of the two cases, is the work done by the gas more ?
View SolutionWork done in reversible isothermal expansion is given by
View SolutionStatementI: Work done by a gas in isothermal expansion is more than the work done by the gas in the same expansion adaibatically.
Statement II: Temperature remains constant in isothermal ecpansion but not in adiabatic expansion.
View SolutionA quantity of gas occupies an initial volume V0 at pressure p0 and temperature T0. It expands to a volume V (a) constant temperature and (b) constant pressure. In which case does the gas do more work ?

View SolutionWhat will be the work done on an ideal gas enclosed in a cyliner, when it is compressed by a constant external pressure, pext in a single step as shown in figure ? Explain graphically.

View SolutionOne mole of a gas is put under a weightless piston of a vertical cylinder at temperature T. The space over the piston opens into atmosphere. Initially, piston was in equilibrium. How much work should be performed by some external force to increase isothermally the volume under the piston to twice the volume? (Neglect friction of piston).
View Solution
