Following curve shows the variation of intesity of gravitational field (→I) with distance from the centre of solid sphere(r) :
(a) 
(b) 
(c) 
(d) 
The correct Answer is:A
To solve the problem of the variation of gravitational field intensity with distance from the center of a solid sphere, we need to analyze two cases: when the distance r is greater than the radius of the sphere R and when r is less than R.
Step 1: Analyze the case when r>R (Outside the sphere)
1. When we are outside the solid sphere, we can treat the entire mass M of the sphere as if it were concentrated at a point at its center.
2. The gravitational field intensity →I at a distance r from the center is given by the formula:
→I=−GMr2^r
where G is the gravitational constant, M is the mass of the sphere, and ^r is the unit vector pointing away from the center.
Step 2: Analyze the case when r<R (Inside the sphere)
1. Inside the sphere, the gravitational field intensity depends on the mass enclosed within a radius r.
2. The mass M′ enclosed within radius r can be calculated using the ratio of volumes:
M43πR3=M′43πr3
This leads to:
M′=M⋅r3R3
3. The gravitational field intensity →I at a distance r from the center is then given by:
→I=−GM′r2^r=−G(M⋅r3R3)r2^r
Simplifying this gives:
→I=−GMR3r^r
This shows that the gravitational field intensity inside the sphere is directly proportional to r.
Step 3: Summary of the results
- For r>R:
→I∝1r2
- For r<R:
→I∝r
Conclusion
The variation of gravitational field intensity with distance from the center of the solid sphere shows that:
- Outside the sphere, the intensity decreases with the square of the distance.
- Inside the sphere, the intensity increases linearly with distance from the center.
2. The gravitational field intensity →I at a distance r from the center is given by the formula:
→I=−GMr2^r
where G is the gravitational constant, M is the mass of the sphere, and ^r is the unit vector pointing away from the center.
2. The mass M′ enclosed within radius r can be calculated using the ratio of volumes:
M43πR3=M′43πr3
This leads to:
M′=M⋅r3R3
3. The gravitational field intensity →I at a distance r from the center is then given by:
→I=−GM′r2^r=−G(M⋅r3R3)r2^r
Simplifying this gives:
→I=−GMR3r^r
This shows that the gravitational field intensity inside the sphere is directly proportional to r.
→I∝1r2
- For r<R:
→I∝r
- Outside the sphere, the intensity decreases with the square of the distance.
- Inside the sphere, the intensity increases linearly with distance from the center.
Topper's Solved these Questions
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 2
26 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 3
11 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - BOX-4
14 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective
14 Videos
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
46 Videos
Similar Questions
The diagram showing the variation of gravitational potential of earth with distance from the centre of earth is
View SolutionAn isolated solid metal sphere of radius R is given an electric charge. The variation of the intensity of the electric field with the distance r from the centre of the sphere is best shown by
View Solution
Knowledge Check
Which one of the following plots represents the variation of the gravitational field on a particle with distance r due to a thin spherical shell of raduis R? (r is measured from the centre of the spherical shell).
A B
B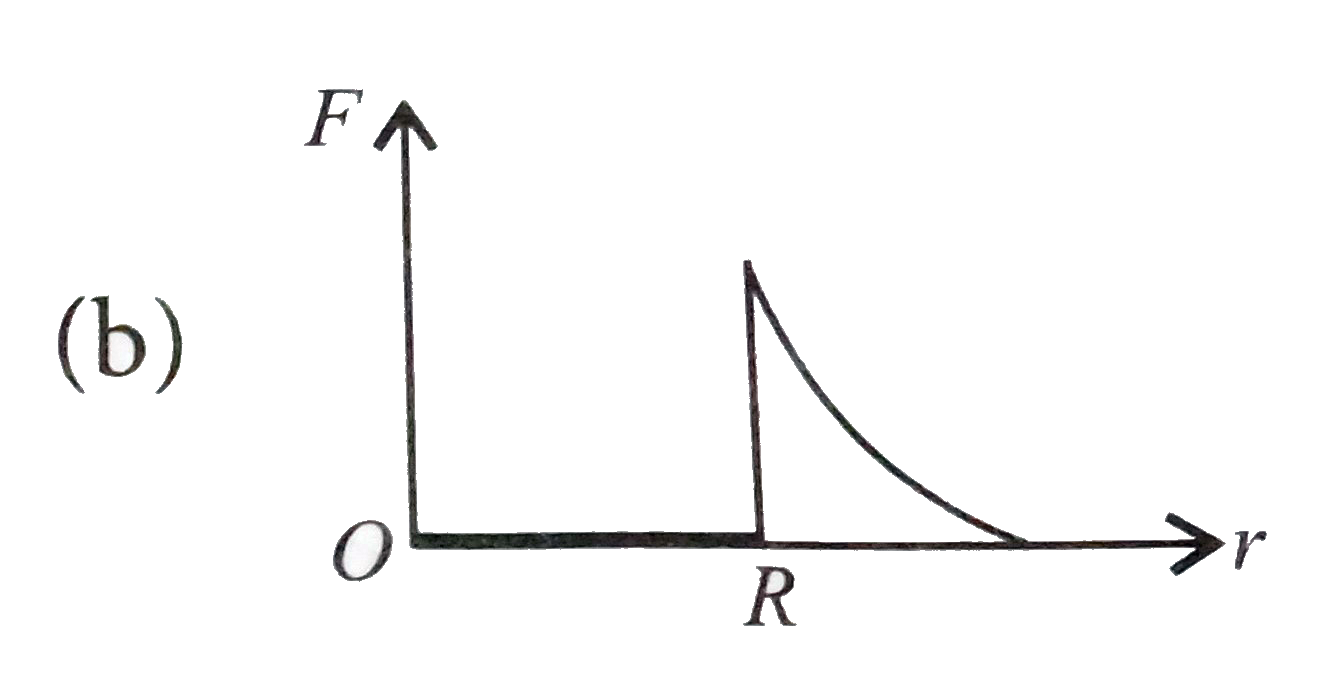 C
C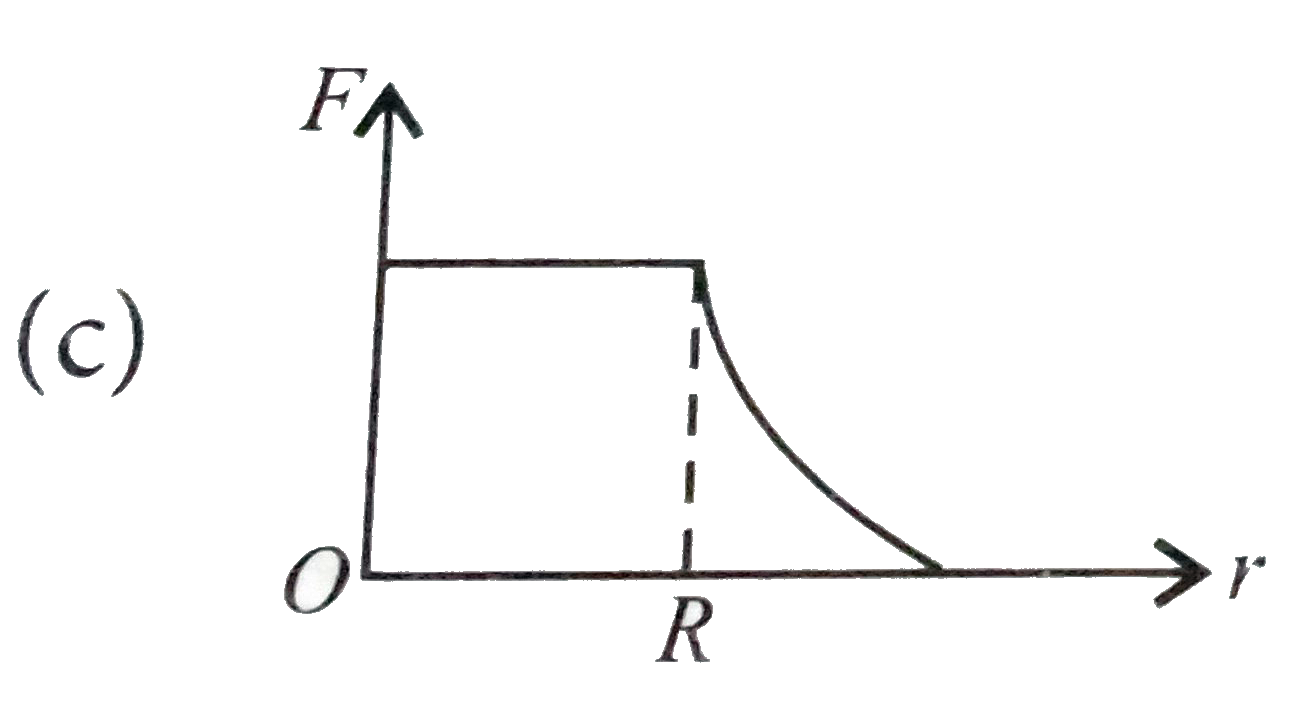 D
D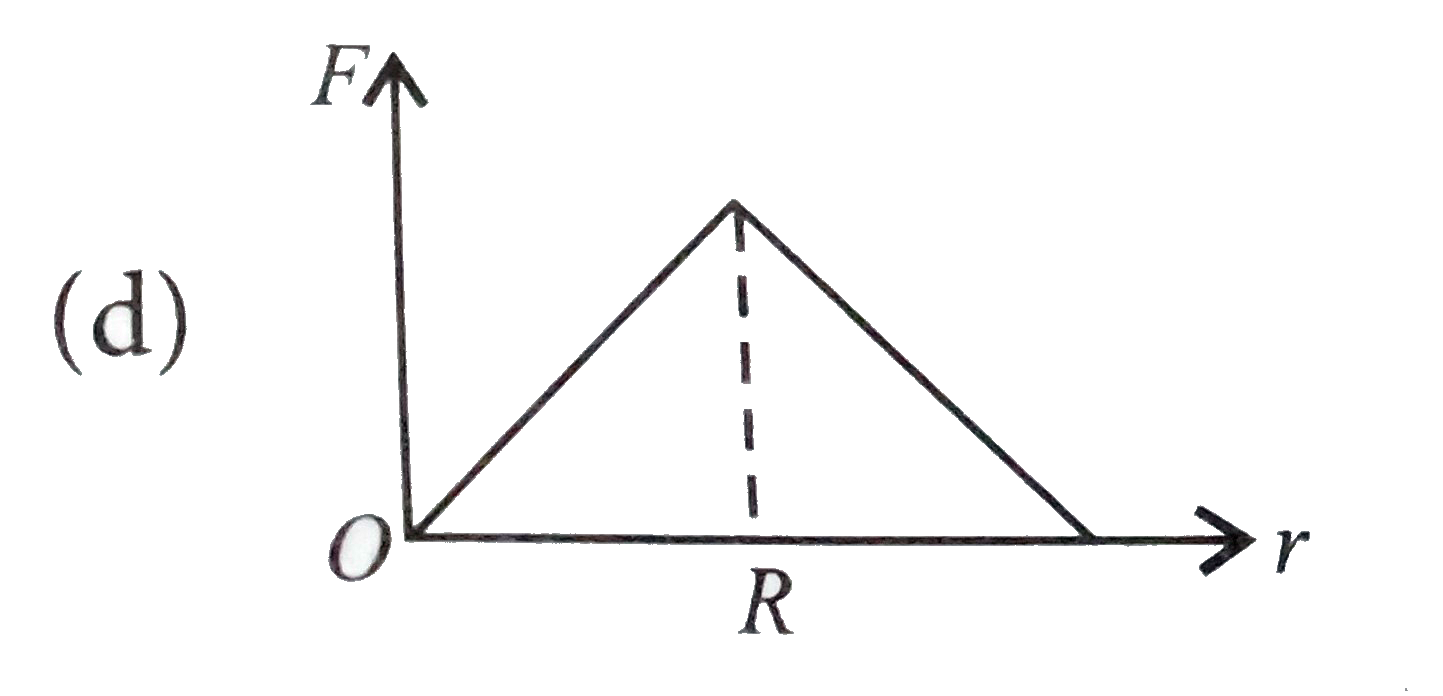
Dependence of intensity of gravitational field (E) of earth with distance (r) from centre of earth is correctly represented by
View SolutionDependence of intensity of gravitational field (E) of earth with distance (r) from centre of earth is correctly represented by
View SolutionWhich one of the following graphs represents the variation of electric field with distance r from the centre of a charged spherical conductor of radius R?
View SolutionGravitational field due to a solid sphere
View SolutionDraw a plot showing variation of electric field with distance from the centre of a solid conducting sphere of radius R, having of + Q on its surface.
View SolutionThe correct variation of gravitational potential V with radius r measured from the centre of earth of radius R is given by
View SolutionThe distance between the centres of the Moon and the earth is D. The mass of the earth is 81 times the mass of the Moon. At what distance from the centre of the earth, the gravitational force will be zero?
View Solution
