Question

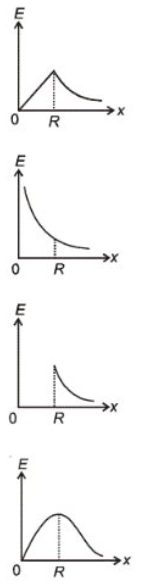
An isolated solid metal sphere of radius $R$ is
given an electric charge. The variation of the
intensity of the electric field with the distance
$r$ from the centre of the sphere is best shown
by

Options

A.
B.
C.
D.

Answer

C

Explanation

To solve the problem regarding the variation of the electric field intensity with distance from the center of an isolated solid metal sphere of radius $$R$$ that is given an electric charge, we can follow these steps:

1. Understanding the Sphere's Properties:
- An isolated solid metal sphere, when given a charge \( Q \), will have its charge distributed uniformly on its surface.

2. Electric Field Inside the Sphere:
- For any point inside the sphere (where \( r < R \)), the electric field intensity \( E \) is zero. This is because the electric field inside a conductor in electrostatic equilibrium is always zero.

\( E = 0 \quad \text{for} \quad r < R \)

3. Electric Field on the Surface of the Sphere:
- At the surface of the sphere (where \( r = R \)), we can calculate the electric field using Gauss's Law. The electric field intensity \( E \) at the surface is given by:

\( E = \frac{1}{4\pi \epsilon_0} \frac{Q}{R^2} \)

This value is the maximum electric field intensity for the sphere.

4. Electric Field Outside the Sphere:
- For points outside the sphere (where \( r > R \)), the electric field intensity behaves as if all the charge were concentrated at a point at the center of the sphere. The formula for the electric field intensity at a distance \( r \) from the center is:

\( E = \frac{1}{4\pi \epsilon_0} \frac{Q}{r^2} \)

This shows that the electric field intensity decreases with the square of the distance from the center of the sphere.

5. Graphical Representation:
- The graph of electric field intensity \( E \) versus distance \( r \) will show:
- \( E = 0 \) for \( r < R \)
- A maximum value at \( r = R \)
- A decreasing curve for \( r > R \)

6. Conclusion:
- Therefore, the correct representation of the variation of electric field intensity with distance from the center of the sphere is best shown by a graph that starts at zero, reaches a maximum at the surface, and then decreases as you move further away.

Final Answer:
The correct option for the variation of the electric field intensity with distance \( r \) from the center of the sphere is represented by option 3 (as mentioned in the video).