Two solid spherical planets of equal radii R having masses 4M and 9M their centre are separated by a distance 6R. A projectile of mass m is sent from theplanet of mass 4 M towards the heavier planet. What is the distance r of the point from the lighter planet where the gravitational force on the projectille is zero ?
1.4 R
1.8 R
1.5 R
2.4 R
The correct Answer is:D
To solve the problem, we need to find the distance r from the lighter planet (mass 4M) where the gravitational force on the projectile (mass m) is zero.
1. Identify the Setup:
- We have two planets:
- Planet 1 (lighter) with mass 4M
- Planet 2 (heavier) with mass 9M
- The distance between the centers of the two planets is 6R.
2. Define the Variables:
- Let r be the distance from the lighter planet (mass 4M) to the point where the gravitational force on the projectile is zero.
- Therefore, the distance from the heavier planet (mass 9M) to this point will be 6R−r.
3. Write the Gravitational Forces:
- The gravitational force F1 exerted by the lighter planet on the projectile is given by:
F1=G⋅4M⋅mr2
- The gravitational force F2 exerted by the heavier planet on the projectile is given by:
F2=G⋅9M⋅m(6R−r)2
4. Set the Forces Equal:
- For the gravitational forces to balance (i.e., the net force on the projectile is zero), we set F1=F2:
G⋅4M⋅mr2=G⋅9M⋅m(6R−r)2
- We can cancel G, M, and m from both sides:
4r2=9(6R−r)2
5. Cross-Multiply:
- Cross-multiplying gives:
4(6R−r)2=9r2
6. Expand and Rearrange:
- Expanding the left side:
4(36R2−12Rr+r2)=9r2
144R2−48Rr+4r2=9r2
- Rearranging gives:
144R2−48Rr−5r2=0
7. Use the Quadratic Formula:
- This is a quadratic equation in terms of r:
5r2+48Rr−144R2=0
- Using the quadratic formula r=−b±√b2−4ac2a:
- Here, a=5, b=48R, and c=−144R2.
r=−48R±√(48R)2−4⋅5⋅(−144R2)2⋅5
r=−48R±√2304R2+2880R210
r=−48R±√5184R210
r=−48R±72R10
8. Calculate the Roots:
- This gives two potential solutions:
- r=24R10=2.4R (valid solution since it is positive)
- r=−120R10=−12R (not valid since distance cannot be negative)
9. Final Answer:
- Therefore, the distance r from the lighter planet where the gravitational force on the projectile is zero is:
r=2.4R
- We have two planets:
- Planet 1 (lighter) with mass 4M
- Planet 2 (heavier) with mass 9M
- The distance between the centers of the two planets is 6R.
- Let r be the distance from the lighter planet (mass 4M) to the point where the gravitational force on the projectile is zero.
- Therefore, the distance from the heavier planet (mass 9M) to this point will be 6R−r.
- The gravitational force F1 exerted by the lighter planet on the projectile is given by:
F1=G⋅4M⋅mr2
- The gravitational force F2 exerted by the heavier planet on the projectile is given by:
F2=G⋅9M⋅m(6R−r)2
- For the gravitational forces to balance (i.e., the net force on the projectile is zero), we set F1=F2:
G⋅4M⋅mr2=G⋅9M⋅m(6R−r)2
- We can cancel G, M, and m from both sides:
4r2=9(6R−r)2
- Cross-multiplying gives:
4(6R−r)2=9r2
- Expanding the left side:
4(36R2−12Rr+r2)=9r2
144R2−48Rr+4r2=9r2
- Rearranging gives:
144R2−48Rr−5r2=0
- This is a quadratic equation in terms of r:
5r2+48Rr−144R2=0
- Using the quadratic formula r=−b±√b2−4ac2a:
- Here, a=5, b=48R, and c=−144R2.
r=−48R±√(48R)2−4⋅5⋅(−144R2)2⋅5
r=−48R±√2304R2+2880R210
r=−48R±√5184R210
r=−48R±72R10
- This gives two potential solutions:
- r=24R10=2.4R (valid solution since it is positive)
- r=−120R10=−12R (not valid since distance cannot be negative)
- Therefore, the distance r from the lighter planet where the gravitational force on the projectile is zero is:
r=2.4R
Topper's Solved these Questions
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 2
26 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective
14 Videos
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
46 Videos
Similar Questions
Two particles A and B having masses M and 4M respectively are kept at a distance 2.73 m apart. Another small particle of mass m is to be placed so that the net gravitational force on it is zero. What will be its distance from body A ?
View SolutionTwo point masses m and 4 m are seperated by a distance d on a line . A third point mass m0 is to be placed at a point on the line such that the net gravitational force on it zero .

The distance of that point from the m mass is
View Solution
Knowledge Check
Two identical spheres each of mass M and Radius R are separated by a distance 10R. The gravitational force on mass m placed at the midpoint of the line joining the centres of the spheres is
AzeroB2GMm25R2CGMm25R2DGMm100R2Two uniform solid spheres of equal radii R, but mass M and 4 M have a centre to centre separation 6 R, as shown in figure. The two spheres are held fixed. A projectile of mass m is projected from the surface of the sphere of mass M directly towards the centre of the second sphere. Obtain an expression for the minimum speed v of the projectile so that it reaches the surface of the second sphere.
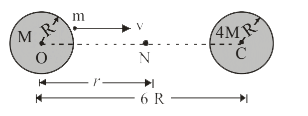 A√45GMRB√54GMRC√35GMRD√53GMR
A√45GMRB√54GMRC√35GMRD√53GMR
Two point masses having mass m and 2m are placed at distance d . The point on the line joining point masses , where gravitational field intensity is zero will be at distance
View SolutionTwo uniform soild spheres of equal radii R but mass M and 4M have a centre to centre separation 6R, as shows in Fig. (a) The two spheres are held fixed. A projectile of massm is projected from the surface of the sphere of mass M directly towards the centre of teh second. Obtain an expression for the minimum speed υ of the projectile so that it reaches the surface of second sphere.
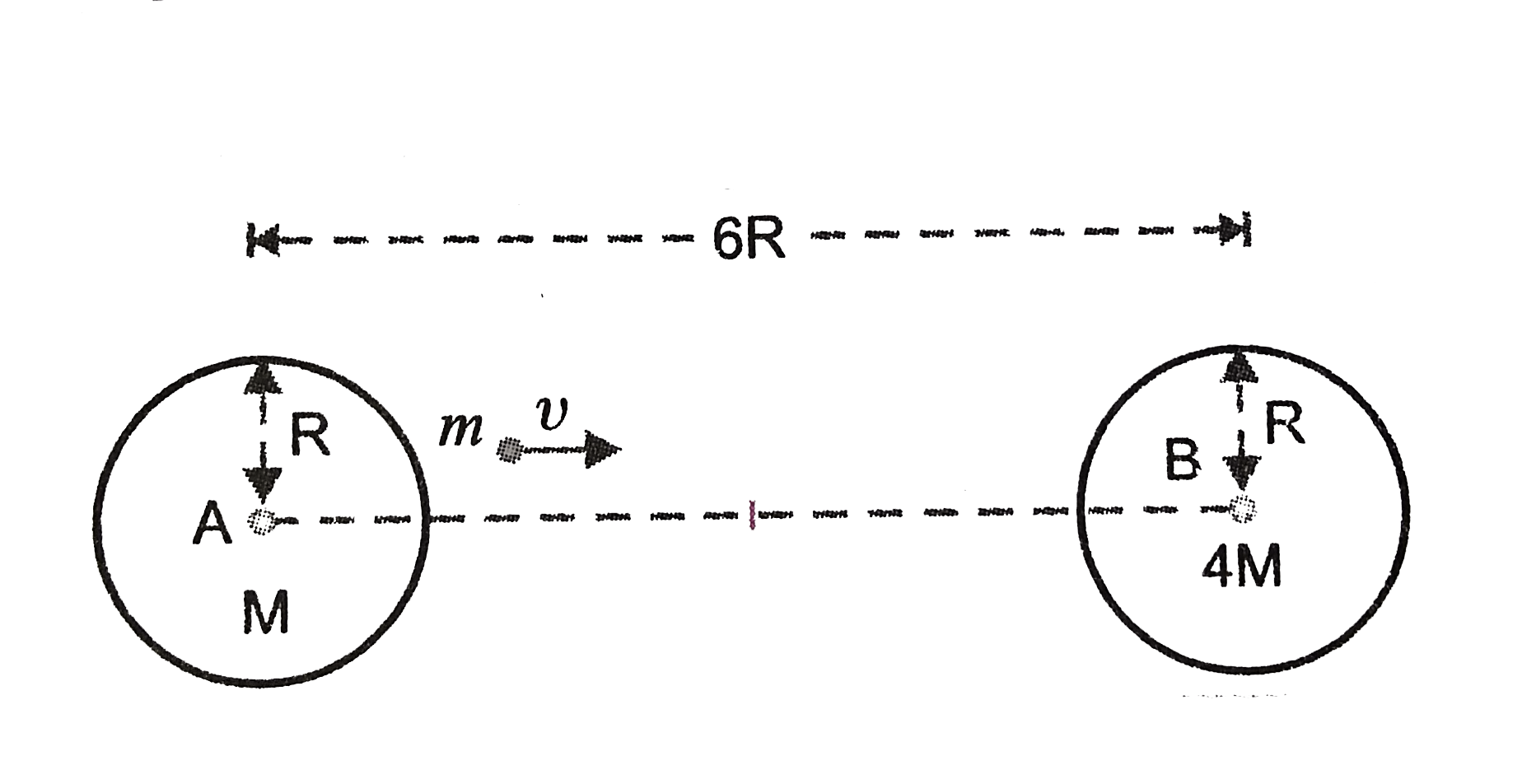
View SolutionTwo bodies of masses m and 4m are placed at a distance r. The gravitational potential at a point due to mass m on the line joining where gravitational field is zero
View SolutionA satellite A of mass m is at a distance of r from the centre of the earth. Another satellite B of mass 2m is at distance of 2r from the earth's centre. Their time periode are in the ratio of
View SolutionThe figure represents a solid uniform sphere of mass M and radius R. A spherical cavity of radius r is at a distance a from the centre of the sphere. The gravitational field inside the cavity is

View SolutionA solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distance R/4 from the centre of sphere. The gravitational force on mass m is
View Solution
