Resultant of two forces →F1 and →F2 has magnitude 50 N. The resultant is inclined to →F1 at 60∘ and to →F1 at 30∘ . Magnitudes of →F1 and →F2, respectively, are:
25 N, 25√3N
20 N, 20√3N
20 N, 30N
30 N, 40N
The correct Answer is:A
To solve the problem, we need to find the magnitudes of the forces →F1 and →F2 given that the resultant force has a magnitude of 50 N and is inclined at angles of 60° and 30° to →F1 and →F2 respectively.
1. Understanding the Geometry:
- We have two forces →F1 and →F2.
- The resultant →R has a magnitude of 50 N.
- The angle between →R and →F1 is 60°.
- The angle between →R and →F2 is 30°.
2. Using the Cosine Rule:
- From the geometry of the triangle formed by →F1, →F2, and →R, we can use the cosine of the angles to find the components of the forces.
- For →F1:
cos(60°)=F1R
Substituting R=50:
cos(60°)=F150
Since cos(60°)=12:
12=F150
Therefore, multiplying both sides by 50:
F1=50×12=25 N
3. Finding →F2:
- Now, for →F2:
cos(30°)=F2R
Substituting R=50:
cos(30°)=F250
Since cos(30°)=√32:
√32=F250
Therefore, multiplying both sides by 50:
F2=50×√32=25√3 N
4. Final Result:
- The magnitudes of the forces →F1 and →F2 are:
F1=25 N,F2=25√3 N
Summary of Results:
- The magnitudes of →F1 and →F2 are 25 N and 25√3 N respectively.
- We have two forces →F1 and →F2.
- The resultant →R has a magnitude of 50 N.
- The angle between →R and →F1 is 60°.
- The angle between →R and →F2 is 30°.
- From the geometry of the triangle formed by →F1, →F2, and →R, we can use the cosine of the angles to find the components of the forces.
- For →F1:
cos(60°)=F1R
Substituting R=50:
cos(60°)=F150
Since cos(60°)=12:
12=F150
Therefore, multiplying both sides by 50:
F1=50×12=25 N
- Now, for →F2:
cos(30°)=F2R
Substituting R=50:
cos(30°)=F250
Since cos(30°)=√32:
√32=F250
Therefore, multiplying both sides by 50:
F2=50×√32=25√3 N
- The magnitudes of the forces →F1 and →F2 are:
F1=25 N,F2=25√3 N
- The magnitudes of →F1 and →F2 are 25 N and 25√3 N respectively.
Topper's Solved these Questions
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Units, Dimensions & Measurements)
30 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (KINEMATICS)
59 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Co-ordinate & Algebra)
37 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Video
Similar Questions
The resultant of the forces →F1=4ˆi−3ˆj and →F2=6ˆi+8ˆj is
View SolutionConsider two vectors →F1=2ˆi+5ˆk and →F2=3ˆj+4ˆk. The magnitude to thhe scalar product of these vectors is
View SolutionTwo forces →F1=(3N)ˆi−(4N)ˆj and →F2=−(1N)ˆi−(2N)ˆj act on a point object. In the given figure which of the six vectors represents →F1 and →F2 and what is the magnitude of the net forces

View SolutionA vector →F1 is along the positive X-axis. If its vectors product with another vector →F2 is zero then →F2 could be
View SolutionTwo constant forces →F1 and →F2 act on a body of mass 8kg. These forces displace the body from point P(1,−2,3) to Q (2,3,7) in 2s starting from rest. Force →F1 is of magnitude 9N and is acting along vector (2ˆi−2ˆj+ˆk). Work done by the force →F2 is
View SolutionA particle with a mass of 1kg a velocity of is having 10m/s in +vex-direction at t=0. Forces →F1 and →F2, act on the particle whose magnitudes are changing with time according to the variation shown in Fig. The magnitude of the velocity of the particle at t=3s (neglect gravity effect) is found to be n√5 Find the value of n
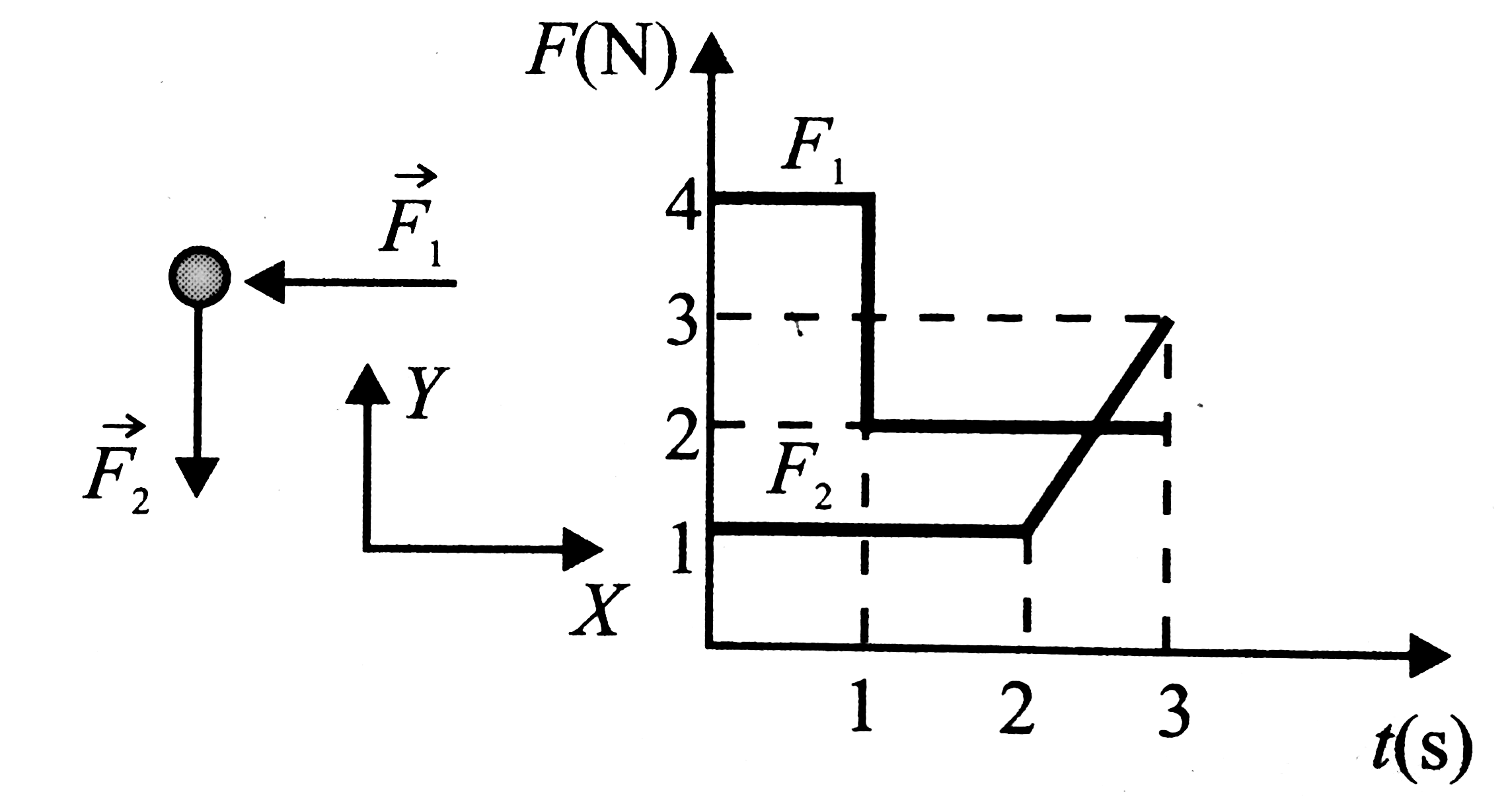
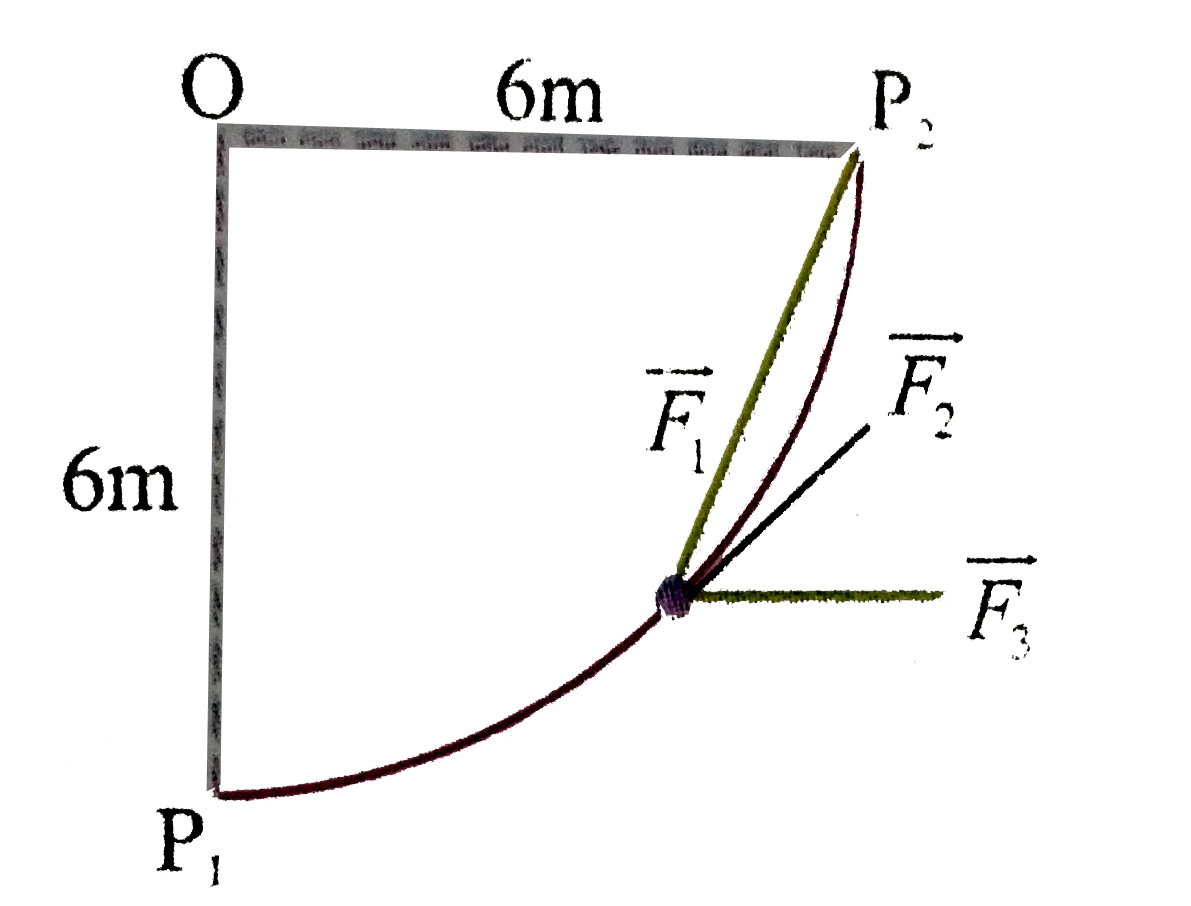
View SolutionA smooth track in the form of a quarter circle of radius 6m lies in the vertical plane. A particle moves from P1 to P2 under the action of forces →F1,→F2 and →F3 Force →F1 is always 30N in magnitude. Force →F3 always acts tangentiallly to the track and is of magnitude 15N. Select the correct alternative (s) :
 .
.
View SolutionA vector →F1 is along the positive X-axis. its vectors product with another vector →F2 is ? where →F2 is along Y-axis
View SolutionA particle moves in a circle with a uniform speed. When it goes from a point A to a diametrically opposite point B, the momentum of the particle changes by →PA−→PB=2 kg m/s (ˆj) and the centripetal force acting on it changes by →FA−→FB=8N(ˆi) where ˆi,ˆj are unit vectors along X and Y axes respectively. The angular velocity of the particle is
View SolutionThe base vectors →a1,→a2 and →a3 are given in terms of base vectors →b1,→b2 and →b3 as →a1=2→b1+3→b2−→b3, →a2=→b1−2→b2+2→b3 and →a3=2→b1+→b2−2→b3, if →F=3→b1−→b2+2→b3, then vector →F in terms of →a1,→a2 and →a3 is
View Solution
