Block a of mass 4 kg is to be kept at rest against a smooth vertical wall by applying a force F as shown in figure. The force required is :- (g=10m/s2)
40√2N
20√2N
10√2N
15√2N
The correct Answer is:A
To solve the problem of keeping block A of mass 4 kg at rest against a smooth vertical wall by applying a force F, we will follow these steps:
Step 1: Identify the forces acting on the block
The forces acting on block A are:
1. The gravitational force (weight) acting downwards, mg.
2. The applied force F at an angle of 45 degrees to the horizontal.
Step 2: Calculate the weight of the block
Given:
- Mass of the block, m=4kg
- Acceleration due to gravity, g=10m/s2
The weight of the block is calculated as:
mg=4kg×10m/s2=40N
Step 3: Set up the equilibrium condition
Since the block is at rest, the net force acting on it must be zero. We will analyze the vertical forces. The vertical component of the applied force F must balance the weight of the block.
The vertical component of the force F can be expressed as:
Fy=Fsin(45∘)
For equilibrium in the vertical direction:
Fy=mg
Substituting the values:
Fsin(45∘)=40N
Step 4: Solve for the applied force F
We know that sin(45∘)=√22. Substituting this into the equation gives:
F⋅√22=40
To isolate F, we multiply both sides by 2√2:
F=40⋅2√2=40√2N
Conclusion
The force required to keep block A at rest against the wall is:
F=40√2N
Final Answer
The correct answer is 40√2N.
---
The forces acting on block A are:
1. The gravitational force (weight) acting downwards, mg.
2. The applied force F at an angle of 45 degrees to the horizontal.
Given:
- Mass of the block, m=4kg
- Acceleration due to gravity, g=10m/s2
mg=4kg×10m/s2=40N
Since the block is at rest, the net force acting on it must be zero. We will analyze the vertical forces. The vertical component of the applied force F must balance the weight of the block.
Fy=Fsin(45∘)
Fy=mg
Substituting the values:
Fsin(45∘)=40N
We know that sin(45∘)=√22. Substituting this into the equation gives:
F⋅√22=40
F=40⋅2√2=40√2N
The force required to keep block A at rest against the wall is:
F=40√2N
The correct answer is 40√2N.
Topper's Solved these Questions
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (FRICTION)
14 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (WORK POWER & ENERGY)
34 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (KINEMATICS)
59 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
Similar Questions
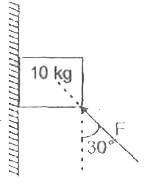
A block of mass 10 kg is held at rest against a rough vertical wall [μ=0.5] under the action a force F as shown in figure. The minimum value of F required for it is (g=10m/s2)
View SolutionA cubical block of side 'a' is held at rest, against a rough vertical wall by applying a force F acting along the centre. The mass of the block is m. Taking acceleration due to gravity as 'g' , determine
(i) The minimum coefficient of friction between the block and wall
(ii) The torque by normal reaction about the centre of mass
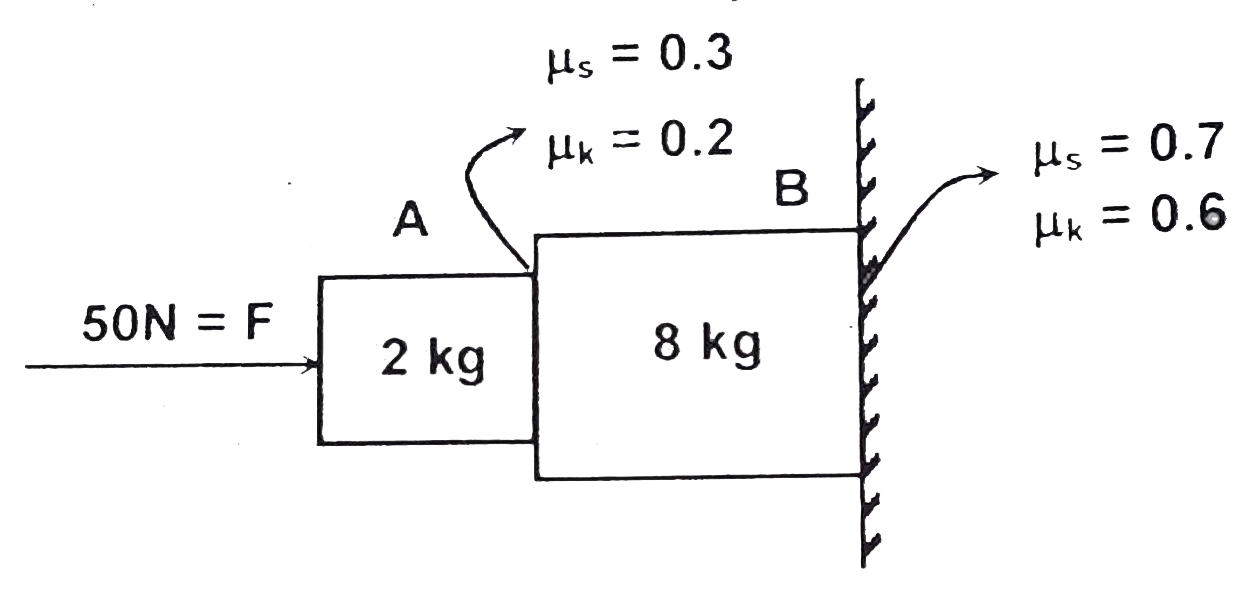
View SolutionTwo blocks A and B of masses 2kg and 8kg respectively are kept in contact and pressed against a roguh vertical wall by applying a horizontal force F=50N as shown, The frictional force acting between the two blocks is
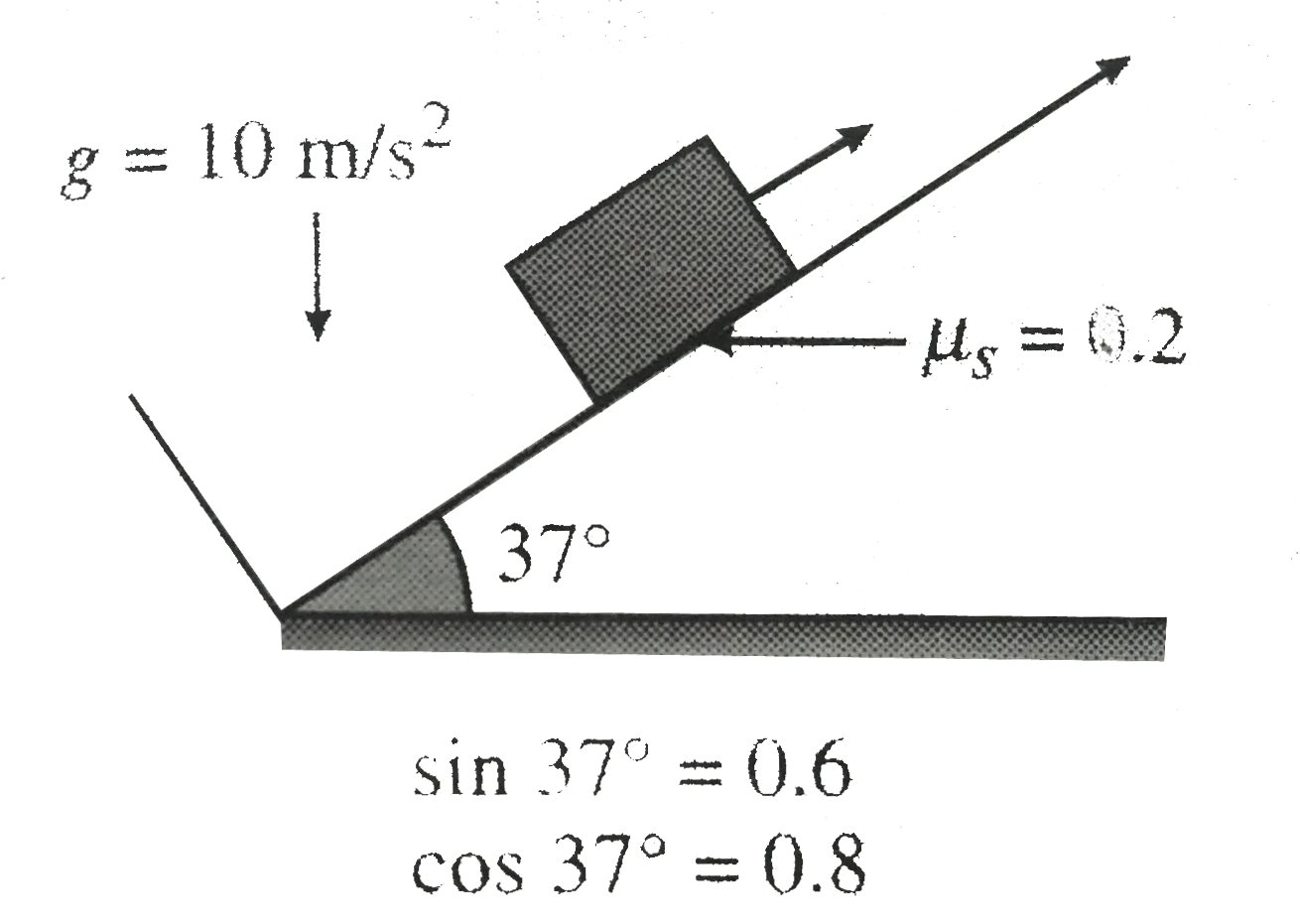
View SolutionAn object of mass 10kg is to be kept at rest on an inclined plane making an angle of 37∘to the horizontal by applying a force F along the plane upwards as shown in figure . The coefficient of static fiction between the object and the plane is 0.2 Find the magnitude of force F
[Take g=10ms−2]
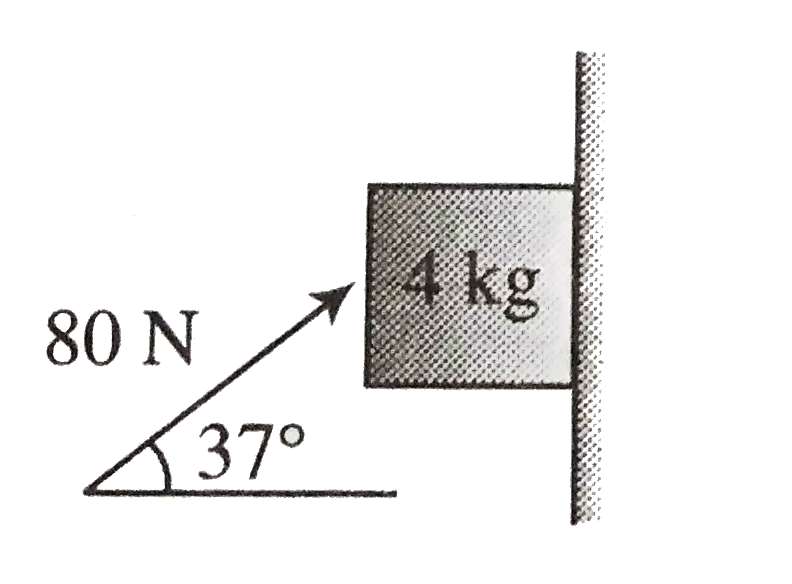
View SolutionA block of mass 4kg is pressed againest the wall by a force of 80N as shown in figure Determine the value of the friction force and block's acceleration (Take μs=0.2,μs=0.15)
View SolutionA block of mass 20 kg is on a horizontal plane of a coefficient of friction 0.5. by applying 6.0 newton force on it, frictional force will be (g=10m/s2).
View SolutionA block A is held at rest against a smooth wall by application of force at p. The direction of force at P. the direction of force to be applied at P.

View SolutionA block of mass m is at rest under the action of force F against a wall as shown in figure. Which of the following statement is incorrect?
View SolutionA block weighs W is held against a vertical wall by applying a horizontal force F. The minimum value of F needed to hold the block is
View SolutionA block of 1 kg is stopped against a wall by applying a force F perpendicular to the wall. If μ=0.2 then minimum value of F will be
View Solution
