What is the maximum value of force, so that both the blocks will move together ?
The correct Answer is:403N
To solve the problem of finding the maximum value of force F so that both blocks move together, we can follow these steps:
Step 1: Identify the Given Values
We have two blocks with the following properties:
- Mass of block 1 (m1) = 2 kg
- Mass of block 2 (m2) = 3 kg
- Coefficient of friction for block 1 (μ1) = 0.2
- Coefficient of friction for block 2 (μ2) = 0.6
- Acceleration due to gravity (g) = 9.8 m/s² (assuming standard value)
Step 2: Calculate the Maximum Static Friction Forces
The maximum static friction force for each block can be calculated using the formula:
fmax=μ⋅m⋅g
For block 1:
f1=μ1⋅m1⋅g=0.2⋅2⋅9.8=3.92N
For block 2:
f2=μ2⋅m2⋅g=0.6⋅3⋅9.8=17.64N
Step 3: Set Up the Equations of Motion
When both blocks are moving together, the force F must overcome the friction acting on both blocks. The total friction force opposing the motion is the sum of the friction forces acting on both blocks:
Ffriction=f1+f2=3.92+17.64=21.56N
Step 4: Apply Newton's Second Law
For both blocks to move together, the applied force F must equal the total friction force:
F=f1+f2
Step 5: Calculate the Maximum Force
Thus, the maximum force F that can be applied so that both blocks move together is:
F=21.56N
Conclusion
The maximum value of force F so that both blocks will move together is approximately 21.56 N.
---
We have two blocks with the following properties:
- Mass of block 1 (m1) = 2 kg
- Mass of block 2 (m2) = 3 kg
- Coefficient of friction for block 1 (μ1) = 0.2
- Coefficient of friction for block 2 (μ2) = 0.6
- Acceleration due to gravity (g) = 9.8 m/s² (assuming standard value)
The maximum static friction force for each block can be calculated using the formula:
fmax=μ⋅m⋅g
f1=μ1⋅m1⋅g=0.2⋅2⋅9.8=3.92N
f2=μ2⋅m2⋅g=0.6⋅3⋅9.8=17.64N
When both blocks are moving together, the force F must overcome the friction acting on both blocks. The total friction force opposing the motion is the sum of the friction forces acting on both blocks:
Ffriction=f1+f2=3.92+17.64=21.56N
For both blocks to move together, the applied force F must equal the total friction force:
F=f1+f2
Thus, the maximum force F that can be applied so that both blocks move together is:
F=21.56N
The maximum value of force F so that both blocks will move together is approximately 21.56 N.
Topper's Solved these Questions
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (WORK POWER & ENERGY)
34 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (CIRCULAR MOTION)
17 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (NEWTONS LAWS OF MOTION)
46 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
Similar Questions
Two block , with masses m1 and m2 are staked as shown in fig and placed on a frictionless horizontal surface . There is a friction between the two block .An external force of magnitude F is applied to the top block at an angle α below the horizontal . The coefficient of friction between m1 and m2 are μs
b. If the two blocks move together, find their acceleration
b . Calculate the maximum value of force so that blocks will move together

View SolutionThere are two block as shown in the figure of masses 1kg and 4kg. Friction coefficient between any two surfaces are 0.2 then find maximum value of horizontal force F so that both blocks moves together.
_2019_CBT6_E01_036_Q01.png)
View Solution
Knowledge Check
What is the maximum value of the force F such that the block shown in the arrangement, does not move?
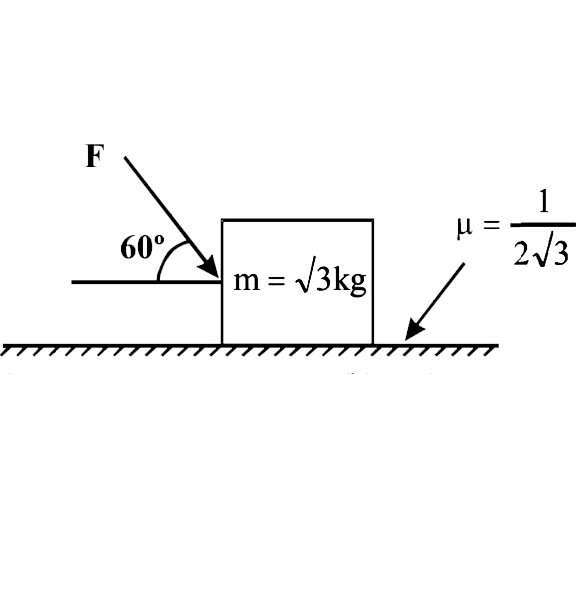 A20NB10NC12ND15N
A20NB10NC12ND15N

What is the minimum value of applied force F so that both the block lifts up. Consider string to be ideal. The mass of pulley P1 is 6 kg and pulley P2 is light.
View SolutionWhat is the maximum value of the force F such that the block shown in the figure does not move?

View SolutionWhat is the maximum value of the force F such that the block shown in the arrangement, does not move:
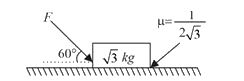
View SolutionIn the sitution shown in figure there is no friction between 2kg and ground.

a. For what maximum value of force F can all three blocks move together?
b. Find the value of force F at which sliding starts at other rough surfaces.
c. Find acceleration of all blocks, nature and value of friction force for the following values of force F (i) 10N (ii) N and (iii) 25N
View SolutionThe coefficient of static friction, μs between block A mass 2kg and the table as shown in the figure, is 0.2. What would be the maximum mass value of block B, so that the two blocks do not move ? The string and the pulley are asseumed to be smooth and massless (g=10m/s2)

View SolutionThe coefficient of static friction, μs between block A of mass 2 kg and the table as shown in the figure is 0.2. What would be the maximum mass value of block B so that the two blocks do not move? The string and the pulley are assumed to be smooth and massless.(g=10m/s2)

View SolutionA block of mass 10 kg is kept on a rough inclined plane as shown in the figure. A force of 3 N is applied on the block. The coefficient of static friction between the plane and the block is 0.6 What should be the minimum value of force P, such that the block doesnot move downward? (take g=10ms−2)

View Solution
