There are two bodies A & B of same mass body A is at rest while body B is under going uniform motion, which is correct statements ?
Inertia of A>inertia of B.
Inertia of B> inertia of A.
Inertia of A = inertia of B.
Either 1st,2nd or 3rd depending upon the shape of body.
The correct Answer is:C
To solve the question, we need to analyze the concept of inertia and how it relates to the two bodies A and B.
1. Understanding the Concept of Inertia:
- Inertia is the property of an object to resist changes in its state of motion. It is directly related to the mass of the object. The greater the mass, the greater the inertia.
2. Identifying the Conditions of the Bodies:
- Body A is at rest, which means its velocity (V_A) is 0 m/s and it has no acceleration (a_A = 0).
- Body B is undergoing uniform motion, which means it has a constant velocity (V_B ≠ 0) and also has no acceleration (a_B = 0).
3. Comparing the Masses of the Bodies:
- The problem states that both bodies A and B have the same mass (m_A = m_B).
4. Relating Mass to Inertia:
- Since mass is a measure of inertia, we can conclude that:
- Inertia of body A (I_A) = mass of body A (m_A)
- Inertia of body B (I_B) = mass of body B (m_B)
5. Conclusion on Inertia:
- Since m_A = m_B, we can state that:
- I_A = I_B
- Therefore, the inertia of body A is equal to the inertia of body B.
6. Final Answer:
- The correct statement is that the inertia of A is equal to the inertia of B.
Correct Option:
- The correct option is C: Inertia of A is equal to inertia of B.
- Inertia is the property of an object to resist changes in its state of motion. It is directly related to the mass of the object. The greater the mass, the greater the inertia.
- Body A is at rest, which means its velocity (V_A) is 0 m/s and it has no acceleration (a_A = 0).
- Body B is undergoing uniform motion, which means it has a constant velocity (V_B ≠ 0) and also has no acceleration (a_B = 0).
- The problem states that both bodies A and B have the same mass (m_A = m_B).
- Since mass is a measure of inertia, we can conclude that:
- Inertia of body A (I_A) = mass of body A (m_A)
- Inertia of body B (I_B) = mass of body B (m_B)
- Since m_A = m_B, we can state that:
- I_A = I_B
- Therefore, the inertia of body A is equal to the inertia of body B.
- The correct statement is that the inertia of A is equal to the inertia of B.
- The correct option is C: Inertia of A is equal to inertia of B.
Topper's Solved these Questions
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (FRICTION)
14 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (WORK POWER & ENERGY)
34 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (KINEMATICS)
59 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
Similar Questions
Knowledge Check
The figure shows the variation of energy with the orbit radius of a body in circular planetary motion. Find the correct statements about the curves A,B and C
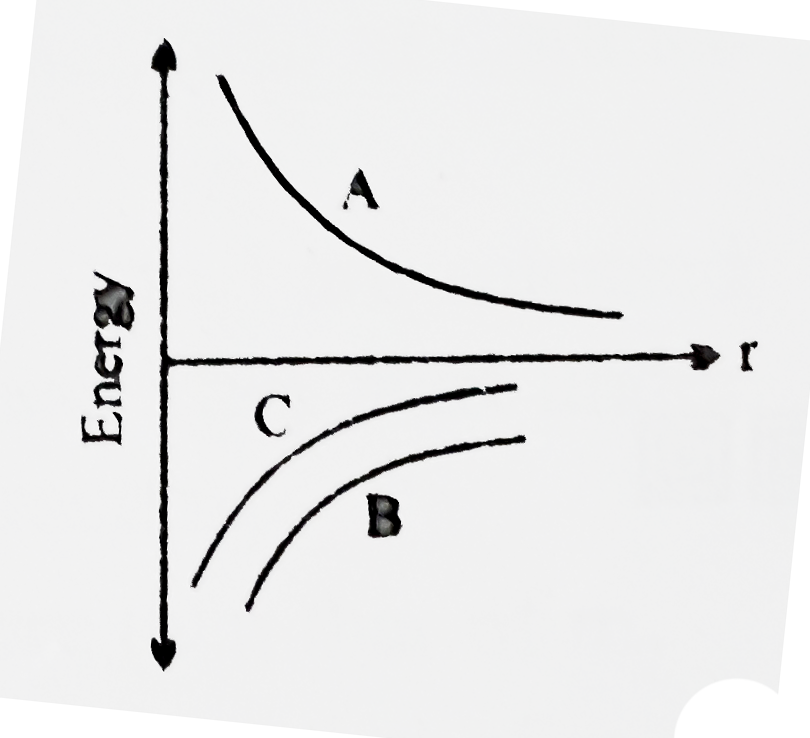 AA shows the kinetic energy, B shows the total energy and C the potential energy of the satelliteBA and b are kinetic energy and potential energy respectively and C the total energy of the satellite.CA and B are the potentital energy and kinetic energy respectively and C the total energy of the satellite .DC and A are the kinetic and potential energies and B the total energy of the satellite .
AA shows the kinetic energy, B shows the total energy and C the potential energy of the satelliteBA and b are kinetic energy and potential energy respectively and C the total energy of the satellite.CA and B are the potentital energy and kinetic energy respectively and C the total energy of the satellite .DC and A are the kinetic and potential energies and B the total energy of the satellite .
What is the average velocity of a body in uniform circular motion ?
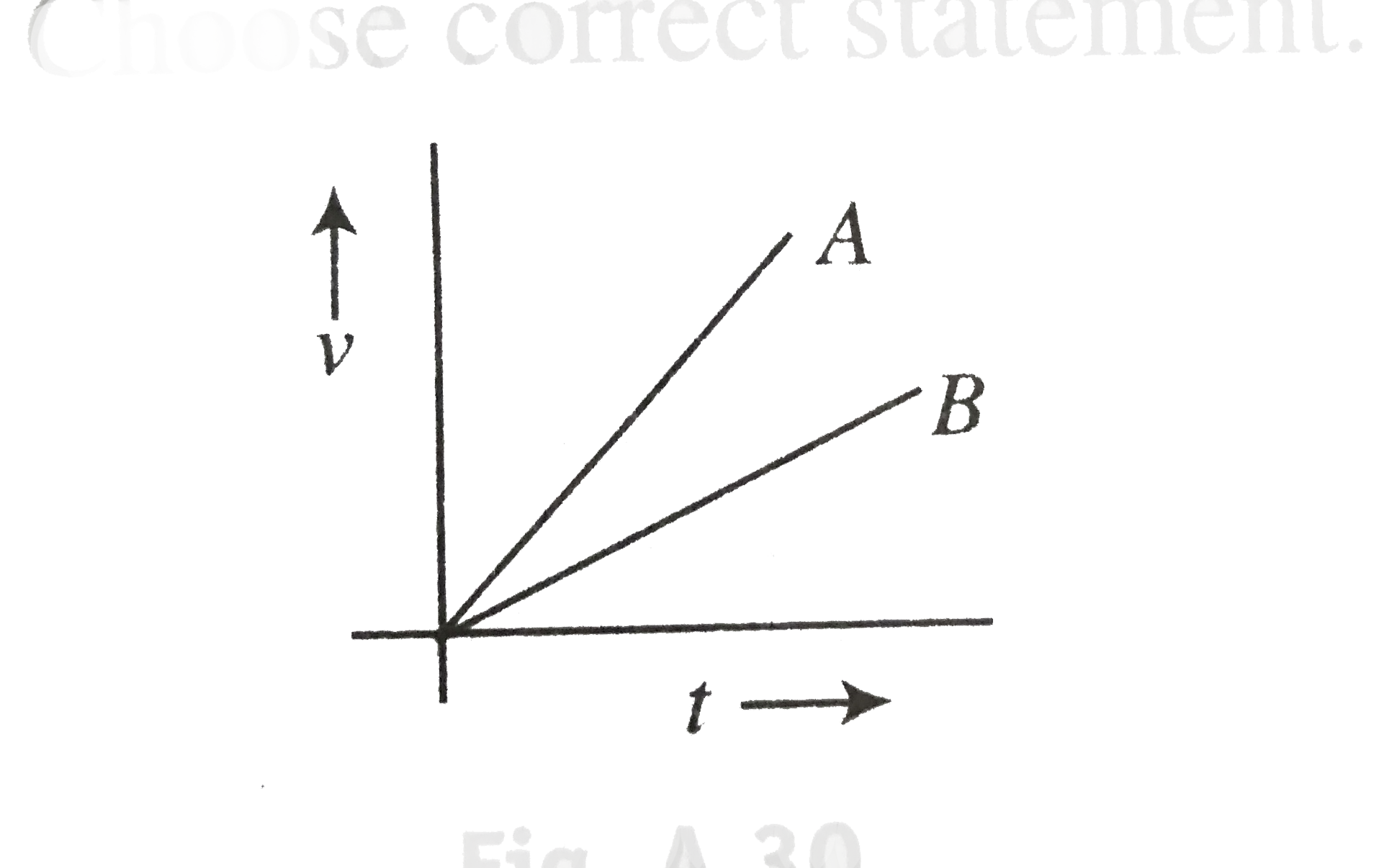
View SolutionThe velocity - time graph of two bodies A and B is shown in figure. Choose correct statement.
View SolutionIs a body in uniform circular motion in equilibrium ?
View SolutionHow do you determine the average speed of a body in non-uniform motion ?
View SolutionThe figure shows the variation of energy with the orbit radius of a body in circular planetary motion. Find the correct statements about the curves A,B and C

View SolutionA body starts from rest and then moves with uniform acceleration. Then.
View SolutionTwo bodies A and B of same mass are moving with velocities v and 2v, respectively. Compare their inertia
View Solution
