A particle of mass m is taken from position A to position B along the circular path by a constant horizontal force →F. What will be the work done by the force →F? Here radius of Track is R.
lmg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_R01_E06_010_Q01.png" width="80%"gt
a.FR
b.F(πR2)
F(√2R)
None
The correct Answer is:C
To find the work done by the constant horizontal force →F when moving a particle of mass m from position A to position B along a circular path of radius R, we can follow these steps:
Step 1: Understand the Motion
The particle moves along a circular path from point A to point B. The radius of the circular path is R.
Step 2: Identify the Displacement
As the particle moves from A to B, it rises vertically to a height equal to the radius R. Therefore, the vertical displacement h is R.
Step 3: Determine the Work Done Formula
The work done W by a force is given by the formula:
W=F⋅s⋅cos(θ)
where:
- F is the magnitude of the force,
- s is the displacement,
- θ is the angle between the force and the direction of displacement.
Step 4: Analyze the Angle
In this case, the force →F is applied horizontally, while the displacement in the vertical direction is R. Therefore, the angle θ between the force and the direction of displacement is 0∘ (since the force is horizontal and the displacement is vertical).
Step 5: Calculate the Work Done
Since the angle θ=0∘, we have:
cos(0∘)=1
Thus, the work done can be simplified to:
W=F⋅R⋅1=F⋅R
Conclusion
The work done by the force →F in moving the particle from position A to position B along the circular path is:
W=F⋅R
---
The particle moves along a circular path from point A to point B. The radius of the circular path is R.
As the particle moves from A to B, it rises vertically to a height equal to the radius R. Therefore, the vertical displacement h is R.
The work done W by a force is given by the formula:
W=F⋅s⋅cos(θ)
where:
- F is the magnitude of the force,
- s is the displacement,
- θ is the angle between the force and the direction of displacement.
In this case, the force →F is applied horizontally, while the displacement in the vertical direction is R. Therefore, the angle θ between the force and the direction of displacement is 0∘ (since the force is horizontal and the displacement is vertical).
Since the angle θ=0∘, we have:
cos(0∘)=1
Thus, the work done can be simplified to:
W=F⋅R⋅1=F⋅R
The work done by the force →F in moving the particle from position A to position B along the circular path is:
W=F⋅R
Topper's Solved these Questions
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (CIRCULAR MOTION)
17 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (COLLISION AND CENTRE OF MASS )
12 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (FRICTION)
14 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
Similar Questions
If y−x=80∘ then find the values of x and y.

View SolutionAt point P, the value of dydx is :

View SolutionRefer the given figure and identify correct statement(s)

View SolutionFind contact force between 2 kg and 3 kg blocks :-

View SolutionIdentify A,B,C and D,E
View SolutionWhat is the distance OA for the square shown in figure :-

View SolutionThe equation of straight line shown in figure is :

View SolutionWhat is the reading of micrometer screw gauge shown in figure

View SolutionComparison of C3andC4 plants:-

View SolutionIn the given fig. If DE||BC Find EC.
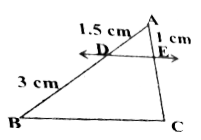
View Solution
