The position (x) of a particle of mass 2 kg moving along x-axis at time t is given by x=(2t3) metre. Find the work done by force acting on it in time interval t=0 to t=2 is :-
576 J
584 J
623 J
None
The correct Answer is:A
To solve the problem, we need to find the work done by the force acting on a particle of mass 2 kg, given its position as a function of time. The position is given by:
x(t)=2t3 meters
Step 1: Find the velocity of the particle.
The velocity v(t) is the derivative of the position x(t) with respect to time t:
v(t)=dxdt=ddt(2t3)=6t2 m/s
Step 2: Find the acceleration of the particle.
The acceleration a(t) is the derivative of the velocity v(t):
a(t)=dvdt=ddt(6t2)=12t m/s2
Step 3: Calculate the kinetic energy at t=0 and t=2.
The kinetic energy KE is given by the formula:
KE=12mv2
- At t=0:
v(0)=6(0)2=0 m/s
KE(0)=12×2×(0)2=0 J
- At t=2:
v(2)=6(2)2=6×4=24 m/s
KE(2)=12×2×(24)2=1×576=576 J
Step 4: Calculate the work done by the force.
According to the work-energy theorem, the work done W is equal to the change in kinetic energy:
W=KE(2)−KE(0)=576 J−0 J=576 J
Thus, the work done by the force acting on the particle in the time interval from t=0 to t=2 seconds is:
576 J
---
KE(0)=12×2×(0)2=0 J
KE(2)=12×2×(24)2=1×576=576 J
Topper's Solved these Questions
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (CIRCULAR MOTION)
17 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (COLLISION AND CENTRE OF MASS )
12 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (FRICTION)
14 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
Similar Questions
The position (x) of a particle of mass 1 kg moving along x-axis at time t is given by (x=12t2) metre. Find the work done by force acting on it in time interval from t=0 to t=3 s.
View SolutionThe position (x) of a particle of mass 1 kg moving along x-axis at time t is given by (x=12t2) meter. Find the work done by force acting on it in time interval from t=0 to t=3 s.
View SolutionA particle of mass 3 kg is moving along x - axis and its position at time t is given by equation x=(2t2+5)m. Work done by all the force acting on it in time interval t=0 to t=3s is
View SolutionThe displacement x of a particle moving along x-axis at time t is given by x2=2t2+6t. The velocity at any time t is
View SolutionThe position of a body moving along x-axis at time t is given by x=(t2−4t+6)m. The velocity of the body at time t = 3s is
View SolutionDisplacement of a particle of mass 2 kg varies with time as s=(2t2−2t+10)m. Find total work done on the particle in a time interval from t=0 to t=2s.
View SolutionThe position x of a particle moving along x - axis at time (t) is given by the equation t=√x+2, where x is in metres and t in seconds. Find the work done by the force in first four seconds
View SolutionThe position (X)-time (t) graph for a particle of mass 1 kg moving along x-axis is shown in figure. Find impulse on particle at t = 4 s.
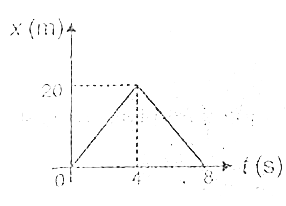
View SolutionThe position of a particle along X-axis at time t is given by x=2+t−3t2. The displacement and the distance travelled in the interval, t = 0 to t = 1 are respectively
View SolutionThe position of a particle moving along x-axis is given by x=10t−2t2. Then the time (t) at which it will momentily come to rest is
View Solution
