Two circular loops A and B of radii R and 2R respectively are made of the similar wire. Their moments of inertia about the axis passing through the centre of perpendicular to their plane are IA and IB respectively. The ratioIAIB is :
14
18
12
1
The correct Answer is:B
To find the ratio of the moments of inertia IAIB for two circular loops A and B with radii R and 2R respectively, we can follow these steps:
Step 1: Understand the Moment of Inertia for a Ring
The moment of inertia I of a ring about an axis perpendicular to its plane and passing through its center is given by the formula:
I=mr2
where m is the mass of the ring and r is its radius.
Step 2: Define the Masses of the Rings
Since both loops are made of similar wire, they have the same linear mass density. The mass of loop A (radius R) can be denoted as mA and the mass of loop B (radius 2R) as mB.
Using the relationship of mass and circumference:
- For loop A:
mA=σ⋅(2πR)
- For loop B:
mB=σ⋅(2π(2R))=σ⋅(4πR)
Step 3: Relate the Masses
Since both loops are made of similar wire, we can express the mass of loop B in terms of loop A:
mB=2⋅mA
Step 4: Calculate the Moments of Inertia
Now we can calculate the moments of inertia for both loops:
- For loop A:
IA=mAR2
- For loop B:
IB=mB(2R)2=mB⋅4R2
Step 5: Substitute the Mass of Loop B
Substituting mB=2mA into the equation for IB:
IB=(2mA)⋅4R2=8mAR2
Step 6: Find the Ratio of Moments of Inertia
Now we can find the ratio IAIB:
IAIB=mAR28mAR2
The mAR2 terms cancel out:
IAIB=18
Final Answer
Thus, the ratio IAIB is:
IAIB=14
The moment of inertia I of a ring about an axis perpendicular to its plane and passing through its center is given by the formula:
I=mr2
where m is the mass of the ring and r is its radius.
Since both loops are made of similar wire, they have the same linear mass density. The mass of loop A (radius R) can be denoted as mA and the mass of loop B (radius 2R) as mB.
- For loop A:
mA=σ⋅(2πR)
- For loop B:
mB=σ⋅(2π(2R))=σ⋅(4πR)
Since both loops are made of similar wire, we can express the mass of loop B in terms of loop A:
mB=2⋅mA
Now we can calculate the moments of inertia for both loops:
- For loop A:
IA=mAR2
- For loop B:
IB=mB(2R)2=mB⋅4R2
Substituting mB=2mA into the equation for IB:
IB=(2mA)⋅4R2=8mAR2
Now we can find the ratio IAIB:
IAIB=mAR28mAR2
The mAR2 terms cancel out:
IAIB=18
Thus, the ratio IAIB is:
IAIB=14
Topper's Solved these Questions
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (GRAVITATION)
25 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Properties of Matter & Fluid Mechanics)(Elasticity)
20 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (COLLISION AND CENTRE OF MASS )
12 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
Similar Questions
Moment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
View SolutionThe moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
View SolutionIf two circular discs A and B are of same mass but of radii r and 2r respectively, then the moment of inertia of A is
View SolutionThe ratio of radii of gyration of a circular ring and a circular disc, of the same mass and radius about an axis passing through their centres and perpendicular to their planes are
View SolutionTwo circular discs A and B of equal masses and thicknesses. But are made of metals with densities dAanddB(dA>dB). If their moments of inertia about an axis passing through the centre and normal to the circular faces be IAandIB, then.
View SolutionMoment of inertia of an ellipse shaped wire of mass 'm', semimajor axis 'a' about an axis passing through the centre and perpendicular to the plane of wire can be :
View SolutionThe moment of inertia of ring about an axis passing through its diameter is I. Then moment of inertia of that ring about an axis passing through its centre and perpendicular to its plane is
View SolutionTwo uniform circular loops A and B of radii r and nr are made of the same uniform wire. If moment of inertia of A about its axis is twice that of B, then find the value of n [diameter of wire is much smaller compared to radii of the loops].
View SolutionFind the moment of inertia of a circular disk or solid cylinder of radius R about the axis through the centre and perpendicular to the flat surface.
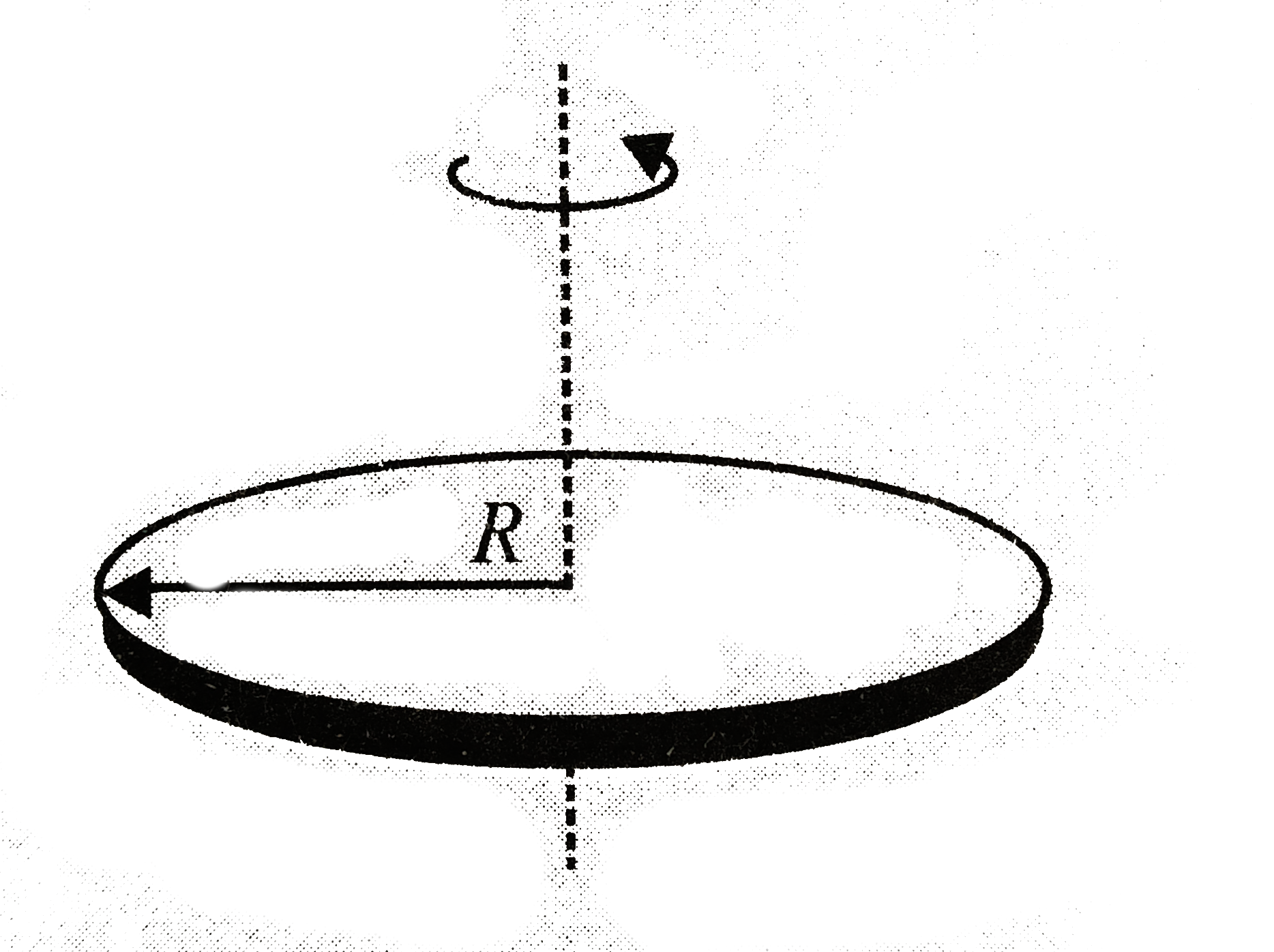
View SolutionFind the moment of inertia of a uniform rectangular plate of mass M and edges of length 'I' and 'b' about its axis passing through the centre and perpendicular to it.
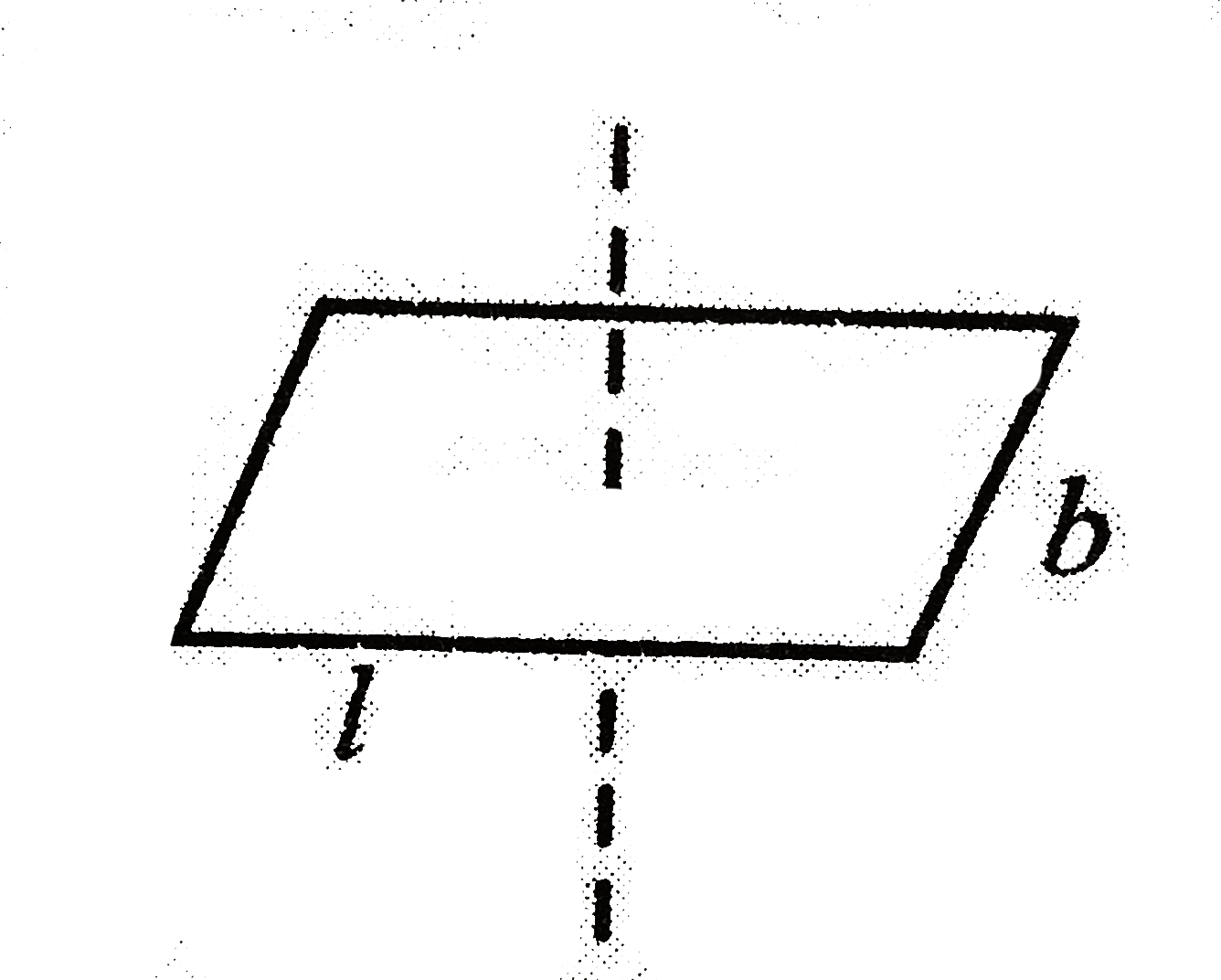
View Solution
