A particle is moving along a straight line parallel to x-axis with constant velocity. Find angular momentum about the origin in vector form
+mv2bˆk
−mvbˆk
−2mvbˆk
−mvbˆj
The correct Answer is:B
Step by step video & image solution for A particle is moving along a straight line parallel to x-axis with constant velocity. Find angular momentum about the origin in vector form by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (GRAVITATION)25videos
RACE
- BOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Properties of Matter & Fluid Mechanics)(Elasticity)20videos
RACE
- BOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (COLLISION AND CENTRE OF MASS )12videos
RACE
- BOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III28videos
NEWTONS LAWS OF MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example1videos
SIMPLE HARMONIC MOTION
Similar Questions
Knowledge Check
- Question 1 - Select One
A mass M moving with a constant velocity parallel to the X-axis. Its angular momentum with respect to the origin
Aa. is zeroBb. remains constantCc. goes on increasingDd. goes on decreasing
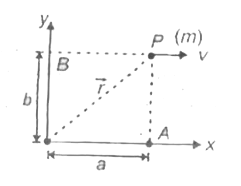
A particle of mass m is moving with constant velocity v parallel to the x-axis as shown in the figure. Its angular momentum about origin O is
 View Solution
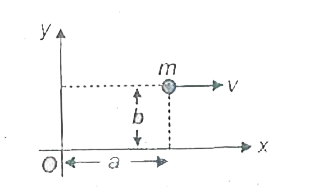
View SolutionA particle mass parallel to x-axis with constant velocity v as shown in the figure. The angular velocity of the particle about the origin O
View SolutionA particle moves on a straight line with a uniform velocity. It's angular momentum
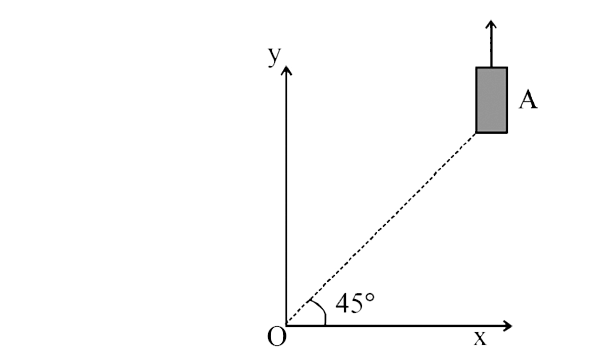
View SolutionOn a frictionless horizontal surface , assumed to be the x−y plane , a small trolley A is moving along a straight line parallel to the y-axis( see figure) with a constant velocity of (√3−1)m/s . At a particular instant , when the line OA makes an angle of 45(∘) with the x - axis , a ball is thrown along the surface from the origin O. Its velocity makes an angle ϕ with the x -axis and it hits the trolley .
(a) The motion of the ball is observed from the frame of the trolley . Calculate the angle θ made by the velocity vector of the ball with the x-axis in this frame .
(b) Find the speed of the ball with respect to the surface , if ϕ=(4θ)/(3).
 View Solution
View SolutionOn a frictionless horizontal surface , assumed to be the x−y plane , a small trolley A is moving along a straight line parallel to the y−axis ( see figure) with a constant velocity of (√3−1)m/s . At a particular instant , when the line OA makes an angle of 45(∘) with the x− axis , a ball is thrown along the surface from the origin O. Its velocity makes an angle ϕ with the x− axis and it hits the trolley .
(a) The motion of the ball is observed from the frame of the trolley . Calculate the angle θ made by the velocity vector of the ball with the x−axis in this frame .
(b) Find the speed of the ball with respect to the surface , if ϕ=(4θ)/(3).
 View Solution
View SolutionA particle is moving parallel to x-axis as shown in the figure. The angular velocity of the particle about the origin is
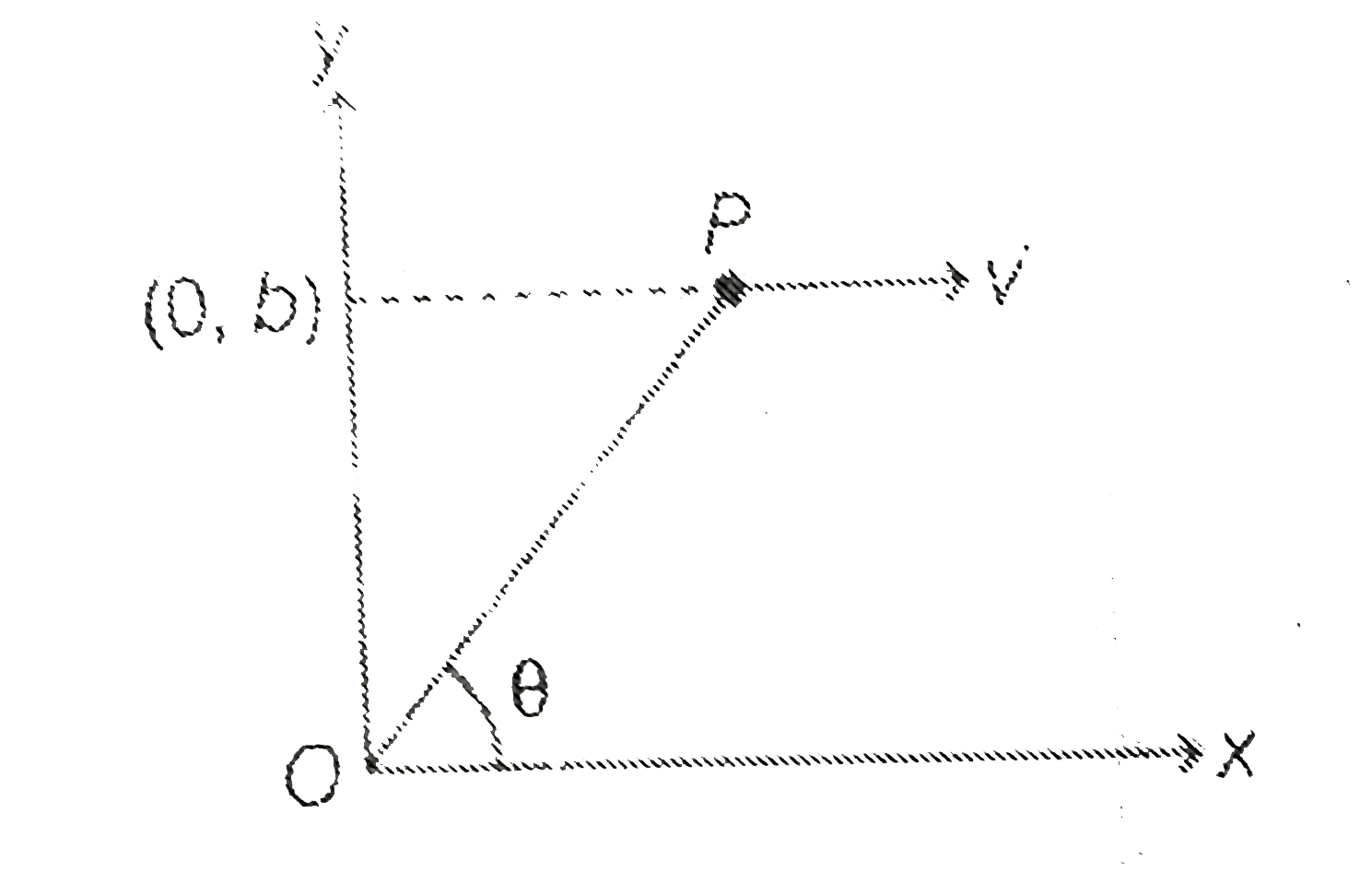 View Solution
View SolutionA particle of mass m=3kg moves along a straight line 4y−3x=2 where x and y are in metre, with constant velocity v=5ms−1 the magnitude of angular momentum about the origin is
View Solution

