An opaque cylindrical tank with an open top has a diameter of 3.00m and is completely filled with water .When the setting sun reaches an angle of 37∘ above the horizon,sunlight ceases to illuminate any part of the bottom of the tank .How deep is the tank?
3 m
4 m
5 m
Not possible
The correct Answer is:B
To solve the problem of finding the depth of the cylindrical tank, we will follow these steps:
Step 1: Understand the Geometry of the Situation
We have a cylindrical tank with a diameter of 3.00 m. The sunlight is coming at an angle of 37° above the horizon. We need to determine the depth of the tank (h) at which sunlight no longer reaches the bottom.
Step 2: Draw a Diagram
Draw a diagram of the cylindrical tank. Mark the diameter (3.00 m) and the angle of sunlight (37°). The sunlight will create a right triangle with the depth of the tank and the radius of the tank.
Step 3: Calculate the Angle of Incidence
The angle of incidence (i) can be calculated as:
i=90°−37°=53°
Step 4: Apply Snell's Law
Using Snell's Law, we have:
sin(i)sin(r)=n
where n is the refractive index of water (approximately 1.33).
Substituting the known values:
sin(53°)=0.79
Thus, we can write:
0.79sin(r)=1.33
Step 5: Solve for the Angle of Refraction
Rearranging gives:
sin(r)=0.791.33
Calculating this gives:
sin(r)≈0.60
Now, find the angle of refraction (r):
r=sin−1(0.60)≈36.87°
Step 6: Set Up the Right Triangle
In the right triangle formed by the radius (1.5 m, which is half of the diameter), the depth (h), and the angle of refraction (r):
tan(r)=oppositeadjacent=3 mh
Step 7: Calculate the Depth of the Tank
From the tangent function:
tan(36.87°)=3h
Calculating tan(36.87°) gives approximately 0.75. Therefore:
0.75=3h
Rearranging gives:
h=30.75=4 m
Conclusion
The depth of the tank is 4 meters.
---
We have a cylindrical tank with a diameter of 3.00 m. The sunlight is coming at an angle of 37° above the horizon. We need to determine the depth of the tank (h) at which sunlight no longer reaches the bottom.
Draw a diagram of the cylindrical tank. Mark the diameter (3.00 m) and the angle of sunlight (37°). The sunlight will create a right triangle with the depth of the tank and the radius of the tank.
The angle of incidence (i) can be calculated as:
i=90°−37°=53°
Using Snell's Law, we have:
sin(i)sin(r)=n
where n is the refractive index of water (approximately 1.33).
sin(53°)=0.79
Thus, we can write:
0.79sin(r)=1.33
Rearranging gives:
sin(r)=0.791.33
Calculating this gives:
sin(r)≈0.60
r=sin−1(0.60)≈36.87°
In the right triangle formed by the radius (1.5 m, which is half of the diameter), the depth (h), and the angle of refraction (r):
tan(r)=oppositeadjacent=3 mh
From the tangent function:
tan(36.87°)=3h
Calculating tan(36.87°) gives approximately 0.75. Therefore:
0.75=3h
h=30.75=4 m
The depth of the tank is 4 meters.
Topper's Solved these Questions
Similar Questions
A cylinderical tank of height 0.4 m is open at the top and has a diameter 0.16m. Water is filled in it up to height of 0.16 m. Find the time taken to empty the tank through a hole of radius 5×10−3m in its bottom.
View SolutionT=R2r2√2hg
Suppose an open cylindrical tank has a round drain with radius t in the bottom of the tank. When the tank is filled with water to a depth of h centimeters, the time it takes for all the water to drain from the tank is given by the formula above, where R is the radius of the tank (in centimeters) and g=980cm/s2 is the acceleration due to gravity. Suppose such a tank has a radius of 2 meters and is filled to a depth of 4 meters. About how many minutes does it take to empty the tank if the drain has a radius of 5 centimeters? (1 meter=100 centimeter).View SolutionA cylindrical water tank has a diameter of 14 meters and a height of 20 meters. A water truck can fill π cubic meters of the tank every minute. How long will take the water truck to fill water tank from empty to half full?
View SolutionA tank 5 m high is half filled with water and then is filled to top with oil of density 0.85g/cm3 The pressure at the bottom of the tank, due to these liquids is
View SolutionA cylindrical tank has a hole of 1cm2 in its bottom. If the water is allowed to flow into the tank from a tube above it at the rate of 70cm3/sec, then the maximum height up to which water can rise in the tank is
View SolutionA cylindrical tank has a hole of 1cm2 in its bottom. If the water is allowed to flow into the tank from a tube above it at the rate of 70cm3/sec, then the maximum height up to which water can rise in the tank is
View SolutionAn open rectangular tank 1.5 m wide 2m deep ad 2 m long is half filled with water. It is accelerated horizontally at 3.27m/s2 in the direction of its length determine the depth of water at each end of tank.
View Solution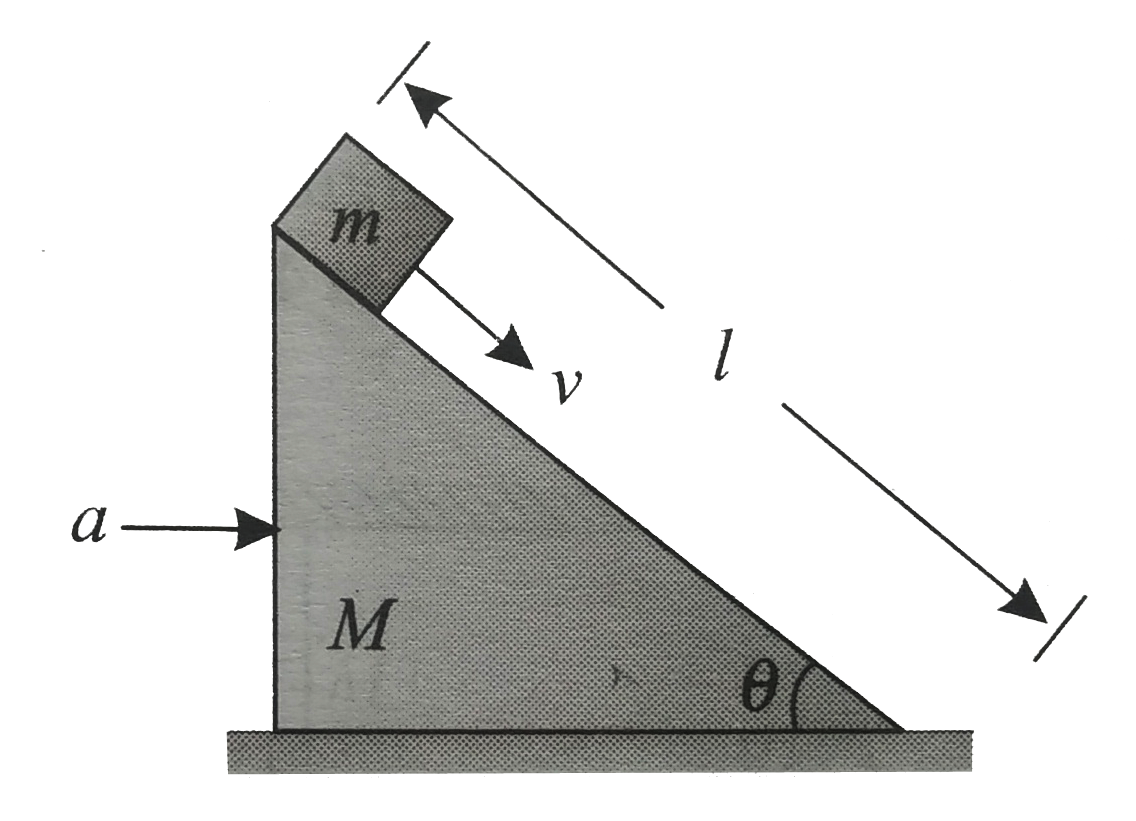
A smooth wedge of mass M is pushed with an acceleration a=>anθ and a block of mass m is projected down the slant with a velocity v relative to the wedge.
The horizontal force applied on the wedge is:View SolutionA cylindrical tank of height H is open at the top end and it has a radius r. Water is filled in it up to a height of h. The time taken to empty the tank through a hole of radius r' in its bottom is
View SolutionA cylindrical tank of height 2 m is open at the top and has a radius 50 cm. Water is filled in it upto a height 1.75 m. Calculate how long it will take to empty the tank through a hole of radius 0.05 cm in its bottom.
View Solution

