Calculate the resistance of two coils if their equivalent resistance in series and parallel are respectively 18Ω and 4Ω
12Ω,6Ω
15Ω,3Ω
8Ω,10Ω
16Ω,2Ω
To solve the problem of calculating the resistance of two coils given their equivalent resistance in series and parallel, we can follow these steps:
Step 1: Define the Variables
Let the resistances of the two coils be R and R1.
Step 2: Write the Equation for Series Resistance
The equivalent resistance in series is given by the formula:
Rseries=R+R1
According to the problem, this is equal to 18 ohms:
R+R1=18(1)
Step 3: Write the Equation for Parallel Resistance
The equivalent resistance in parallel is given by the formula:
Rparallel=R⋅R1R+R1
According to the problem, this is equal to 4 ohms:
R⋅R1R+R1=4(2)
Step 4: Substitute Equation (1) into Equation (2)
From Equation (1), we can express R1 in terms of R:
R1=18−R
Now substitute this into Equation (2):
R(18−R)18=4
Step 5: Simplify and Solve for R
Cross-multiplying gives us:
R(18−R)=4⋅18
R(18−R)=72
Expanding this, we get:
18R−R2=72
Rearranging gives us a quadratic equation:
R2−18R+72=0(3)
Step 6: Factor the Quadratic Equation
To factor the quadratic equation R2−18R+72=0, we look for two numbers that multiply to 72 and add to -18. The factors are -12 and -6:
(R−12)(R−6)=0
Step 7: Solve for R
Setting each factor to zero gives us:
R−12=0⇒R=12
R−6=0⇒R=6
Step 8: Find R1
Using Equation (1) to find R1:
1. If R=12:
R1=18−12=6
2. If R=6:
R1=18−6=12
Final Result
The resistances of the two coils are:
- R=12Ω and R1=6Ω
- or R=6Ω and R1=12Ω
Let the resistances of the two coils be R and R1.
The equivalent resistance in series is given by the formula:
Rseries=R+R1
According to the problem, this is equal to 18 ohms:
R+R1=18(1)
The equivalent resistance in parallel is given by the formula:
Rparallel=R⋅R1R+R1
According to the problem, this is equal to 4 ohms:
R⋅R1R+R1=4(2)
From Equation (1), we can express R1 in terms of R:
R1=18−R
Now substitute this into Equation (2):
R(18−R)18=4
Cross-multiplying gives us:
R(18−R)=4⋅18
R(18−R)=72
Expanding this, we get:
18R−R2=72
Rearranging gives us a quadratic equation:
R2−18R+72=0(3)
To factor the quadratic equation R2−18R+72=0, we look for two numbers that multiply to 72 and add to -18. The factors are -12 and -6:
(R−12)(R−6)=0
Setting each factor to zero gives us:
R−12=0⇒R=12
R−6=0⇒R=6
Using Equation (1) to find R1:
1. If R=12:
R1=18−12=6
2. If R=6:
R1=18−6=12
The resistances of the two coils are:
- R=12Ω and R1=6Ω
- or R=6Ω and R1=12Ω
Topper's Solved these Questions
Similar Questions
Knowledge Check
The total resistance in the parallel combination of three resistances 9Ω,7Ωand5Ω
A1.22ΩB2.29ΩC4.22ΩD2.02Ω
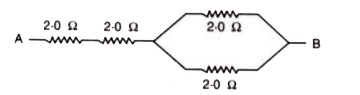
Calculate the equivalent resistance between the points A and B in Fig. if each resistance is 2.0Ω
View SolutionYou are given two resistance R1=(4.0±0.1)Ω and R2=(9.1±0.2)Ω. Calculate their effective resistance when they are connected (i) in series and (ii) in parallel. Also calculate the percentage error in each case.
View SolutionFor the series combination of three resistors establish the relation :
R=R1+R2+R3
where the symbols have their usual meanings.
Calculate the equivalent resistance of the combination of three resistors of 6Ω,9Ω and 18Ω joined in parallel.
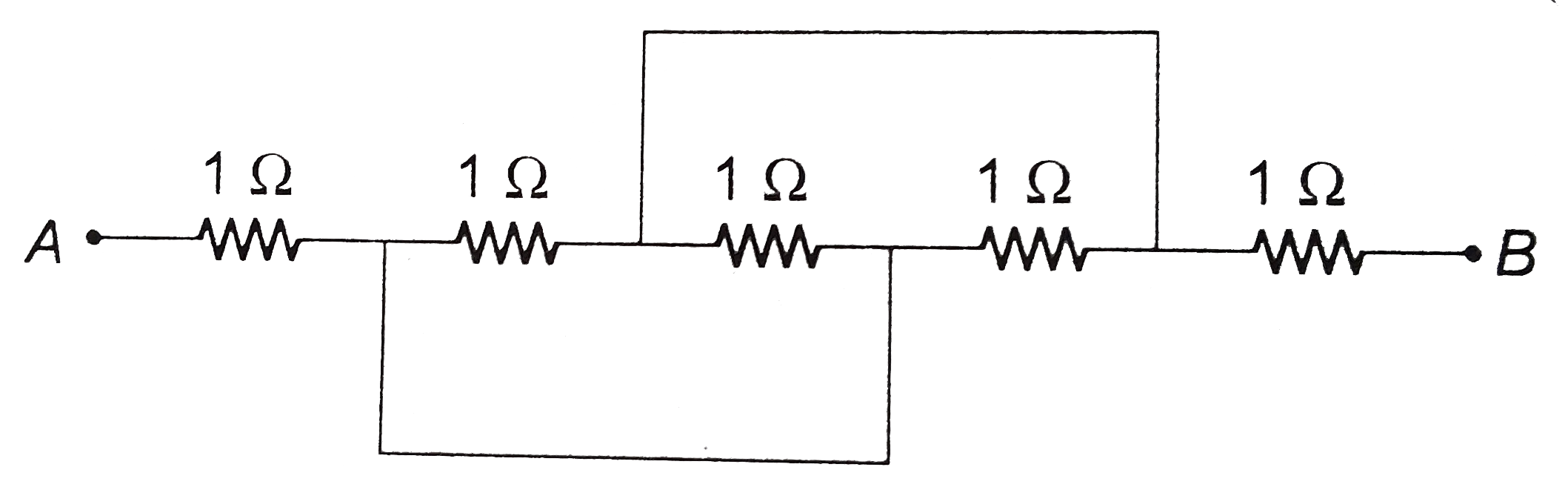
View SolutionEquivalent resistance between the points A and B (in Ω)
 .
.
View SolutionThe equivalent resistance of two resistor connected in series is 6Ω and their equivalent resistance is 43Ω. What are the values of resistances ?
View SolutionIn the circuit diagram given below, a cell of 9 V and internal resistance of 0.5(Ω) is connected across a resistor A of 2Ω in series and two resistors of 2Ω and 6Ω in parallel.
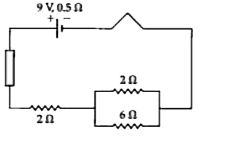
Find
The total resistance
View SolutionIn the circuit shown below in Fig., calculate the value of x if the equivalent resistance between the points A and B is 4 Ω

View Solution