An ideal gas is taken through a process PT3= constant. The coefficient of thermal expansion of the gas in the given process is
1/T
2/T
3/T
4/T
The correct Answer is:D
To solve the problem of finding the coefficient of thermal expansion of an ideal gas undergoing a process where PT3=constant, we can follow these steps:
1. Understand the Given Process:
We are given that PT3=constant. This implies that as pressure P and temperature T change, their product with T3 remains constant.
2. Use the Ideal Gas Law:
Recall the ideal gas law, which states:
PV=nRT
where n is the number of moles, R is the ideal gas constant, and V is the volume.
3. Express Pressure in Terms of Volume and Temperature:
From the ideal gas law, we can express pressure P as:
P=nRTV
Substituting this into the given process equation PT3=constant:
nRTVT3=constant
This simplifies to:
nRT4V=constant
4. Rearranging the Equation:
Rearranging gives us:
T4=constant⋅V
This indicates that T4 is proportional to V.
5. Differentiate the Relationship:
To find the coefficient of thermal expansion γ, we differentiate both sides with respect to temperature:
d(T4)dT=dVdT
Using the chain rule, we have:
4T3dTdT=dVdT⇒4T3=dVdT
6. Relate Changes in Volume and Temperature:
We can express the changes in volume and temperature as:
ΔVV=dVdTΔT
Therefore, we can write:
ΔVV=4T3ΔT
7. Define the Coefficient of Thermal Expansion:
The coefficient of thermal expansion γ is defined as:
γ=1VΔVΔT
Substituting our expression for ΔV:
γ=1V(4T3ΔT)1ΔT=4T3V
8. Final Expression:
Since V is not constant, we can express γ as:
γ=4T
Conclusion:
Thus, the coefficient of thermal expansion of the gas in the given process is:
γ=4T
We are given that PT3=constant. This implies that as pressure P and temperature T change, their product with T3 remains constant.
Recall the ideal gas law, which states:
PV=nRT
where n is the number of moles, R is the ideal gas constant, and V is the volume.
From the ideal gas law, we can express pressure P as:
P=nRTV
Substituting this into the given process equation PT3=constant:
nRTVT3=constant
This simplifies to:
nRT4V=constant
Rearranging gives us:
T4=constant⋅V
This indicates that T4 is proportional to V.
To find the coefficient of thermal expansion γ, we differentiate both sides with respect to temperature:
d(T4)dT=dVdT
Using the chain rule, we have:
4T3dTdT=dVdT⇒4T3=dVdT
We can express the changes in volume and temperature as:
ΔVV=dVdTΔT
Therefore, we can write:
ΔVV=4T3ΔT
The coefficient of thermal expansion γ is defined as:
γ=1VΔVΔT
Substituting our expression for ΔV:
γ=1V(4T3ΔT)1ΔT=4T3V
Since V is not constant, we can express γ as:
γ=4T
Thus, the coefficient of thermal expansion of the gas in the given process is:
γ=4T
Similar Questions
An ideal gas is expanding such that PT2=constant. The coefficient of volume expansion of the gas is-
View SolutionAn ideal gas is expanding such that PT2=constant. The coefficient of volume expansion of the gas is-
View Solutionan ideal gas is expanding such that PT=constant. The coefficient of the volume expansion of the gas is ( where symbols have their own meanings)
View SolutionIdeal gas is taken through the process shown in the figure :
View SolutionIdeal gas is taken through the process shown in the figure :

View SolutionAn ideal monatomic gas undergoes process PV1.25 = constant .Then
View SolutionA certain amount of ideal monoatomic gas undergoes a process given by TV1/2= constant. The molar specific heat of the gas for the process will be given by
View SolutionOne mole of an ideal monoatomic gas is taken through a polytropic process P2T = constant. The heat required to increase the temperature of the gas by ΔT is
View Solution
Two moles of an ideal monoatomic gas is taken through a cyclic process as shown in the P-T diagram. In the process BC, PT−2= constant. Then the ratio of heat absorbed and heat released by the gas during the process AB and process BC respectively is.
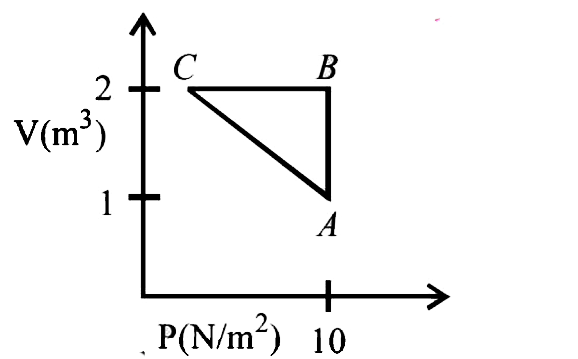
View SolutionAn ideal gas is taken through the cycle A→B→C→A, as shown in the figure, If the net heat supplied to the gas in the cycle is 5J, the work done by the gas in the process CtoA is
View Solution