Molecule of a gas in a container hits one wall (1) normally and rebounds back. It suffers number of collision and hits the opposite wall (2) which is at angle of 30∘ with wall 1. Assuming the collision to be elastic and the small collision time to be the same for both the walls. The magnitude of average force by walls and 2 are F1 and F2 provide to molecule during collision satisfy
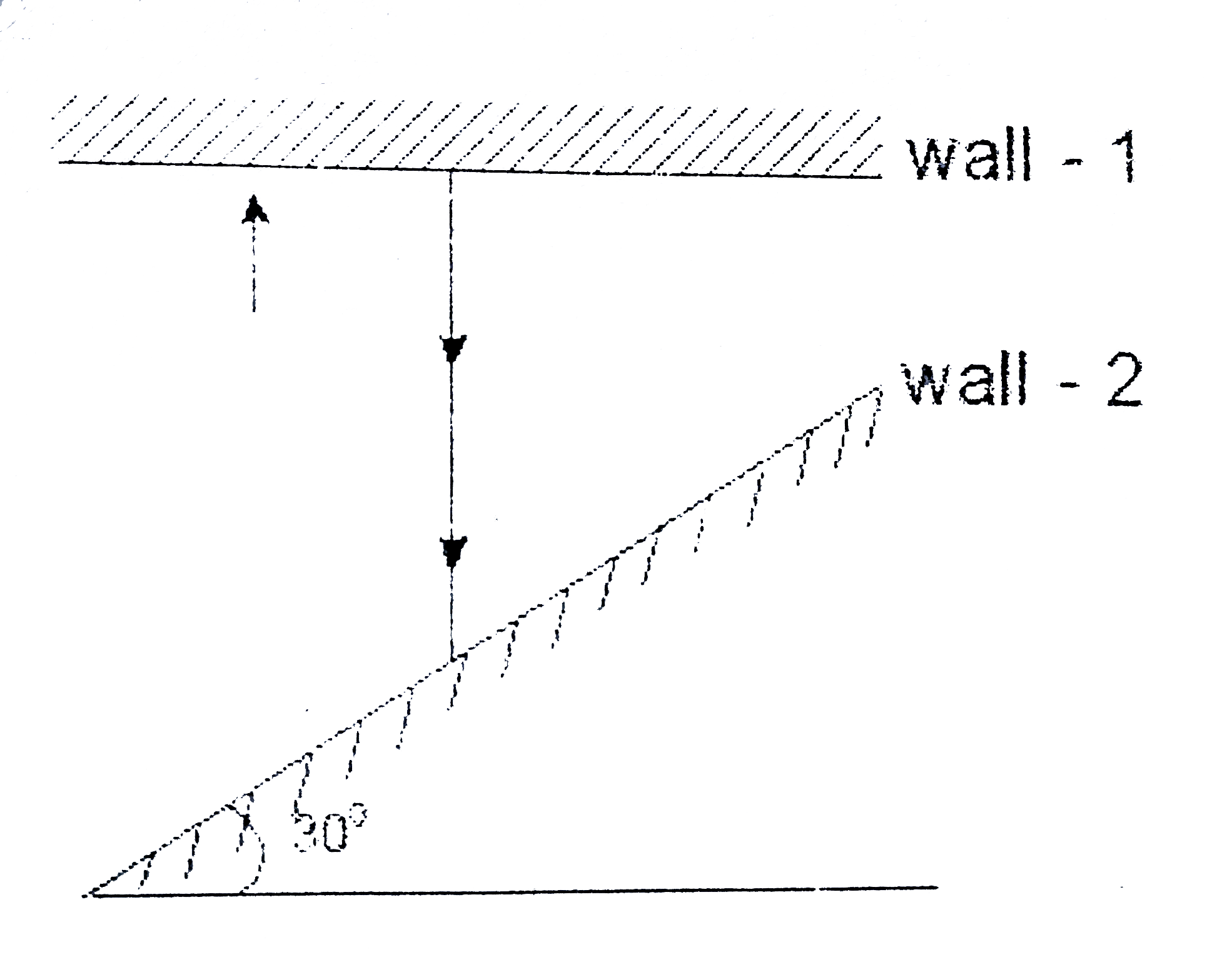
F1>F2
F1<F2
F1=F2 both non zero
F12F220
The correct Answer is:A
F1=2mvΔt F2=2mvcos30∘Δt
Hence F1>F2
Similar Questions
The collisions between the molecules and container exert ___________ on the walls of the container
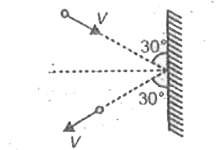
View SolutionA particle of mass m strikes a wall with speed v at an angle 30∘ with the wall elastically as shown in the figure. The magnitude of impulse imparted to the ball by the wall is
 View Solution
View SolutionA molecule of mass m moving at a velocity v impinges elastically on the wall at an angle α with the wall. Then
View SolutionA ping-pong ball strikes a wall with a velocity of 10ms−1. If the collision is perfectly elastic, find the velocity if ball after impact
View SolutionWhich one of the following has elastic wall ?
View SolutionA molecules in a gas container hits the wall with speed 200m/s at an angle 30∘ with the normal, and reboudns with the same speed. Is momentum conserved in the collision ? Is the collision elastic or inelastic ?
View SolutionCollisions between the molecules of a gas and its container exert pressure on the walls of the container. (T/F)
View SolutionIf a ball strickes with a velocity u1 at the wall which itself is approaching it with a velocity u2 then find the velocity of the ball after collision with the wall.
View SolutionA particle of mass m strikes elastically on a wall with velocity v, at an angle of 60∘ from the wall then magnitude of change in momentum of ball along the wall is
View SolutionIf gas molecules undergo, inelastic collision with the walls of the container
View Solution

