Magnetic field in the cylindrical regaion with its axis passing through O varies at a constant rate $\frac{d B}{d t}$ . A treangular imaginary loop ABC, with $A B = B C$ , is lying in this region as shown in the adjacent figure. The work done to move unit positive charge from A to B along the side AB is

$r^{2} \frac{d B}{d t}$

$π r^{2} \frac{d B}{d t}$

$\frac{r^{2}}{2} \frac{d B}{d t}$

$\frac{3 r^{2}}{4} \frac{d B}{d t}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

No e.m.f. will be induced in AC because electric lines of force are perpendicular to AC and e.m.f. induced in $A B =$ e.m.f. induced in BC.
$∴$ e.m.f. induced in $A B = \frac{1}{2} ∣ ∣ ∣ \frac{d ϕ}{d t} ∣ ∣ ∣ = \frac{1}{2} r^{2} \frac{d B}{d t}$

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Similar Questions

Magnetic field B in a cylindrical region of radius r varies according to the law $B = B_{0} t$ as shown in the figure. A fixed conducting loop ABCDA of resistance R is lying in the region as show . The current flowing through the loop is

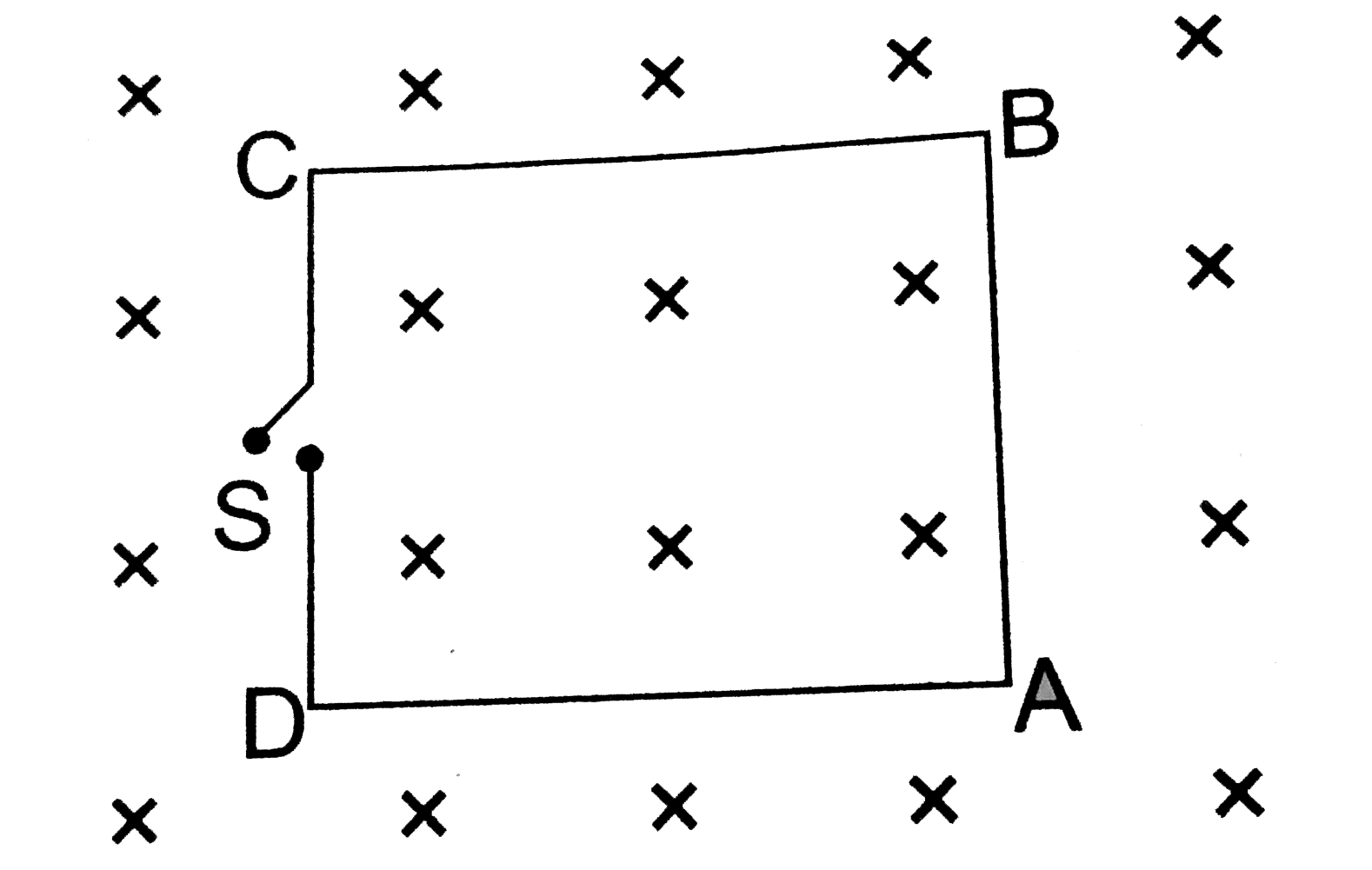
View Solution
The magnetic field in the cylindrical region shown in figure increase at a constant rate of $20 m T / sec$ . Each side of the square loop $A B C D$ has a length of $1 c m$ and resistance of $4 Ω$ . Find the current in the wire $A B$ if the switch $S$ is closed

View Solution
A charge q is uniformly distributed along the periphery of a non conducting uniform circular disc pivoted at its centre in a vertical plane and can freely rotate about a horizontal axis passing through its centre. A cylindrical region with its axis passing through the centre of the disc has a varying magnetic field B = kt as shown in the adjacent figure. wrapped over the disc as shown and remains stationary, then
View Solution
A uniform magnetic field is restricted within a region of radius r. The magnetic field changes with time at a rate $\frac{d B}{d t}$ . Loop 1 of radius R $>$ r encloses the region r and loop 2 of radius R is outside the region of magnetic field as shown in figure. Then, the emf generated is

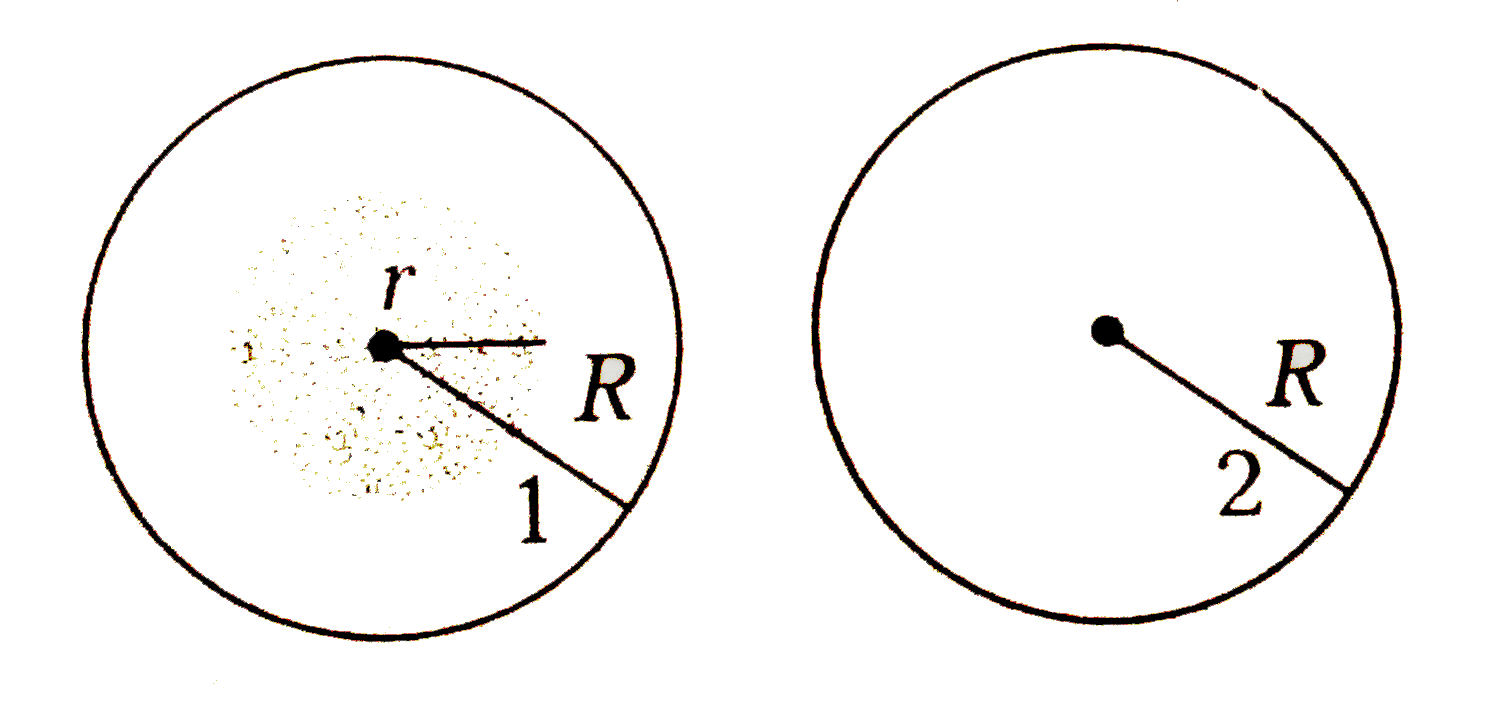
Zero in loop 1 and zero in loop 2
− d B d t π r 2 in loop 1 and − d B d t π 2 in loop 2
− d B d t π R 2 in loop 1 and zero in loop 2
− d B d t π r 2 in loop 1 and zero in loop 2
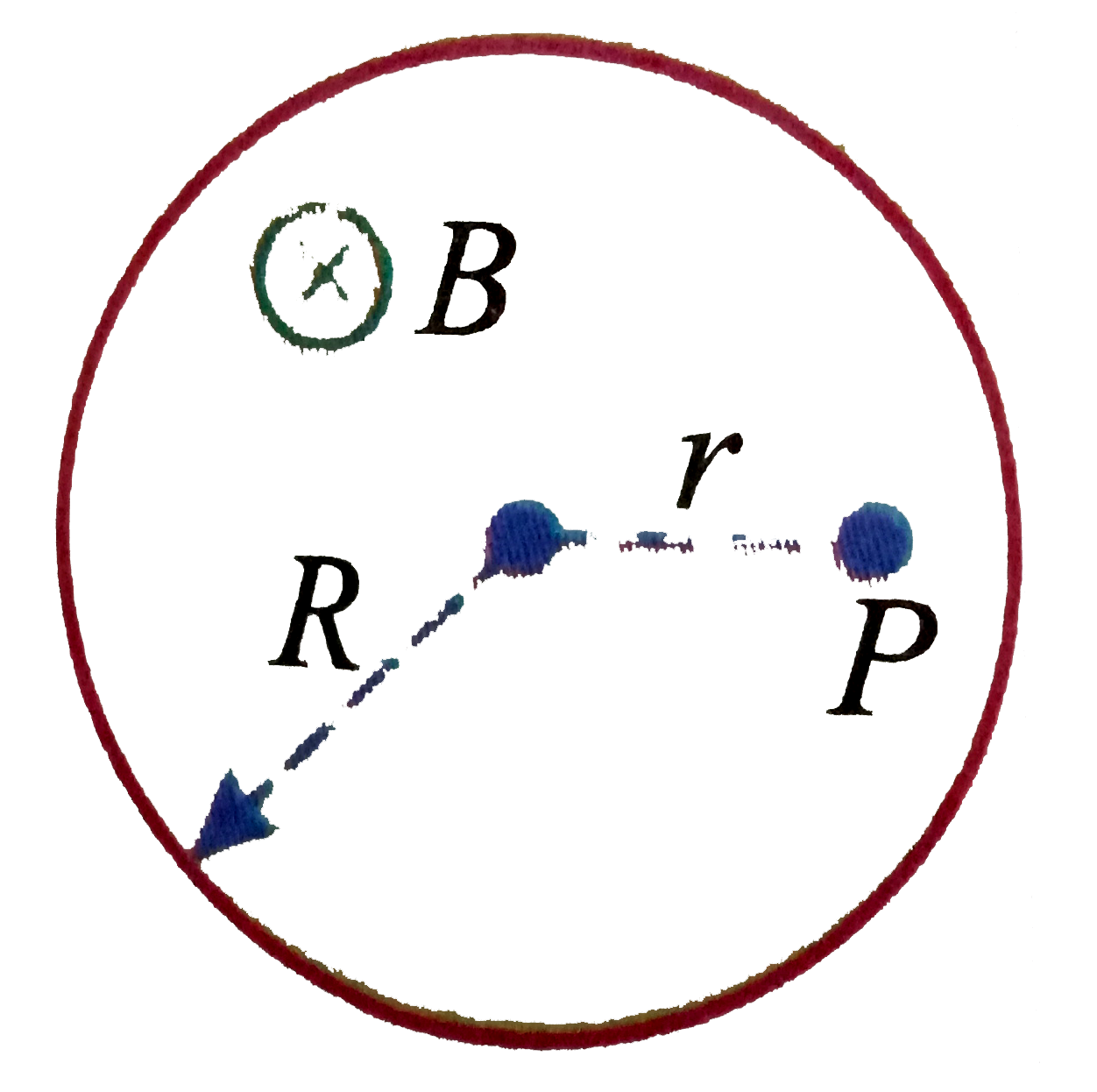
View Solution
A uniform magentic field of induction $B$ is confined in a cyclinderical region of radius $R$ . If the field is incresing at a constant rate of $\frac{d B}{d t} = α T / s$ , then the intensity of the electric field induced at point $P$ , distant $r$ from the axis as shown in the figure is proportional to :

View Solution
A uniform but time varying magnetic field exists in a cylindrical region as shown in the figure. The direction of magnetic field is into the plane of the paper and its magnitude is decreasing at a constant rate of $2 \times 10^{- 3} T / s$ . A particle of charge $1 μ C$ is moved slowly along circle of radius $1 m$ by an external force as shown in figure. The plane of the circle of radius $1 m$ by an external force as shown in figure. The plane of he circle lies in the plane of the paper and it is concentric with the cylindrical region. The work done by the external force in moving this charge along the circle will be

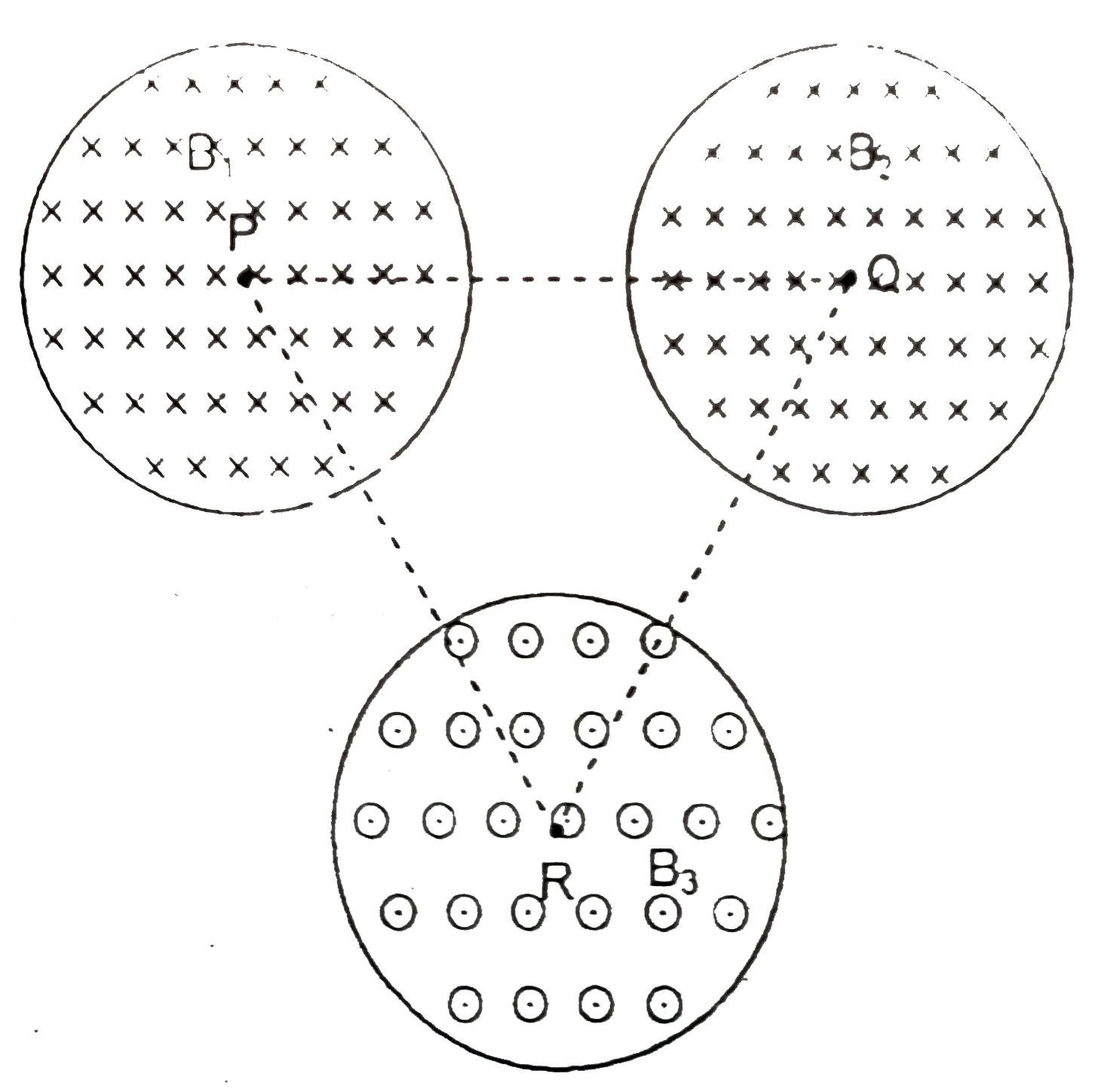
View Solution
In the figure $B_{1}$ , $B_{2}$ and $B_{3}$ represent uniform time varying magnetic fields in three different infinitely long cylindrical regions with axis passing through $P$ , $Q$ and $R$ and perpendicular to the plane of the paper. $P Q R$ is an equilateral triangle of side $4 \sqrt{3} r$ , where $r$ is radius of each cylindrical region $(r = 1 m)$ . The magnetic inductions vary with time $t$ as $B_{1} = A + a t$ , $B_{2} = A - b t$ and $B_{3} = A + c t$ . Here $a = 2 T e s l a / s$ , $b = 2 T e s l a / s$ and $c = 1 T e s l a / s$ and $A$ is a constant with dimensions of magnetic field and $' t'$ is time. Find the induced electric field strength at the centroid of the triangle $P Q R$ .

View Solution
A uniform magnetic field along a long cylindrical rod varies with time as $(B = α t)$ , where $α$ is positive constant. The electric field inside the rod as a function of radial distance r from the central axis is proportional to
View Solution
The arc AB with the centre C and the infinitely long wire having linear charge density $λ$ are lying in the same place. The minimum amount of work to be done to move a point charge $q_{0}$ from point A to B through a circuit path AB of radius a is equal to

View Solution
The are AB with the centre C and infinitely long wire having linear charge density $λ$ are lying in the same plane. The minium amount of work to be done to move a point charge $q_{0}$ from point A to B through a circular path AB of radius a is equal to

View Solution

Magnetic field in the cylindrical regaion with its axis passing through O varies at a constant rate dBdt. A treangular imaginary loop ABC, with AB=BC, is lying in this region as shown in the adjacent figure. The work done to move unit positive charge from A to B along the side AB is

The correct Answer is:C

No e.m.f. will be induced in AC because electric lines of force are perpendicular to AC and e.m.f. induced in AB= e.m.f. induced in BC. ∴ e.m.f. induced in AB=12∣∣∣dϕdt∣∣∣=12r2dBdt

Similar Questions

Recommended Questions

No e.m.f. will be induced in AC because electric lines of force are perpendicular to AC and e.m.f. induced in $A B =$ e.m.f. induced in BC.
$∴$ e.m.f. induced in $A B = \frac{1}{2} ∣ ∣ ∣ \frac{d ϕ}{d t} ∣ ∣ ∣ = \frac{1}{2} r^{2} \frac{d B}{d t}$