A uniform magnetic field along a long cylindrical rod varies with time as (B=αt), where α is positive constant. The electric field inside the rod as a function of radial distance r from the central axis is proportional to
A. r2
B. 1/r
C. 1r2
D. None of these
Step by step video & image solution for A uniform magnetic field along a long cylindrical rod varies with time as (B = alpha t), where alpha is positive constant. The electric field inside the rod as a function of radial distance r from the central axis is proportional to by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The displacement x of a particle varies with time t as x=ae−αt+beβt. Where a,b,α and β positive constant.
The velocity of the particle will.
View SolutionThe displacement x of a particle varies with time t as x=ae−αt+beβt. Where a,b,α and β positive constant.
The velocity of the particle will.
View Solution
Knowledge Check
A system consits of a uniformly charged sphere of radius R and a surrounding medium filled by a charge with the volume density ρ=αr, where α is a positive constant and r is the distance from the centre of the sphere. Find the charge of the sphere for which the electric field intensity E outside the sphere is independent of R.
Aα2ε0B2αε0C2παR2DNone of these
The magnitude of radius vector of a point varies with time as r=βt(1−αt) where α and β are positive constant. The distance travelled by this body over a closed path must be
View SolutionA time varying magnetic field B=Kr3t is existing in a cylindrical region of radius 'R' as shown (where k is a constant). The induced electric field 'E' at rR2 is
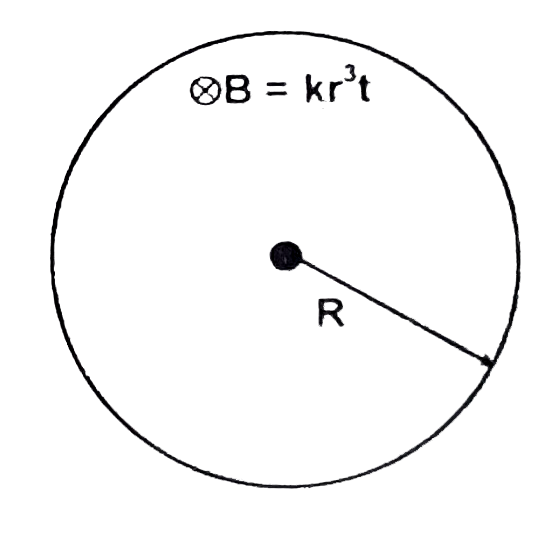
View SolutionA uniform but time varying magnetic field B=(2t3+24t)T is present in a cylindrical region of radius R=2.5cm as shown in figure.

The variation of electric field at any instant as a function of distance measured from the centre of cylinder in first problem is
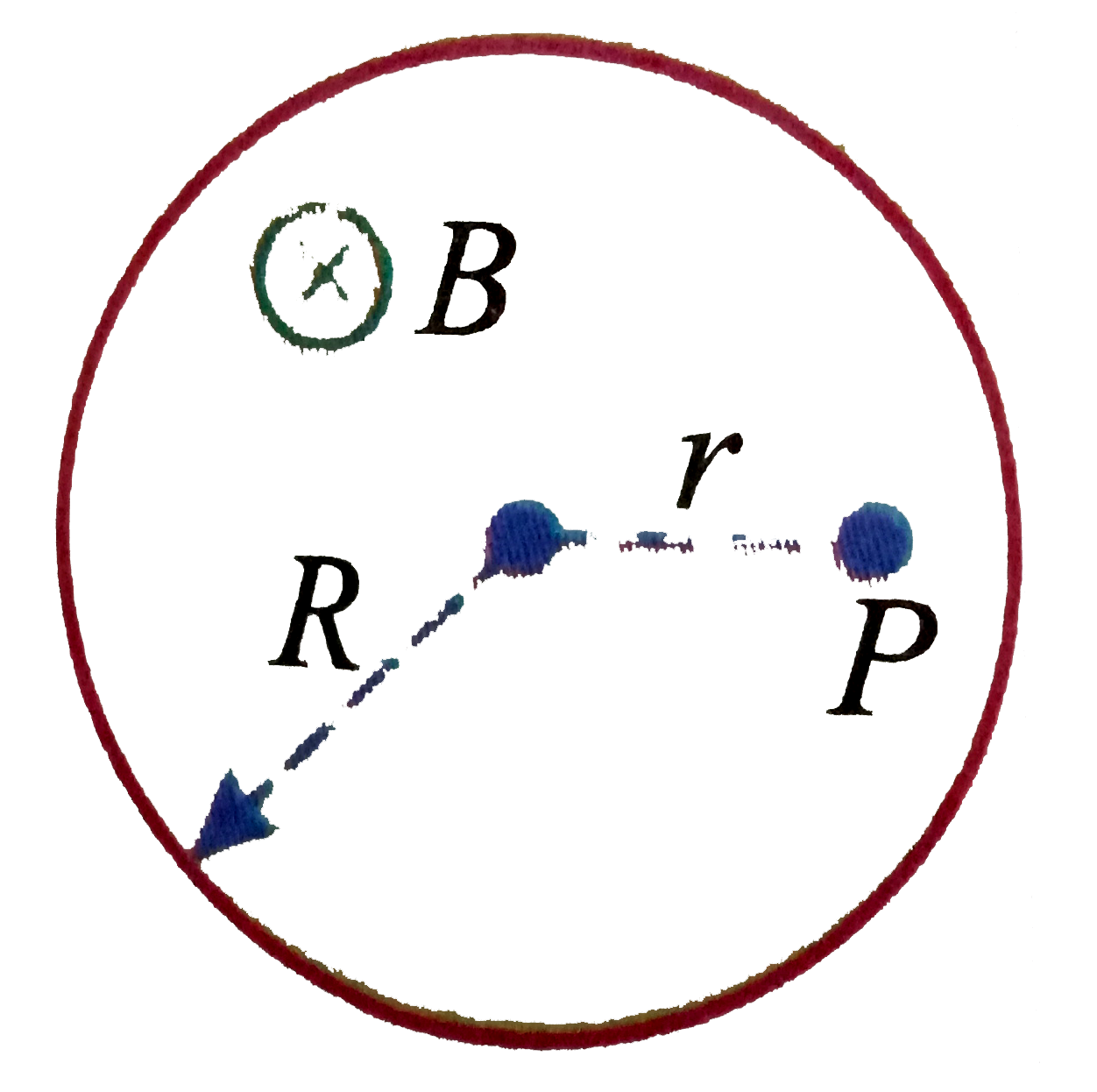
View SolutionA uniform magentic field of induction B is confined in a cyclinderical region of radius R. If the field is incresing at a constant rate of dBdt=αT/s, then the intensity of the electric field induced at point P, distant r from the axis as shown in the figure is proportional to :
View SolutionA time varying uniform magnetic field passes through a circular region of radius R. The magnetic field is directed outwards and it is a function of radial distance 'r' and time 't' according to relation B-B_(0)rt. The induced electric field strength at a radial distance R/2 from the centre will be.
View SolutionAn infinitely long hollow conducting cylinder with inner radius R2 and outer radius R carries a uniform current density along its length . The magnitude of the magnetic field , ∣∣→B∣∣ as a function of the radial distance r from the axis is best represented by
View SolutionThe electric field is a region (relative permittivity = 1) varies with distance "r" from origin according to relation E=Ar2ˆr, where A is a positive constant. The volume charge density in the region is proportional to
View Solution
