Find the acceleration of the two blocks shown in figure-2.101.Take g=10m/s2
The correct Answer is:A, C, D
To find the acceleration of the two blocks, we will follow these steps:
Step 1: Identify the forces acting on the blocks
- We have two blocks: Block A (2 kg) and Block B (3 kg).
- A force of 5 N acts on Block A (to the right).
- A force of 10 N acts on Block B (to the right).
- The coefficient of friction between the blocks and the surface is given as 0.1.
Step 2: Calculate the total external force
The total external force acting on the system of blocks is the sum of the forces acting on both blocks:
Fexternal=FA+FB=5N+10N=15N
Step 3: Calculate the frictional force
The frictional force between the blocks and the surface must be calculated to determine the net force acting on the system. The normal force (N) acting on the blocks is the weight of both blocks combined:
N=(mA+mB)⋅g=(2kg+3kg)⋅10m/s2=5kg⋅10m/s2=50N
The maximum static frictional force (F_friction) can be calculated as:
Ffriction=μ⋅N=0.1⋅50N=5N
Step 4: Calculate the net force
The net force (F_net) acting on the system is given by the total external force minus the frictional force:
Fnet=Fexternal−Ffriction=15N−5N=10N
Step 5: Calculate the total mass of the system
The total mass (m_total) of the system is the sum of the masses of both blocks:
mtotal=mA+mB=2kg+3kg=5kg
Step 6: Calculate the acceleration
Using Newton's second law, we can find the acceleration (a) of the system:
Fnet=mtotal⋅a⟹a=Fnetmtotal=10N5kg=2m/s2
Conclusion
The acceleration of the two blocks is:
2m/s2
- We have two blocks: Block A (2 kg) and Block B (3 kg).
- A force of 5 N acts on Block A (to the right).
- A force of 10 N acts on Block B (to the right).
- The coefficient of friction between the blocks and the surface is given as 0.1.
The total external force acting on the system of blocks is the sum of the forces acting on both blocks:
Fexternal=FA+FB=5N+10N=15N
The frictional force between the blocks and the surface must be calculated to determine the net force acting on the system. The normal force (N) acting on the blocks is the weight of both blocks combined:
N=(mA+mB)⋅g=(2kg+3kg)⋅10m/s2=5kg⋅10m/s2=50N
The maximum static frictional force (F_friction) can be calculated as:
Ffriction=μ⋅N=0.1⋅50N=5N
The net force (F_net) acting on the system is given by the total external force minus the frictional force:
Fnet=Fexternal−Ffriction=15N−5N=10N
The total mass (m_total) of the system is the sum of the masses of both blocks:
mtotal=mA+mB=2kg+3kg=5kg
Using Newton's second law, we can find the acceleration (a) of the system:
Fnet=mtotal⋅a⟹a=Fnetmtotal=10N5kg=2m/s2
The acceleration of the two blocks is:
2m/s2
Similar Questions
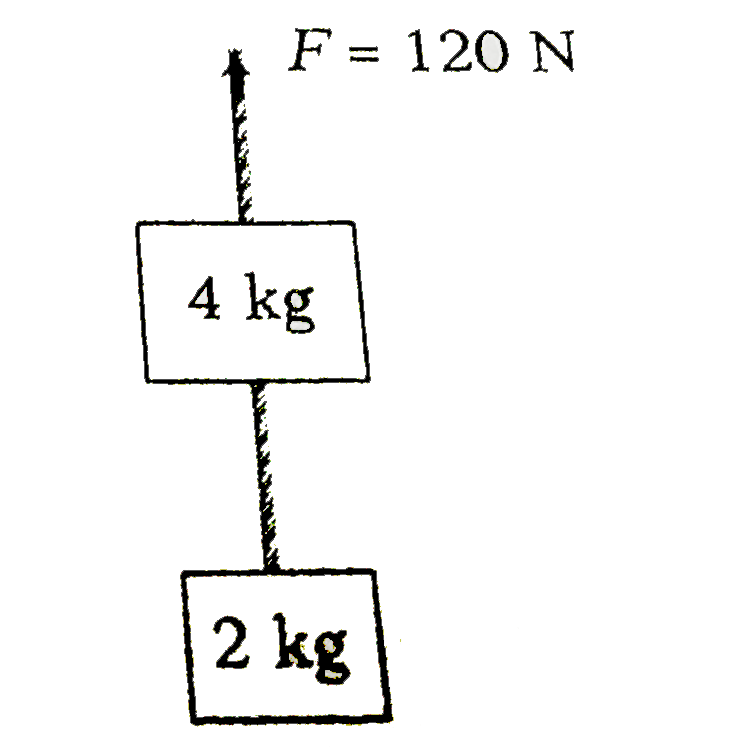
Two block of mass 4 kg and 2 kg are attached by an inextensible light string as shown in figure. Both the blocks are pulled vertically upwards by a force F=120N
Find
(a) the acceleration of the blocks
(b) tension in the string. (Take g=10ms−2)
View SolutionTwo block of mass 4 kg and 2 kg are attached by an inextensible light string as shown in figure. Both the blocks are pulled vertically upwards by a force F=120N

Find
(a) the acceleration of the blocks,
(b) tension in the string. (Take g=10ms−2)
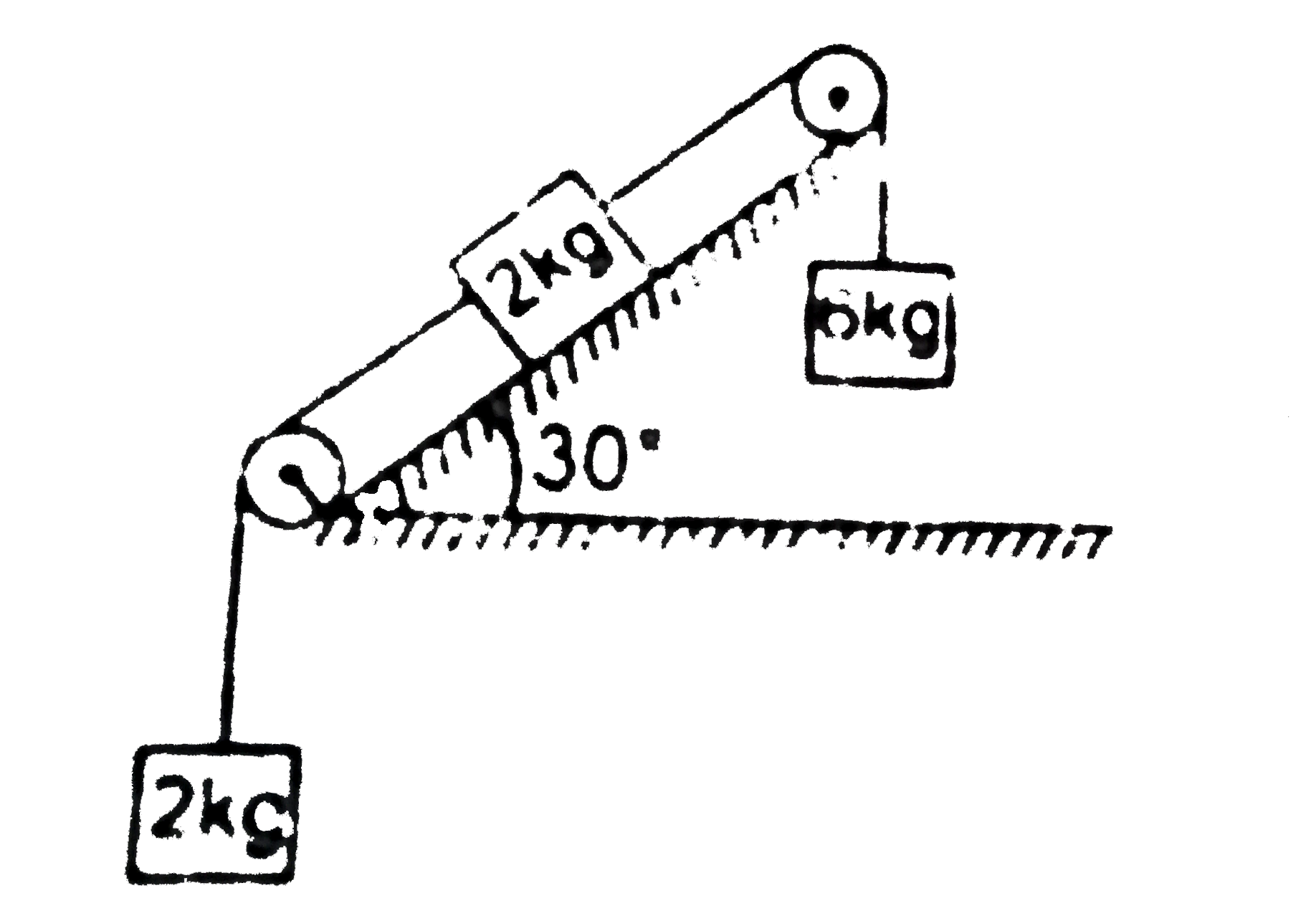
View SolutionFind the acceleration of the 6 kg block in the figure. All the surfaces and pulleys are smooth. Also the strings are inextensible and light. [Take g=10m/s2]
 .
.
View SolutionA 2 kg block is connected with two springs of force constants k1=100N/m and k2=300N/m as shown in figure. The block is released from rest with the springs unstretched. The acceleration of the block in its lowest postion is (g=10m/s2)

View SolutionFind the acceleration of the two blocks . The system is initialy at rest and the friction are as shown in fig .Given mA=mB=10kg
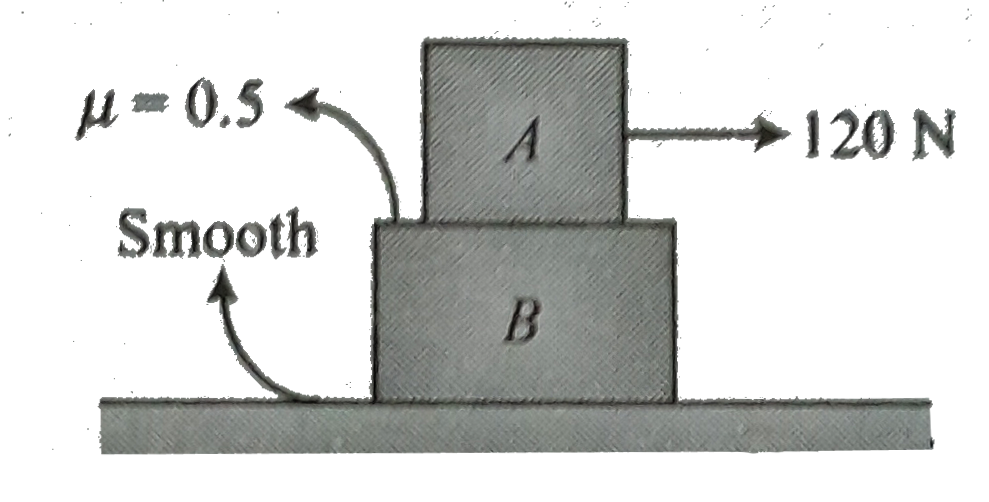
View SolutionThe friction coefficient between the horizontal surfce and ech of the blocks shown in figure is 0.20. The collision between the blocks is perfectly elastic. Find the separation between the two blocks when they come to rest. Take g=10ms2.
View SolutionIn figure shown if 2 kg block is moving at an acceleration 2m/s2, find the elongationin spring and acceleration of 4 kg block at this instant. Take g= 10m/s2.
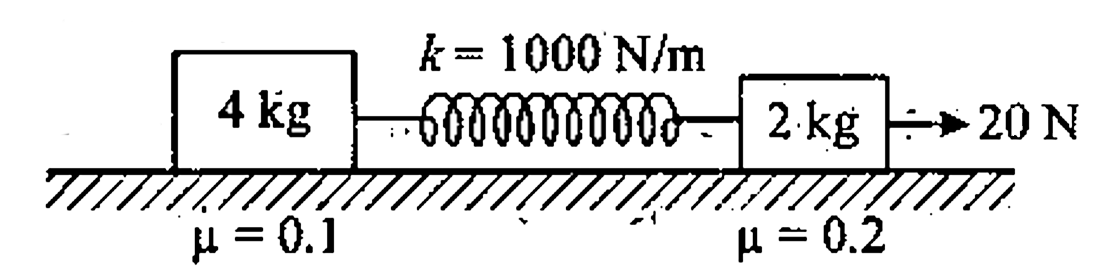
View SolutionIn the system shown in figure all surfaces are smooth. Strings is massless and inextensible.Find acceleration of the system and tension T in the string (g=10m/s2)
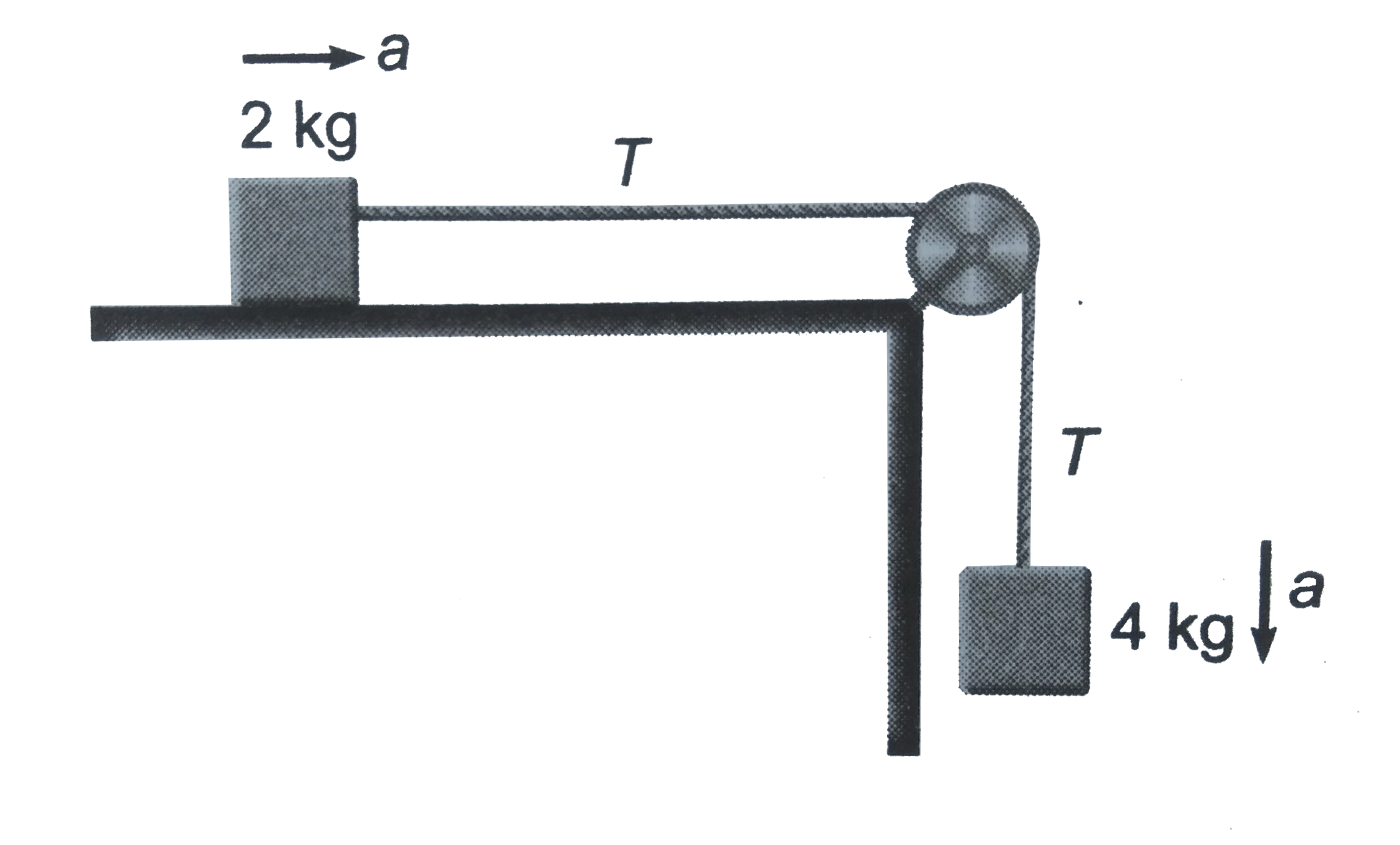
View Solution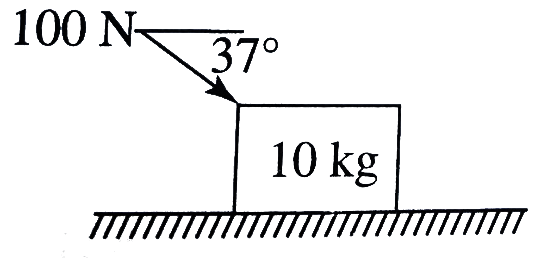
In the figure shoen calculate the angle of friction . The block dows not slide. Take g=10ms2.
View Solution
In the figure shoen calculate the angle of friction . The block dows not slide. Take g=10ms2.
View Solution