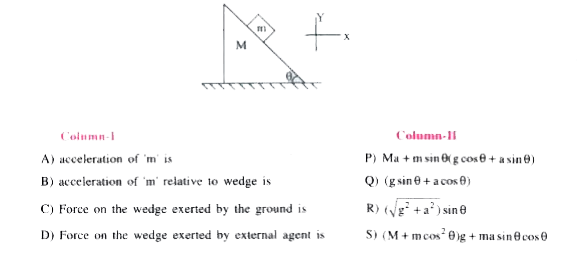
In the following figure all surfaces are smooth. The system is released from rest , then
A. acceleration of wedge greater then gtanθ
B. acceleration of m is
g√(1+2cos2θ)
C. acceleration of m is g
D. acceleration of wedge is gsinθ
acceleration of wedge greater then gtanθ
acceleration of m is g√(1+2cos2θ)
acceleration of m is g
acceleration of wedge is gsinθ
The correct Answer is:A, C, D
To solve the problem, we need to analyze the forces acting on the block and the wedge when the system is released from rest. Let's break it down step by step:
Step 1: Identify the Forces Acting on the Block
- The block (mass m) is on an inclined plane with angle θ.
- The gravitational force acting on the block is mg (downward).
- The component of this force acting parallel to the incline is mgsinθ.
- The component of the gravitational force acting perpendicular to the incline is mgcosθ.
Step 2: Analyze the Motion of the Block
- Since the surfaces are smooth, there is no friction.
- The net force acting on the block along the incline is mgsinθ.
- According to Newton's second law, the acceleration a of the block can be expressed as:
ma=mgsinθ
Therefore, the acceleration of the block a is:
a=gsinθ
Step 3: Identify the Forces Acting on the Wedge
- The wedge (mass M) experiences a normal force N from the block.
- This normal force can be resolved into two components: one acting perpendicular to the incline and the other acting parallel to the incline.
- The component of the normal force acting parallel to the incline is Nsinθ, which causes the wedge to accelerate horizontally.
Step 4: Apply Newton's Second Law to the Wedge
- The net force acting on the wedge in the horizontal direction is equal to the horizontal component of the normal force:
F=Nsinθ
- The acceleration A of the wedge can be expressed as:
MA=Nsinθ
Step 5: Relate the Normal Force to the Block's Acceleration
- From the block's perspective, the normal force N can be related to the acceleration of the block and the wedge.
- Since the block is accelerating down the incline with gsinθ, we can express N in terms of the accelerations:
N=m(gsinθ−A)
Step 6: Solve for the Accelerations
- Substitute N back into the equation for the wedge:
MA=m(gsinθ−A)sinθ
- Rearranging gives:
MA+mAsinθ=mgsin2θ
- Factor out A:
A(M+msinθ)=mgsin2θ
- Thus, the acceleration of the wedge A is:
A=mgsin2θM+msinθ
Conclusion
After analyzing the forces and applying Newton's laws, we conclude that:
- The acceleration of the block m is gsinθ.
- The acceleration of the wedge M is dependent on the mass ratio and angle.
Final Answers
- The correct options are:
- C: acceleration of m is gsinθ
- D: acceleration of the wedge is gsinθ
- The block (mass m) is on an inclined plane with angle θ.
- The gravitational force acting on the block is mg (downward).
- The component of this force acting parallel to the incline is mgsinθ.
- The component of the gravitational force acting perpendicular to the incline is mgcosθ.
- Since the surfaces are smooth, there is no friction.
- The net force acting on the block along the incline is mgsinθ.
- According to Newton's second law, the acceleration a of the block can be expressed as:
ma=mgsinθ
Therefore, the acceleration of the block a is:
a=gsinθ
- The wedge (mass M) experiences a normal force N from the block.
- This normal force can be resolved into two components: one acting perpendicular to the incline and the other acting parallel to the incline.
- The component of the normal force acting parallel to the incline is Nsinθ, which causes the wedge to accelerate horizontally.
- The net force acting on the wedge in the horizontal direction is equal to the horizontal component of the normal force:
F=Nsinθ
- The acceleration A of the wedge can be expressed as:
MA=Nsinθ
- From the block's perspective, the normal force N can be related to the acceleration of the block and the wedge.
- Since the block is accelerating down the incline with gsinθ, we can express N in terms of the accelerations:
N=m(gsinθ−A)
- Substitute N back into the equation for the wedge:
MA=m(gsinθ−A)sinθ
- Rearranging gives:
MA+mAsinθ=mgsin2θ
- Factor out A:
A(M+msinθ)=mgsin2θ
- Thus, the acceleration of the wedge A is:
A=mgsin2θM+msinθ
After analyzing the forces and applying Newton's laws, we conclude that:
- The acceleration of the block m is gsinθ.
- The acceleration of the wedge M is dependent on the mass ratio and angle.
- The correct options are:
- C: acceleration of m is gsinθ
- D: acceleration of the wedge is gsinθ
Similar Questions
All surfaces shown in figure are smooth. System is released from rest. x and y comonents of acceleration of COM are

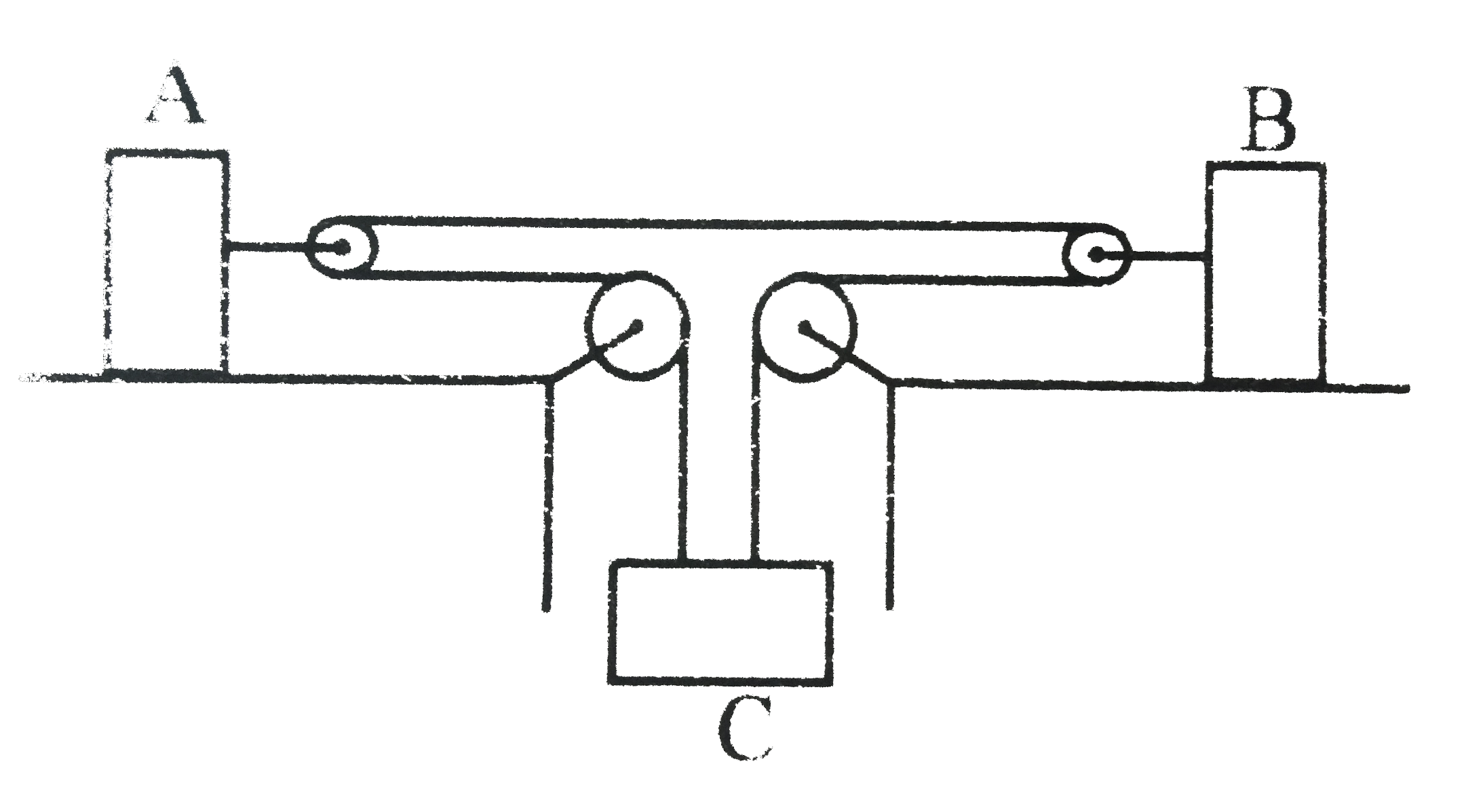
View SolutionIf acceleration of A is 2m/s2 to left and acceleration of B is 1m/s2 to left, then acceleration of C is-
View SolutionAll the surfaces are smooth as shown in figure. The acceleration of mass m relative to wedge is :

View SolutionIn a given figure the acceleration of M is (g=10ms−2)

View SolutionA stone is released from an elevator going up with an acceleration of g2. What is the acceleration of the stone just after release ?
View SolutionAll surface are smooth. Find the acceleration of mass m relative to wedge when wedge is moving with acceleration 'a'

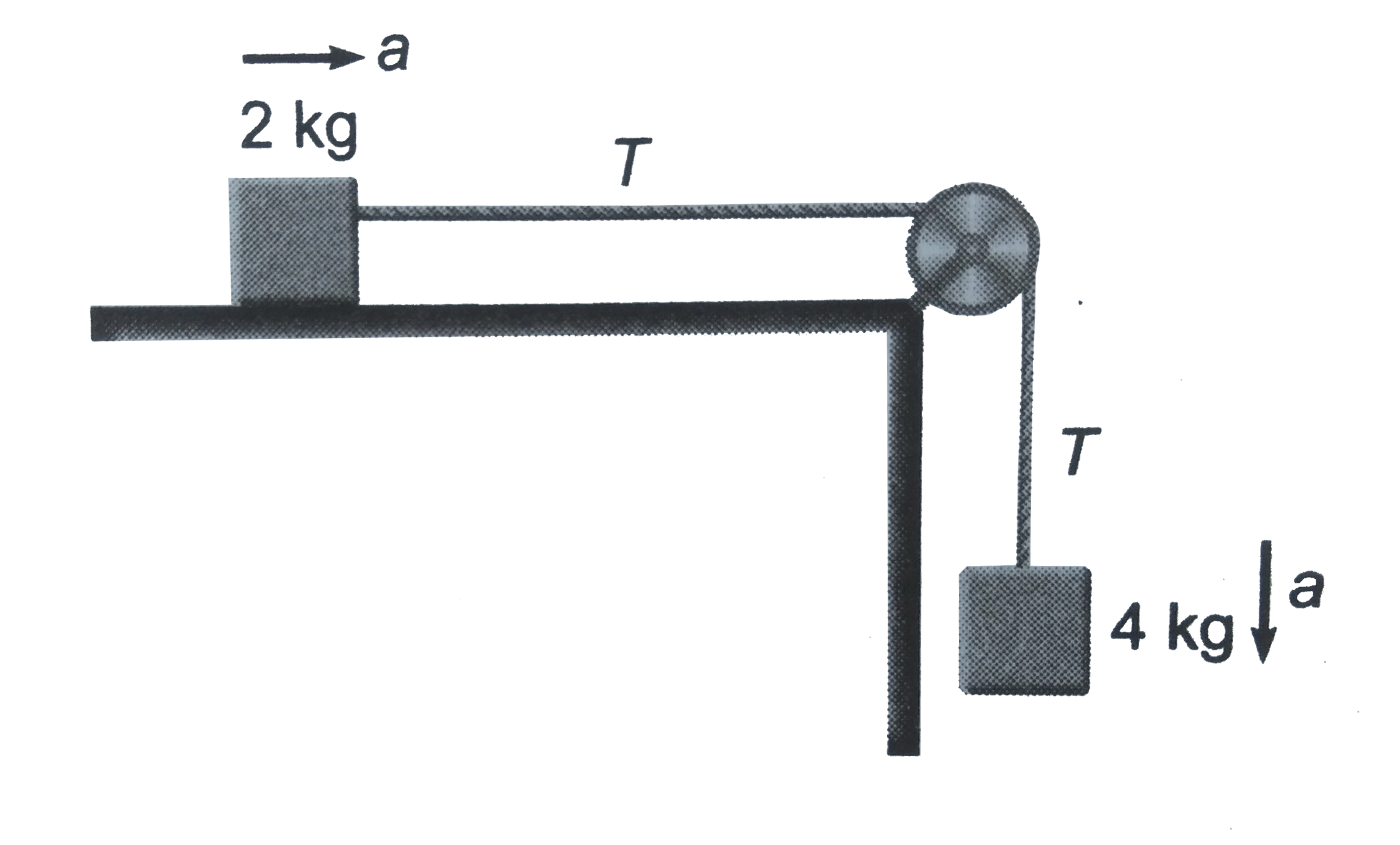
View SolutionIn the system shown in figure all surfaces are smooth. Strings is massless and inextensible.Find acceleration of the system and tension T in the string (g=10m/s2)
View SolutionThe system is released from rest. All surface are smooth . Find the angle theta at which the acceleration of wedge is maximum. ( given .Mm=12)
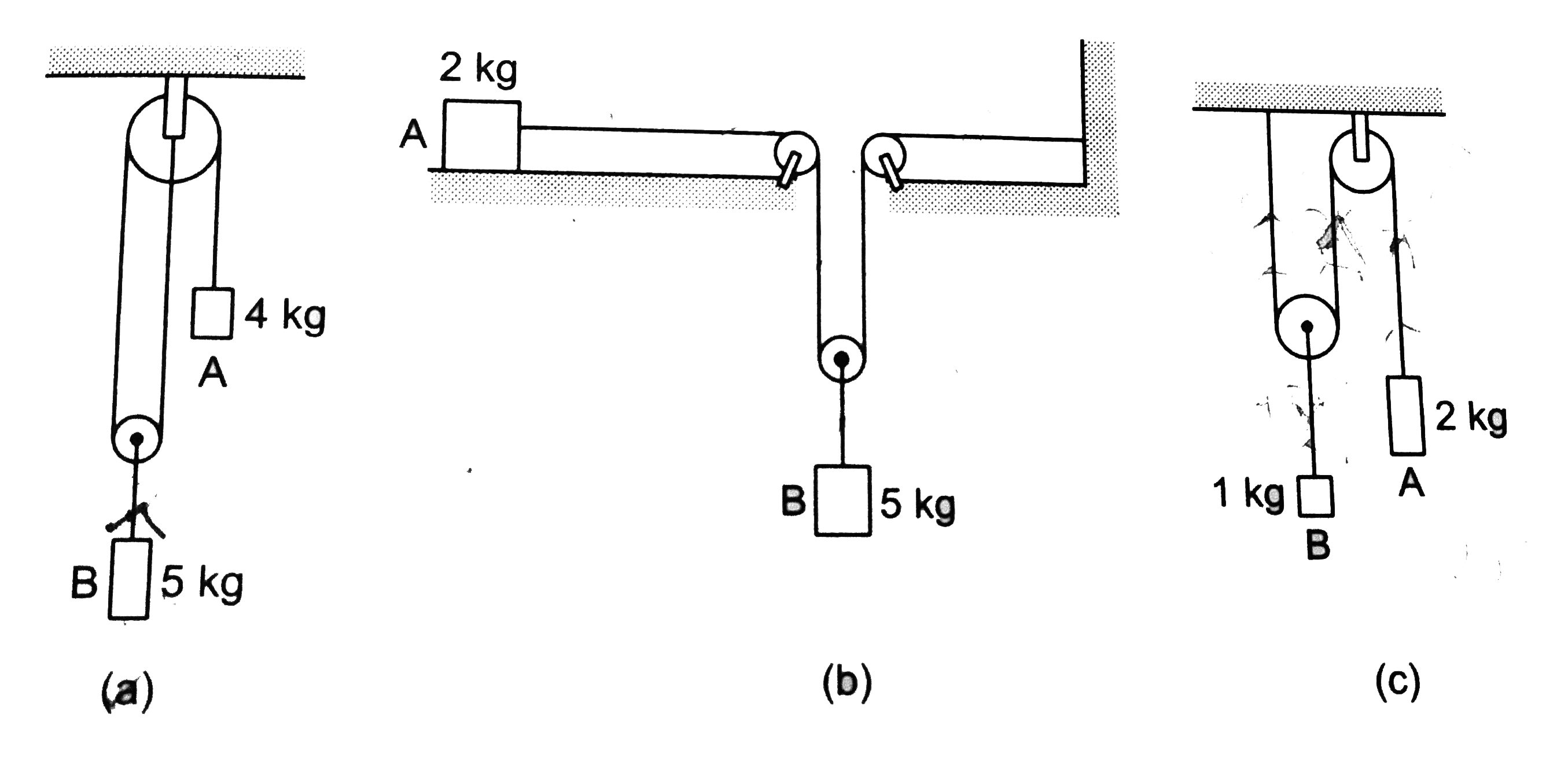
View SolutionFind the acceleration of the 500 g block in figure.
View SolutionA block of mass 'm' is kept on a smooth moving wedge. If the acceleration of the wedge is 'a'
View Solution
