An adiabatic piston of mass m equally divides an insulated container of total volume v0 and length l. A light spring connect the piston to right wall. The container has helium gas. The pressure on both side of piston is P0. The container starts moving with acceleration 'a' towards right, find the stretch of the spring when acceleration of the piston equals acceleration of container. (Assume displacement of the piston <<l)
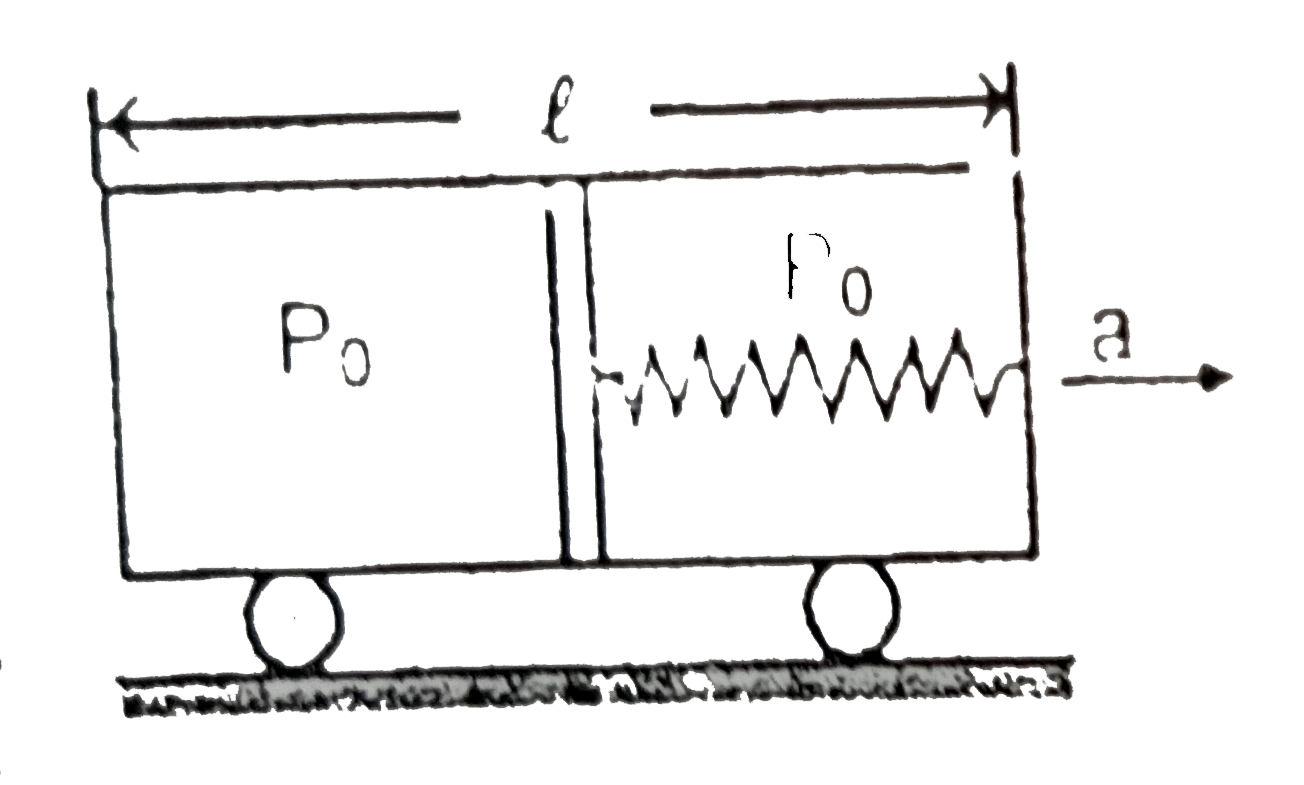
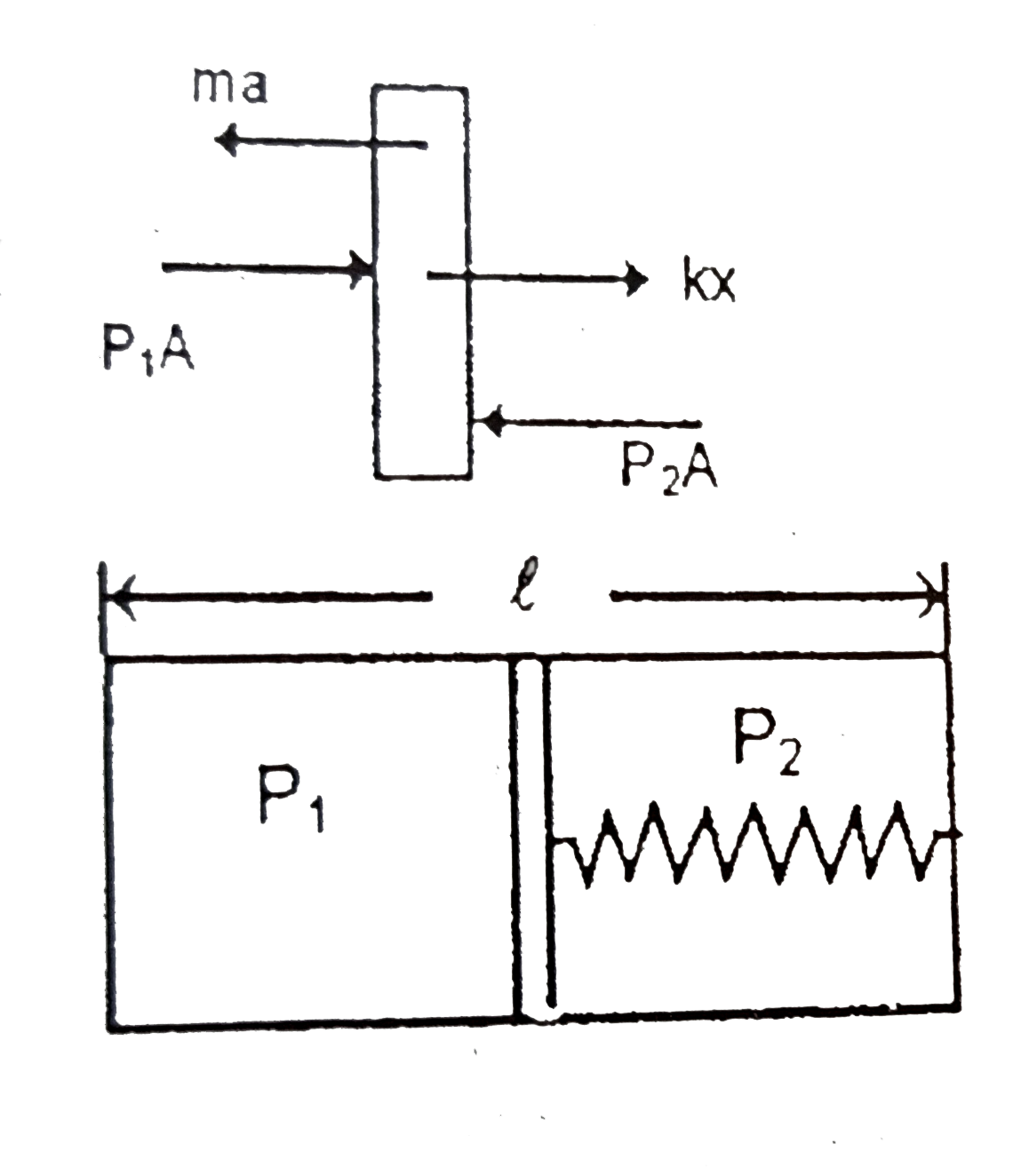
Free body diagram of the separator
P2A+ma=P1A+kx ….(1)
where A is the area of cross section of separator and x is the stretch of the spring
We can write
P0(V02)γ=P1(V02−Ax)γ …..(2)
and P0(V02)γ=P2(V02+Ax)γ ....(3)
from equation
P1=P0(V0(V0−2Ax))γ=P0(11−(2Ax/V0))γ
P1=P0(1−2AxA(l/2))−γ=P0(1+4xγl).......(4) (x<<l)
Similarly P2=P0(1−4xγl).....(5)
Substituting the values of P1 and P2 in equation (1)
P0(1−4xγl)A+ma=P0(1+4xγl)A+kx
[k+8γP0Al]x=ma
⇒x=⎡⎢⎣mak+8γP0V0l2⎤⎥⎦
Similar Questions
A smooth piston of mass m area of cross - section A is in equilibrium in a gas jar when the pressure of the gas is P0. Find the angular frequency of oscillation of the piston, assuming adiabatic Change of state of the gas.

View SolutionWhen the piston of common water pump is raised its piston valve opens.
View SolutionA fixed container is fitted with a piston which is attached to a spring of spring constant k. The other and of the spring is attached to a rigid wall. Initially the spring is in its natural length and the length of container between the piston and its side wall is L. Now an dideal diatomic gas is slowly filled in the container so that the piston moves quasistatically. It pushed the piston by x so that the spring now is compressed by x. The total rotaional kinetic energy of the gas molecules in terms of the displacement x of the piston is (there is vacuum outside the container)
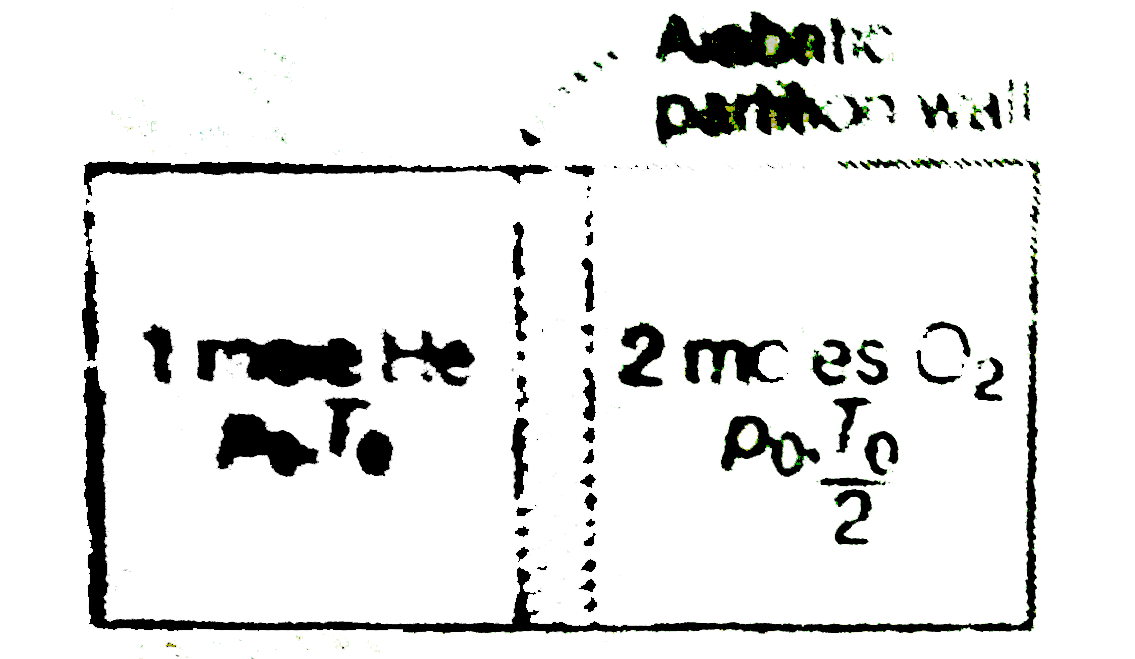
View SolutionConsider the adjacent figure. A piston divides a cylindrical container into two equal parts. The lets part contains 1 mole of helium gas and the right part contains two moles or oxygen gas. The initial temperatures and pressures of the gases in the left chamber are T0 and p0 and the right chamber are T02 and p0 respectively as shown in the figure. The piston as well as the walls of the container are adiabatic. After removal of the piston, gases mix homoganeously and the final pressure becomes p=4n13p0. Find the value of n.
View SolutionFigure shows initial state of an ideal gas trapped in a container with conducting walls and a piston (mass m) which can move without any friction. The container is placed on point supports and its wall are conducting. Assuming that atmospheric pressure is P0 and the mass of the ideal gas is negligible as compared to the mass of the piston and the mass of container. Take the cross section area of piston to be A. The piston is slowly lifted by an external agent and held in its position. Let M be the maximum mass of container so that it may "lift off" while pulling the piston upwards and Pi be the pressure of ideal gas in initial state. Pick the correct choice:

View SolutionA cylindrical vessel containing a liquid is closed by a smooth piston of mass m as shown in the figure. The area of cross section of the piston is A. If the atmospheric pressure is P0, find the pressure of the liquid just below the piston.
 ,
,
View SolutionA closed hollow insulated cylinder is filled with gas at 0∘C and also contains an insulated piston of negligible weight and negligible thickness at the middle point. The gas on one side of the piston is heated to 100∘C. If the piston moves 5cm the length of the hollow cylinder is
View SolutionA weightless piston divides a thermally insulated cylinder into two parts of volumes V and 3V.2 moles of an ideal gas at pressure P=2 atmosphere are confined to the part with volume V=1 litre. The remainder of the cylinder is evacuated. The piston is now released and the gas expands to fill the entire space of the cylinder. The piston is then pressed back to the initial position. Find the increase of internal energy in the process and final temperature of the gas. The ratio of the specific heats of the gas, γ=1.5.
View SolutionA cylidrical vesel containing a liquid is closed by a smooth piston of mass m as shown in the figure. The area of cross section of the piston is A. If the atmospheric pressure is P0, find the pressure of the liquid just below the piston.
 ,
,
View SolutionA piston of mass m divides a cylinder containing gas into two equal parts. Suppose the piston is displaced to the left to a distance x and let go Fig. Assuming the process to take place at a constant temperature, find the frequency of the piston's oscillations.
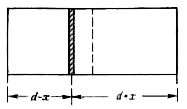
View Solution