Two identical rings, each of mass M and radius R, are standing on a rough horizontal surface. The rings overlap such that the horizontal line passing through their centre makes an angle of θ=45∘ with the radius through their intersection point P. A small object of mass m is placed symmetrically on the rings at point P and released. Calculate the acceleration of the centre of the ring immediately after the release. There is no friction between the small object and the rings. The friction between the small object and the rings, and the friction between the rings and the ground is large enough to prevent slipping.
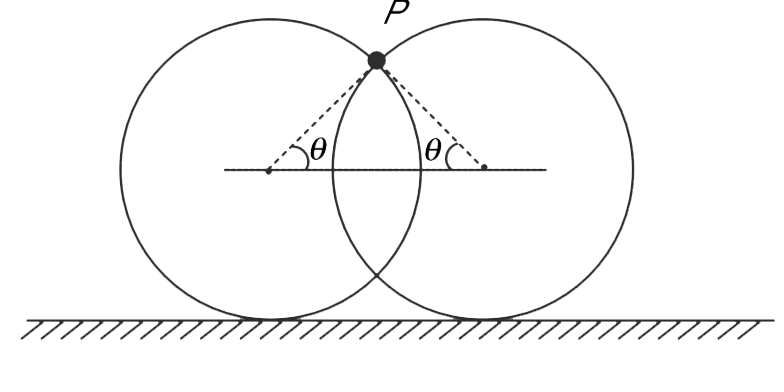
The correct Answer is:mg4M+m
Step by step video, text & image solution for Two identical rings, each of mass M and radius R, are standing on a rough horizontal surface. The rings overlap such that the horizontal line passing through their centre makes an angle of theta = 45^(@) with the radius through their intersection point P. A small object of mass m is placed symmetrically on the rings at point P and released. Calculate the acceleration of the centre of the ring immediately after the release. There is no friction between the small object and the rings. The friction between the small object and the rings, and the friction between the rings and the ground is large enough to prevent slipping. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
Similar Questions
From a ring of mass M and radius R, a 30o sector is removed. The moment of inertia of the remaining portion of the ring, about an axis passing through the centre and perpendicular to the plane of the ring is
View Solution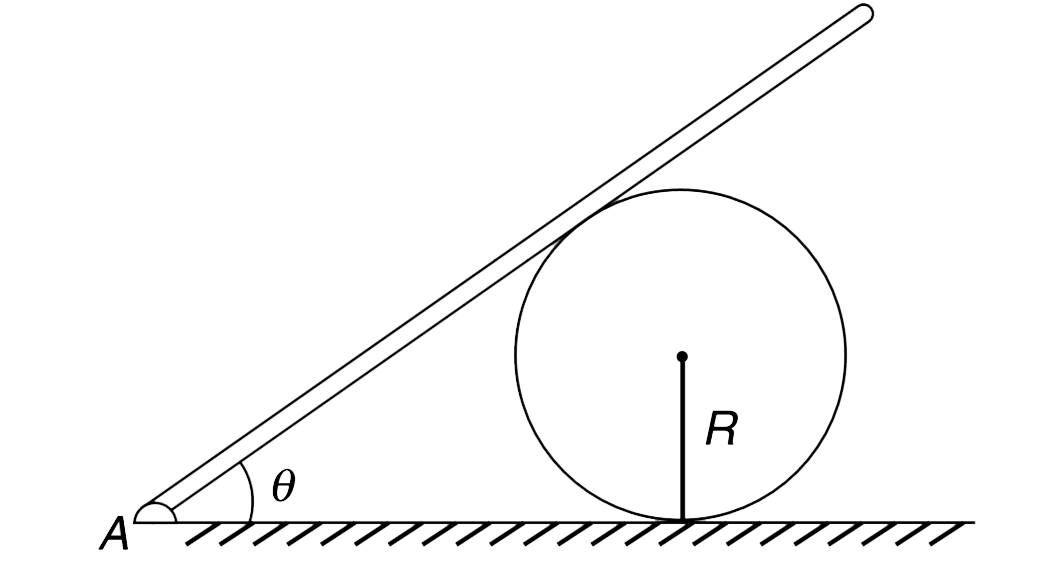
A ring of mass M and radius R is held at rest on a rough horizontal surface. A rod of mass M and length L=2√3R is pivoted at its end A on the horizontal surface and is supported by the ring. There is no friction between the ring and the rod. The ring is released from this position. Find the acceleration of the ring immediately after the release if θ=60∘. Assume that friction between the ring on the horizontal surface is large enough to prevent slipping of the ring.View Solution
Knowledge Check
- Question 1 - Select One
For a uniform ring of mass M and radius R at its centre
Afield and potential both are zeroBfield is zero but potential is GMRCfield is zero but potential is −GM/RDmagnitude of field is GMR2 and potential −GMR - Question 2 - Select One
Find the moment of inortia of ring of mass m and radius R about an axis passing through its centre and making an angle of 45∘ with its plane:
 AMR24BMR22C34MR2DMR2
AMR24BMR22C34MR2DMR2 - Question 3 - Select One
A ring of mass m and radius R rolls on a horizontal roudh surface without slipping due to an applied force 'F'. The frcition force acting on ring is :−
 AF3B2F3CF4DZero
AF3B2F3CF4DZero
A thin ring of mass m and radius R is in pure rolling over a horizontal surface. If v0 is the velocity of the centre of mass of the ring, then the angular momentum of the ring about the point of contact is
View SolutionTwo identical concentric rings each of mass m and radius R are placed perpendicularly. What is the moment of inertia of the system about the axis of one of the rings ?
View SolutionFrom a complete ring of mass M and radius R, a 30∘sector is removed. The moment of inertia of the incomplete ring about an axis passing through the centre of the ring and perpendicular to the plane of the ring is
 ,View Solution
,View SolutionA force F is applied at the top of a ring of mass M and radius R placed on a rough horizontal surface as shown in figure. Friction is sufficient to prevent slipping. The friction force acting on the ring is:
 View Solution
View SolutionMoment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
View Solution

