Question

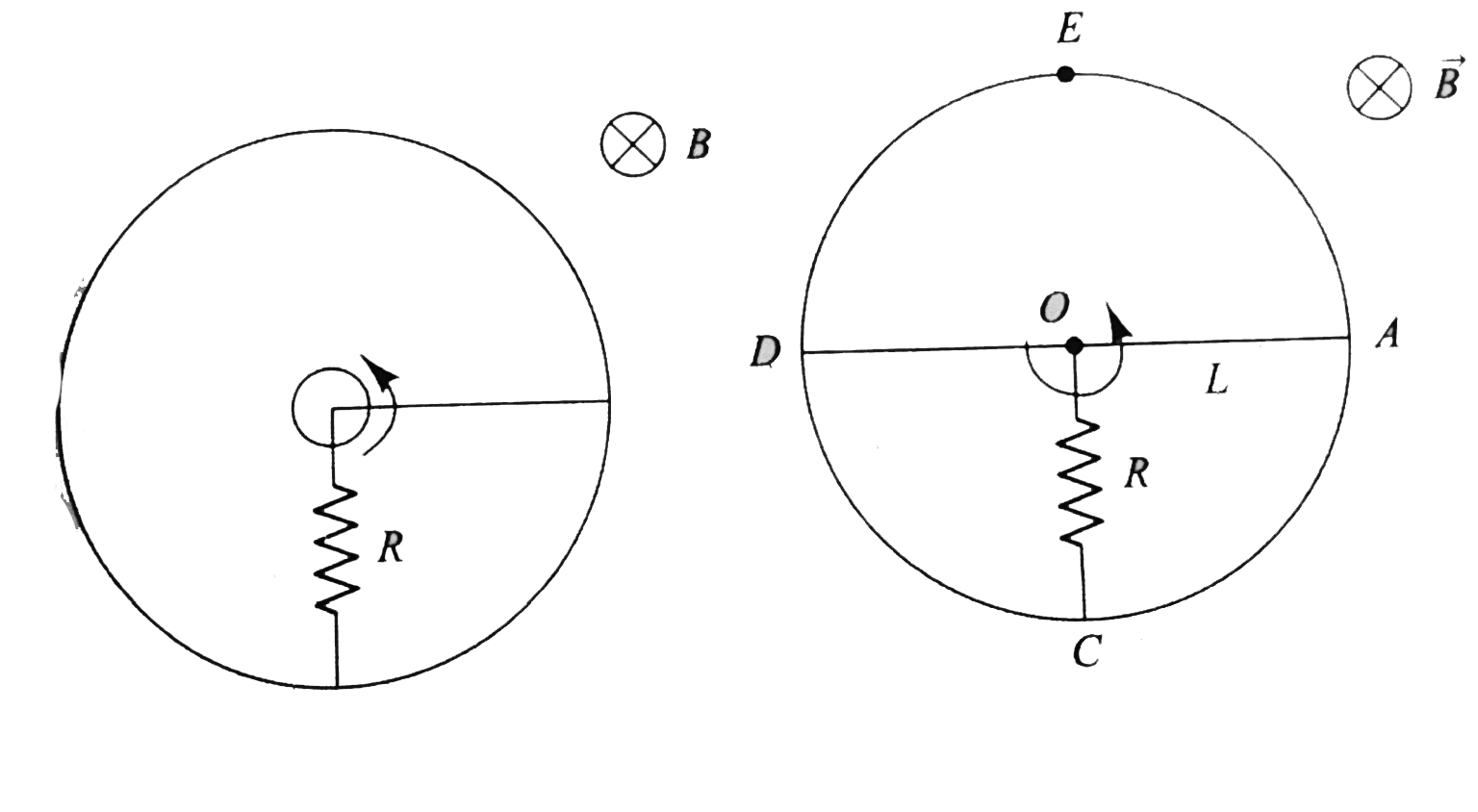
A metallic disc of radius $r$ is made of a material of negligible resistance and can rotate about a conducting horizontal shaft. A smaller non conducting disc of radius a is fixed onto the same shaft and has a massless cord wrapped around it, which is attached to a small object of mass $m$ as shown. Two ends of a resistor of resistance $R$ are connected to the perimeter of the disc and to the shaft by sliding contacts. The system is then placed into a uniform horizontal magnetic field $B$ and the mass $m$ is released. Find the terminal angular velocity with which the disc will rotate finally.
(Take $r=10cm$, $a=2cm$, $R=\frac{1}{100}\Omega$, $B=0.2T$, $m=50gm$, $g=10m/s^2$)

Options

A. `200 rad//s`
B. `300 rad//s`
C. `100 rad//s`
D. `10 rad//s`

Explanation

At terminal stage, torque applied on the smaller disc by the rope `=mga`
current to the disc `=(Bomega r^(2))/(2R)`(where `omega` is terminal angular velocity)
torque applied by magnetic field `=(B^(2)omega r^(4))/(4R)`
So, `(B^(2)omega r^(4))/(4R)=mga`
`omega=100 rad//sec`