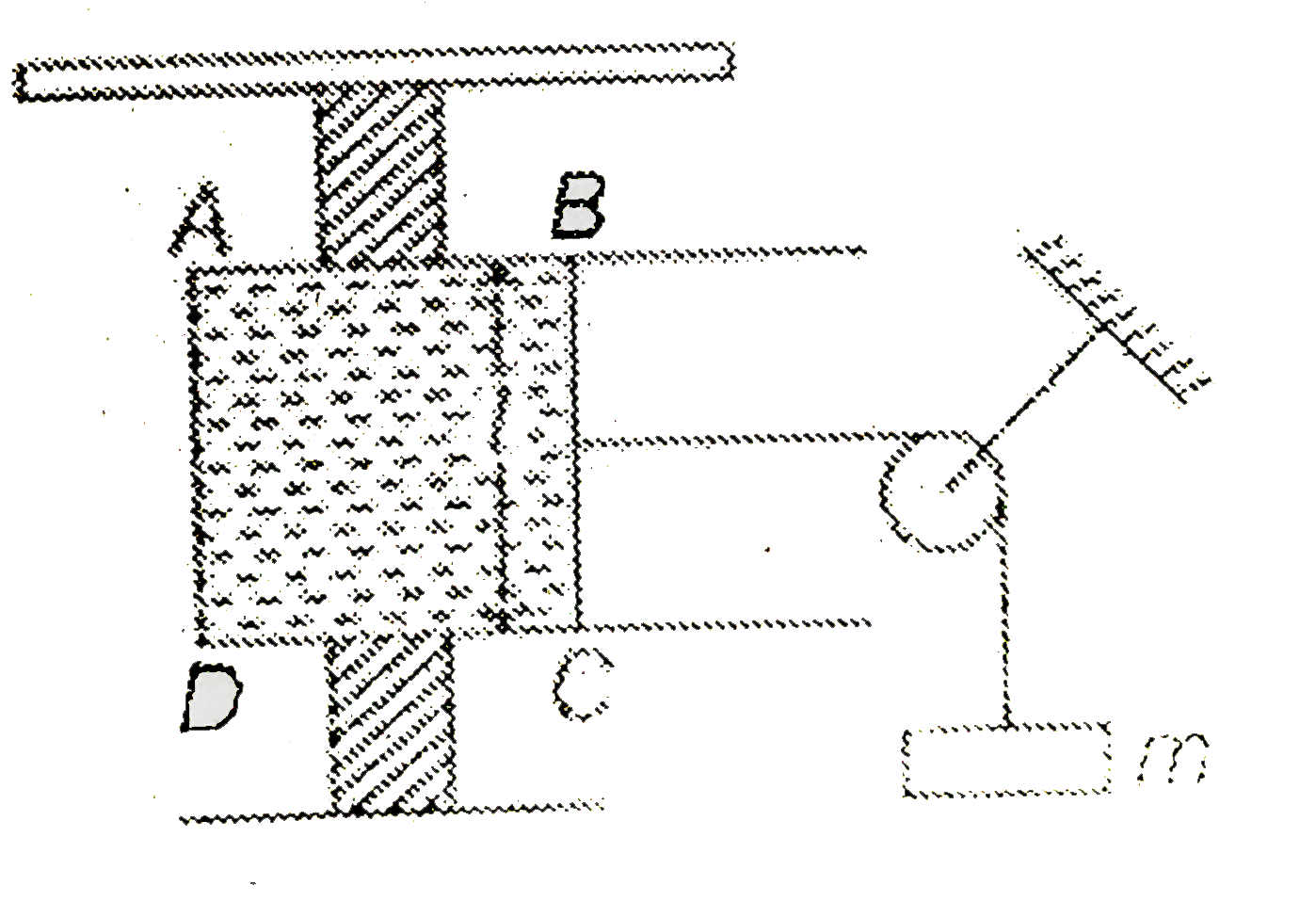
The two indentical rectangular stell frames with the dimensions shown are farbricted from a bar of the same material and are hinged. Rectangular at the midpoints A and B of their side (3m×1m). If the frame is resting in the position shown on a horizontal surface with negligible friction, determine the velocity v with which each of the upper ends of the frame hits the horizontal surface if the cord D is cut. (Take the value of dimensions shown in the figure c=1m, b=3/2m and θ=174∘ i.e., sinθ2=35 and cosθ2=45 & g=10m/s2)

5m/s
8m/s
3m/s
4m/s
Let the mass per unit length of the bar be λ(kg/m)
As the frames come down, the point B moves vertically downwards and PP' remain in contact with the ground. In the final state (when PQ, P'Q' just become horizontal), the velocitites of P (and P') is zero. The vertical component was already zero, the horizontal component also becomes zero. The motion of PQ is essentially rotation about P at that instant. Conservation of mechanical energy gives (for PQ) :
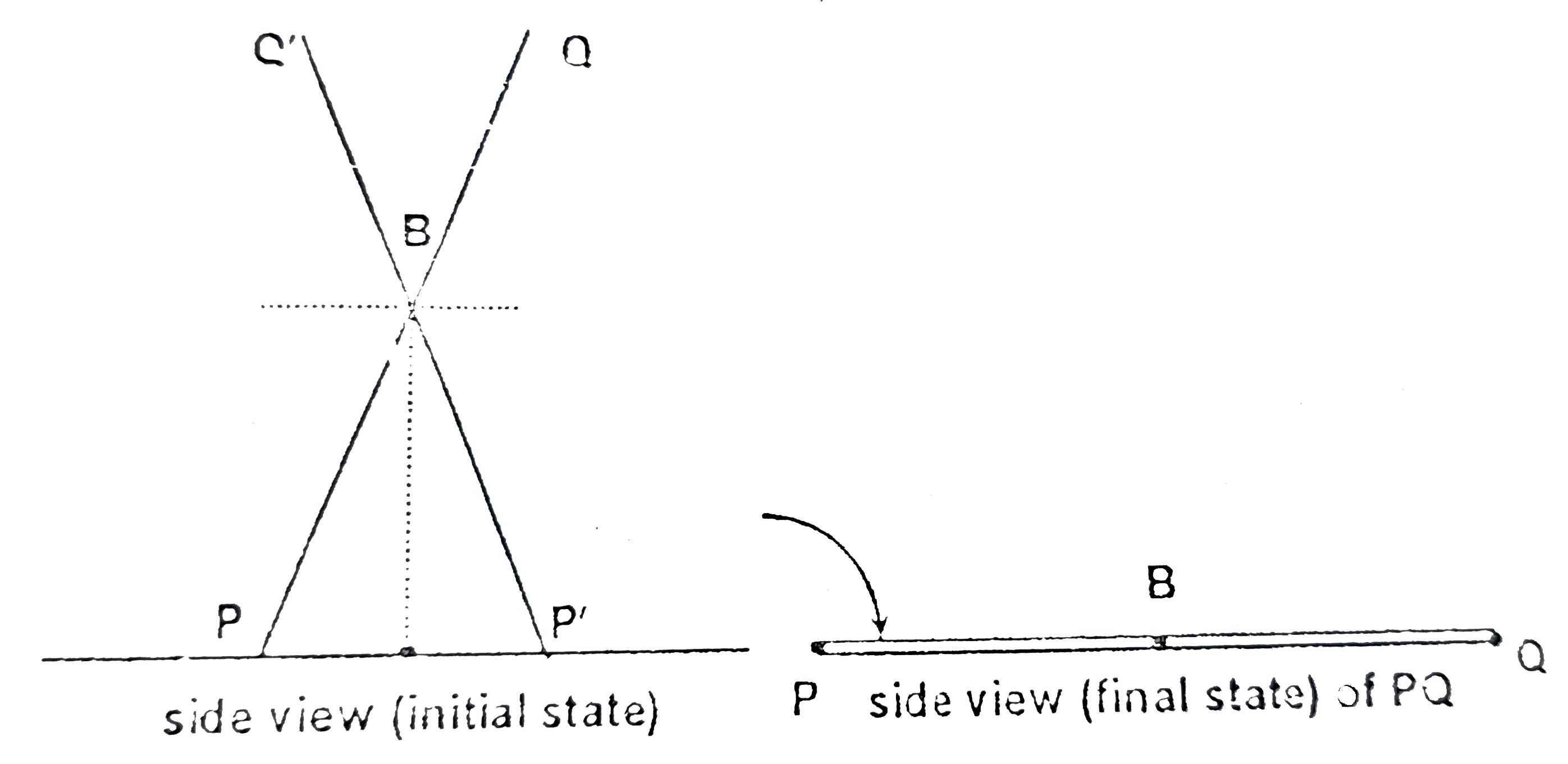
(2λ+6λ)g(3)2cos37∘=12(13⋅6λ⋅32+λ⋅32)ω2
and vQ=ω⋅PQ=ω×3=8m/s
Similar Questions
Write the vector representation of the vectors A and B with respect to the frame of reference shown in the figure.

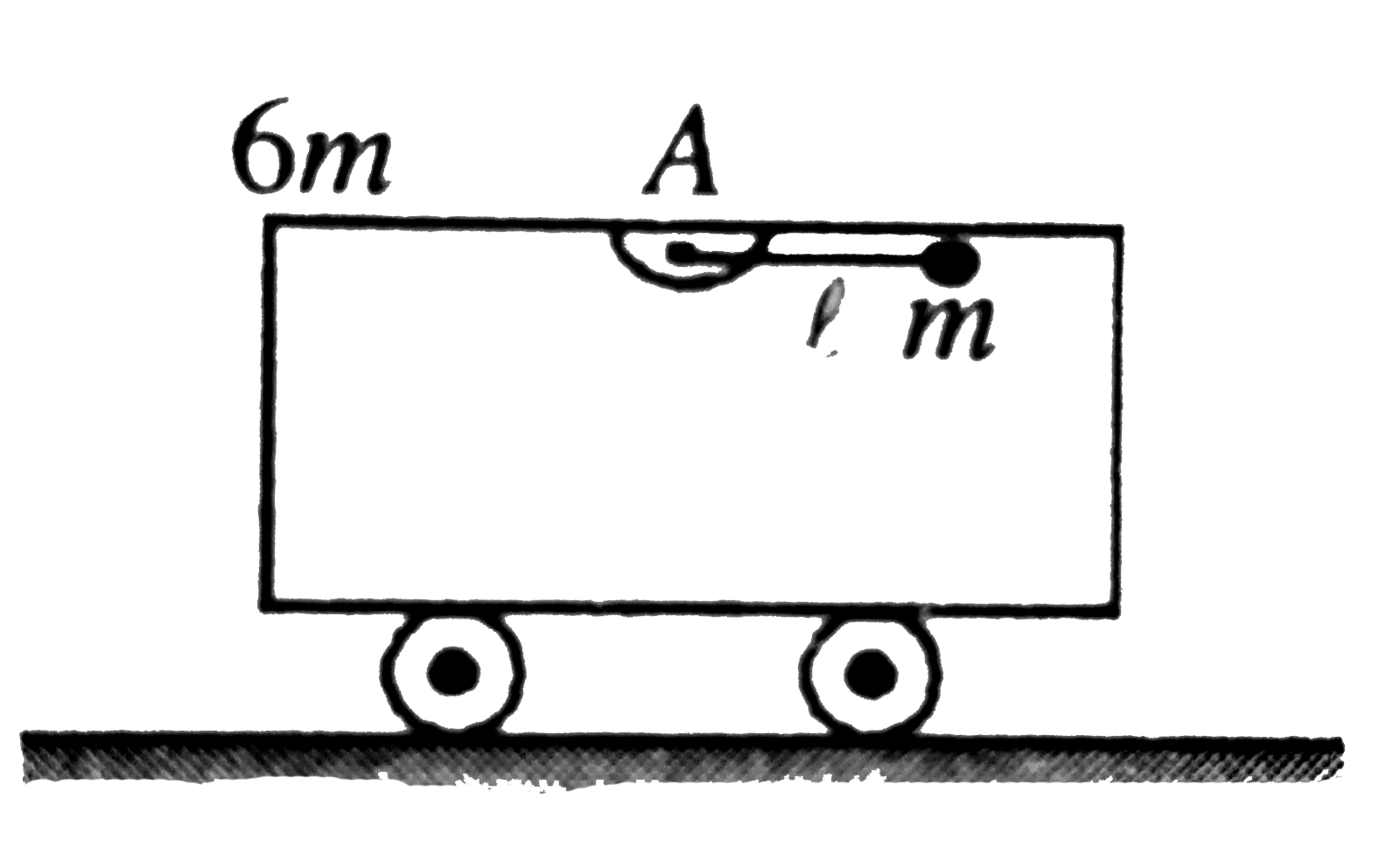
View SolutionIn the figure shown, the cart of mass 6m is initially at rest. A particle of mass in is attached to the end of the light rod which can rotate freely about A. If the rod is released from rest in a horizontal position shown, determine the velocity vrel of the particle with respect to the cart when the rod is vertical.
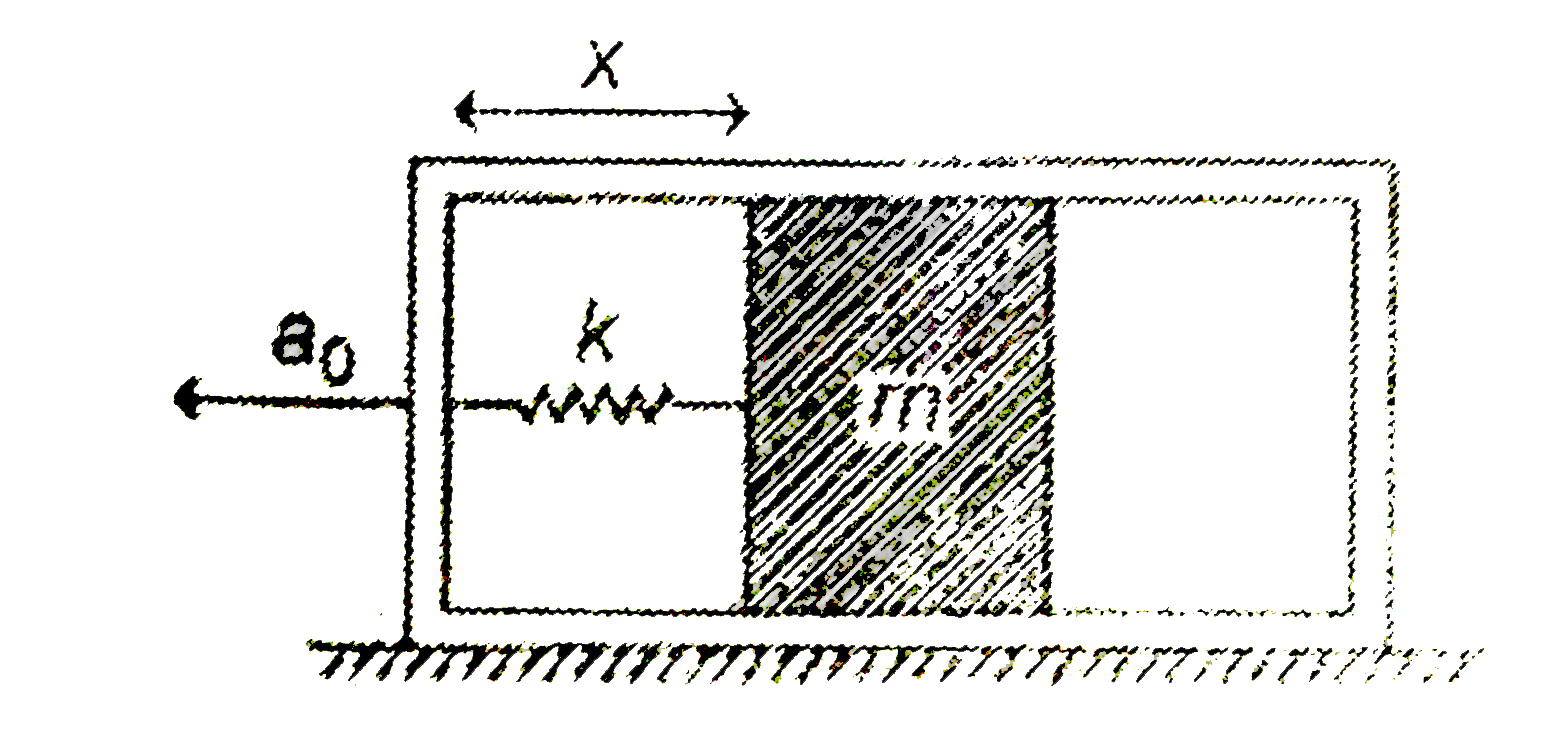
View SolutionA block of mass m is attached to a frame by a light spring of force constant k. The frame and block are initially at rest with x=x0, the natural length of the spring. If the frame is given a constant horizontal accelration a0 towards left, determine the maximum velocity of the block relative to the frame (block is free to move inside frame). Ignore any friction.
View SolutionA block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. The maximum compression in spring is

View SolutionA solenoid wound over a rectangular frame. If all the linear dimensions of the frame are increased by a factor 3 and he number of turns per unit length remains the same, the self inductance increased by a factor of
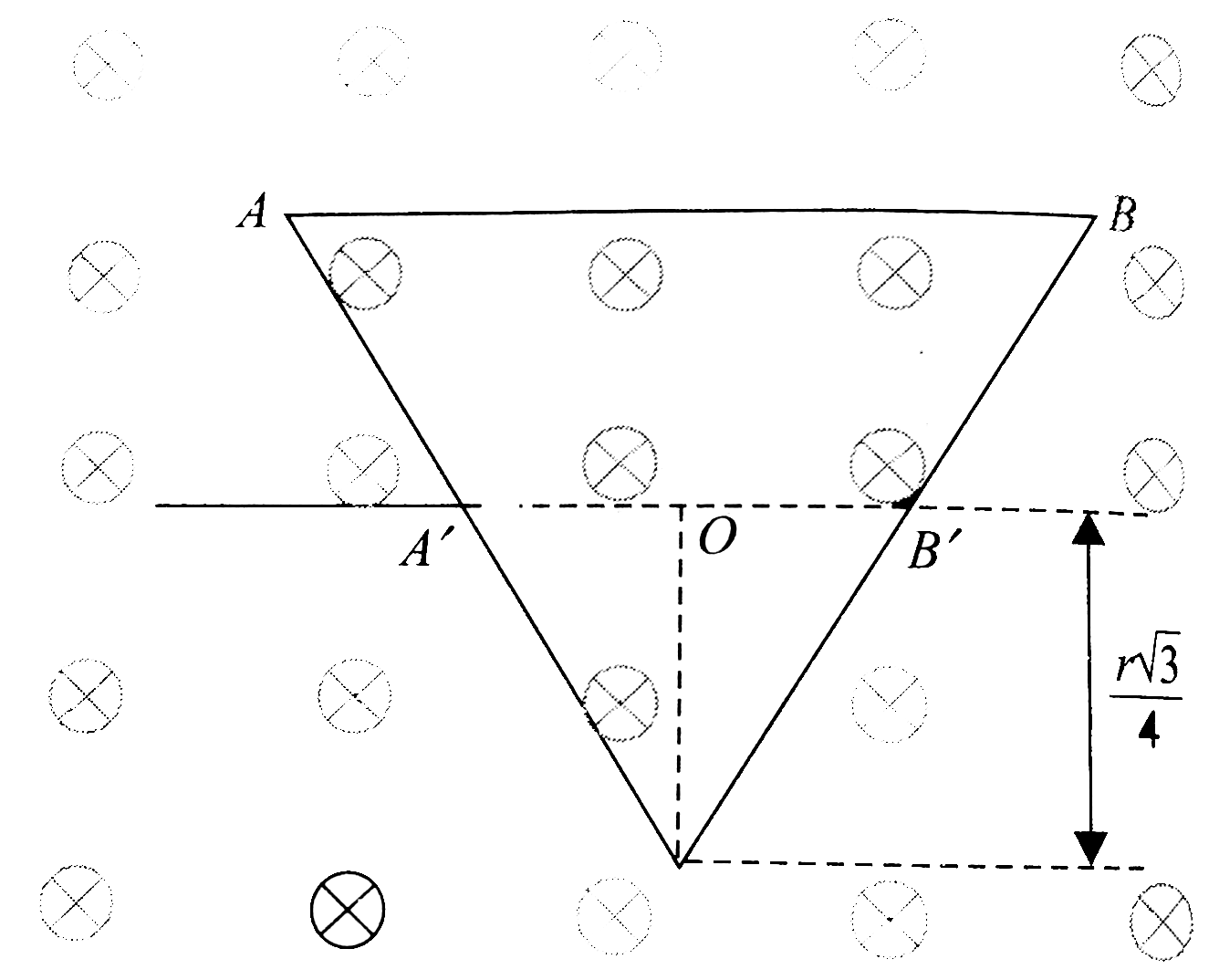
View SolutionABC is an equilateral triangular frame of mass m and side r. It is at rest under the action of horizontal magnetic field B (as shown) and the gravitational field.
View SolutionA wire frame ABCD has a soap film. The wire BC can slide on the frame without friction and it is in equilibrium in the position shown in the figure. Find m, if T is the surface tension of the liquid.
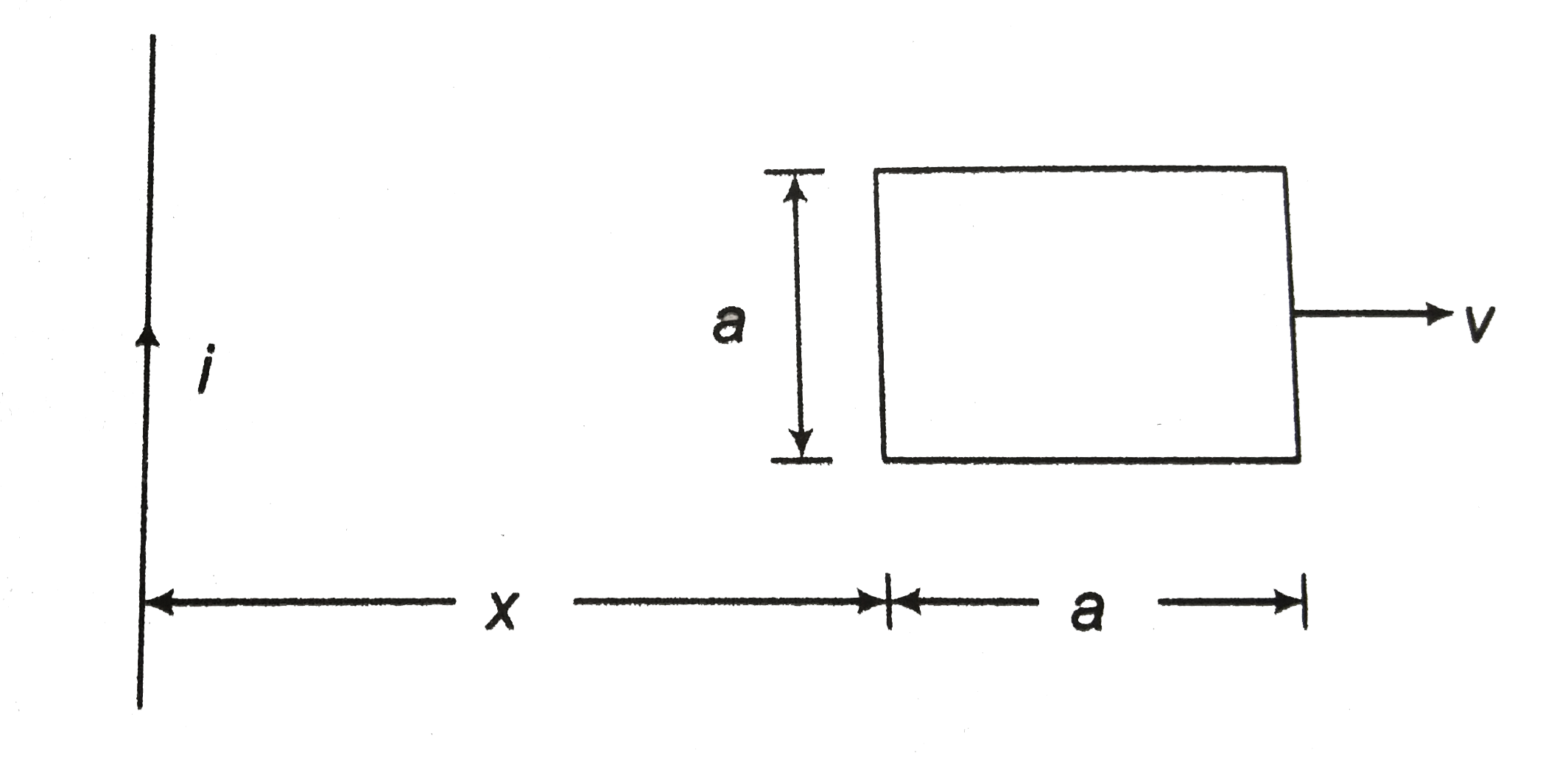
View SolutionA square frame with side a and a long straight wire carrying a current i are located in the same plane as m shown in figure. The fram translates to the right with a constant velocity v. Find the emf induced in the frame as a function of distance x.
View SolutionConsider a block of mass 10kg. which rests on as smooth surface and is subjected to a horizontal force of 6N. If observer A is in a fixed frame x.
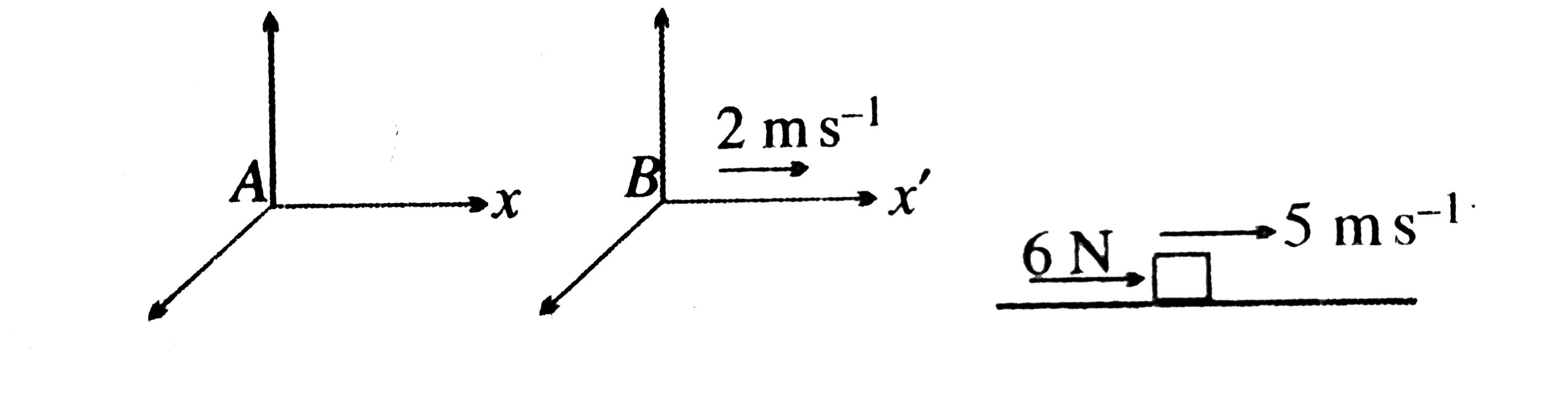
View SolutionA cylinder is rolling towards a cube of same mass on rough horizontal surface ( coefficient of friction = μ) with velocity v0 as shown in figure. Assume elastic collision and friction is negligible between cube and cylinder. Then after collision

View Solution
