A steady current is flowing in a circular coil of radius R, made up of a thin conducting wire. The magnetic field at the centre of the loop is BL. Now, a circular loop of radius R/n is made from the same wire without changing its length, by unfounding and refolding the loop, and the same current is passed through it. If new magnetic field at the centre of the coil is BC, then the ratio BL/BC is
1:n2
1:L
n:n2
n:n1/2
To solve the problem, we need to find the ratio of the magnetic fields BLBC at the center of two circular loops made from the same wire but with different radii.
1. Magnetic Field at the Center of the Original Loop (B_L):
The magnetic field at the center of a circular loop of radius R carrying a current I is given by the formula:
BL=μ0I2R
where μ0 is the permeability of free space.
2. Length of the Wire:
The length of the wire used to make the original loop is:
L=2πR
3. New Loop with Radius Rn:
When the wire is refolded to form a new loop of radius Rn, the length of the wire remains the same. The circumference of the new loop is:
L′=2π(Rn)=2πRn
4. Number of Turns (n):
Since the length of the wire remains constant, we can find the number of turns n in the new loop:
n=LL′=2πR2πRn=n
5. Magnetic Field at the Center of the New Loop (B_C):
The magnetic field at the center of the new loop with n turns and radius Rn is given by:
BC=nμ0I2(Rn)=n2μ0I2R
6. Finding the Ratio BLBC:
Now we can find the ratio of the two magnetic fields:
BLBC=μ0I2Rn2μ0I2R=1n2
Final Result:
Thus, the ratio BLBC is:
BLBC=1n2
The magnetic field at the center of a circular loop of radius R carrying a current I is given by the formula:
BL=μ0I2R
where μ0 is the permeability of free space.
The length of the wire used to make the original loop is:
L=2πR
When the wire is refolded to form a new loop of radius Rn, the length of the wire remains the same. The circumference of the new loop is:
L′=2π(Rn)=2πRn
Since the length of the wire remains constant, we can find the number of turns n in the new loop:
n=LL′=2πR2πRn=n
The magnetic field at the center of the new loop with n turns and radius Rn is given by:
BC=nμ0I2(Rn)=n2μ0I2R
Now we can find the ratio of the two magnetic fields:
BLBC=μ0I2Rn2μ0I2R=1n2
Thus, the ratio BLBC is:
BLBC=1n2
Similar Questions
A circular coil of n turns and radius r carries a current I. The magnetic field at the centre is
View SolutionA square loop of side a carris a current I. The magnetic field at the centre of the loop is
View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is
 View Solution
View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is :
 View Solution
View SolutionA current I flows along a triangle loop having sides of equal length a. The strength of magnetic field at the centre of the loop is :
 View Solution
View SolutionA square conducting loop of side length L carries a current I.The magnetic field at the centre of the loop is
View SolutionWhat will be magnetic field at centre of current carrying circular loop of radius R?
View SolutionA rectangular loop of metallic wire is of length a and breadth b and carries a current i. The magnetic field at the centre of the loop is
View SolutionA current I flows along a round circular loop of radius R. Find the line integration of magnetic field along the axis of the loop from center to ∞
View SolutionA current l flows through a closed loop as shown in figure .The magnetic field at the centre O is
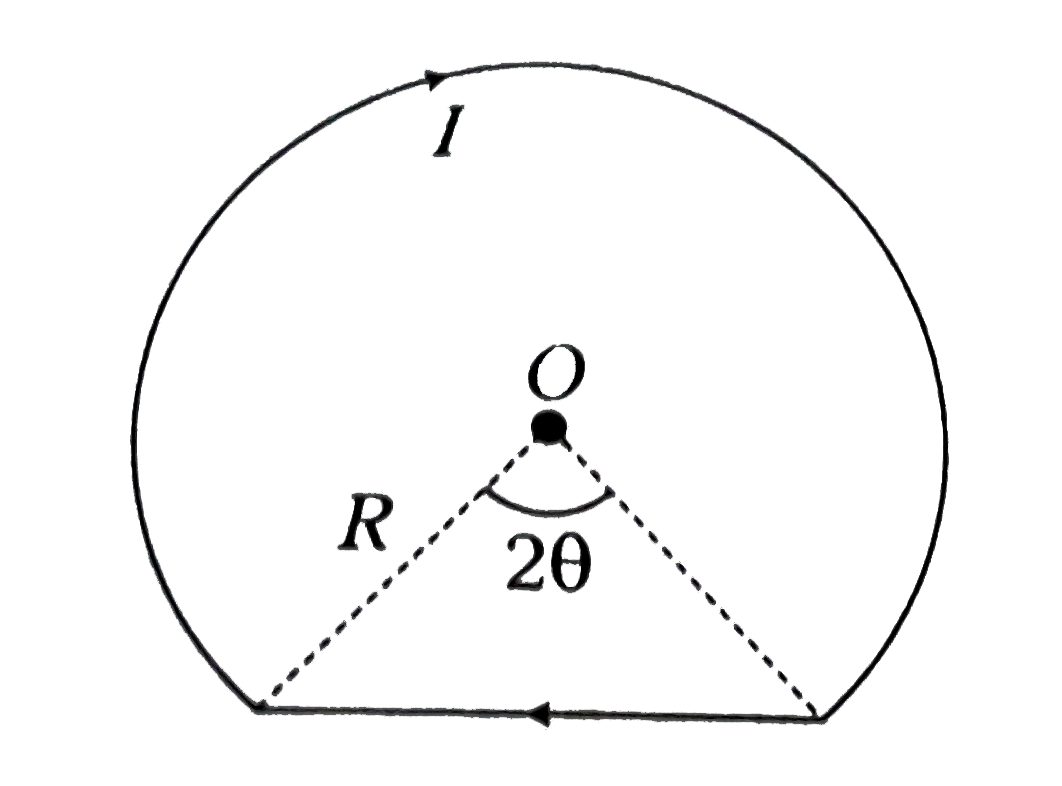 View Solution
View Solution

