A thick rope of length 2L and linear mass density 9μ is joined at B to a thin rope of length L and linear mass density 4μ. The systems horizontally stretched by the two vertical wall A and C. Assuming B to be a node, find the minimum number of loops in the thick rope.

1
2
3
4
2L=m×(λ1/2)=m2f√T9μ
L=n×(λ2√2)=n2f√T4μ
⇒m=3n=3×1=3
Similar Questions
One end of a horizontal thick copper wire of length 2L and radius 2R is weded to an end of another horizontal thin copper wire of length L and radius R .When the arrangement is stretched by applying forces at two ends , the ratio of the elongation in the thin wire to that in the thick wire is
View SolutionA thin wire of length L and uniform linear mass density ρ is bent into a circular loop with centre at O as shown. The moment of inertia of the loop about the axis XX' is
View Solution
Knowledge Check
- Question 1 - Select One
One end of a horizontal thick copper wire of length 2L and radius 2R is welded to an end fo another horizontal thin copper wire of lenth L and radius R. When the arrangement is stretched by applying forces at two ends, the ratio of the elongation in the thin wire to that in the thick wire is
A0.25BÂ 0.50CÂ 2.00D4.00
A rope of length l and mass 'm' is connected to a chain of length l and mass 2m and hung vertically as shown. What is the change in graviational potential energy if the system is inverted and hung from same point.
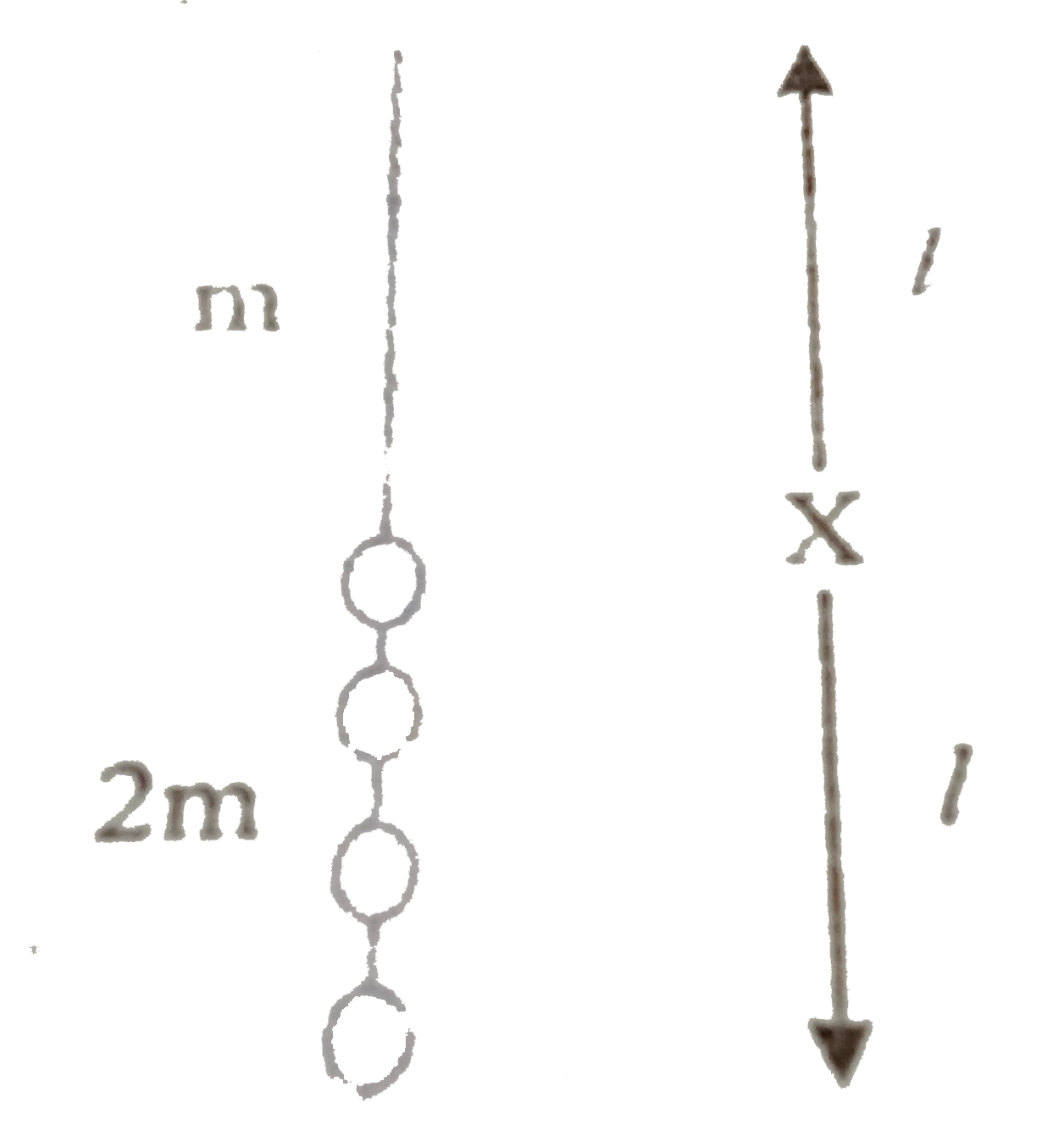 .View Solution
.View SolutionTwo uniform thin rods each of length L and mass m are joined as shown in the figure. Find the distance of centre of mass the system from point O
 View Solution
View SolutionFind coordinates of mass center of a non-uniform rod of length L whose linear mass density lambda varies as lambda=a+bx, where x is the distance from the lighter end.
View SolutionYou are given a rod of length L. The linear mass density is λ such that λ=a+bx. Here a and b are constants and the mass of the rod increases as x decreases. Find the mass of the rod
 View Solution
View SolutionA wire of length 2.00 m is stretched to a tension of 160 N. If the fundamental frequency of vibration is 100 Hz, find its linear mass density.
View SolutionTwo ropes of length l and l/2 and mass per unit length μandμ/4 respectively are joined at B and hanged vertically with a heavy mass at its end C. A pulse is generated simultaneously at both ends A and C which travels along the ropes. Find the distance from the top at which pulses will cross each other.
View SolutionA uniform thin rod AB of length L has linear mass density μ(x)=a+bxL, where x is measured from A. If the CM of the rod lies at a distance of (712L) from A, then a and b are related as :_
View Solution

