Two ropes of length l and l/2 and mass per unit length μandμ/4 respectively are joined at B and hanged vertically with a heavy mass at its end C. A pulse is generated simultaneously at both ends A and C which travels along the ropes. Find the distance from the top at which pulses will cross each other.
The correct Answer is:5l8
To solve the problem of finding the distance from the top at which the pulses will cross each other, we can follow these steps:
Step 1: Understand the Setup
We have two ropes:
- Rope 1 (upper rope) has length L and mass per unit length μ.
- Rope 2 (lower rope) has length L2 and mass per unit length μ4.
Both ropes are joined at point B and hang vertically with a heavy mass at point C.
Step 2: Determine the Velocities of the Pulses
The velocity of a pulse traveling through a rope is given by the formula:
v=√Tμ
where T is the tension in the rope and μ is the mass per unit length.
- For the upper rope (length L):
v1=√Tμ
- For the lower rope (length L2):
v2=
⎷Tμ4=√4Tμ=2√Tμ=2v1
Thus, the velocity of the pulse in the lower rope is twice that of the upper rope.
Step 3: Calculate the Time Taken for Pulses to Reach Point B
Let t be the time taken for the pulse from point C to reach point B. The distance from C to B is L2.
Using the velocity of the lower rope:
t=DistanceVelocity=L2v2=L22v1=L4v1
Step 4: Calculate the Distance Travelled by the Upper Pulse in Time t
During the time t, the pulse from point A will travel a distance d1 in the upper rope:
d1=v1⋅t=v1⋅L4v1=L4
Step 5: Determine the Position of the Pulses
- The pulse from point C reaches point B after time t.
- The pulse from point A travels L4 downwards in the same time.
Step 6: Find the Meeting Point
At the time the pulse from C reaches B, the pulse from A has traveled L4 downwards. The total distance from the top of the upper rope to the meeting point is:
Distance from top=L4+Distance from B to meeting point
Since the total length of the upper rope is L, the distance from B to the top of the upper rope is:
L−L4=3L4
Step 7: Calculate the Final Meeting Point
The pulses meet at:
Distance from top=L4+3L4=L
However, since we need the distance from the top where they cross, we take the midpoint of their meeting:
Meeting Point=L4+L4=L2
Final Answer
The distance from the top at which the two pulses will meet is:
5L8
We have two ropes:
- Rope 1 (upper rope) has length L and mass per unit length μ.
- Rope 2 (lower rope) has length L2 and mass per unit length μ4.
Both ropes are joined at point B and hang vertically with a heavy mass at point C.
The velocity of a pulse traveling through a rope is given by the formula:
v=√Tμ
where T is the tension in the rope and μ is the mass per unit length.
v1=√Tμ
v2=
⎷Tμ4=√4Tμ=2√Tμ=2v1
Thus, the velocity of the pulse in the lower rope is twice that of the upper rope.
Let t be the time taken for the pulse from point C to reach point B. The distance from C to B is L2.
t=DistanceVelocity=L2v2=L22v1=L4v1
During the time t, the pulse from point A will travel a distance d1 in the upper rope:
d1=v1⋅t=v1⋅L4v1=L4
- The pulse from point C reaches point B after time t.
- The pulse from point A travels L4 downwards in the same time.
At the time the pulse from C reaches B, the pulse from A has traveled L4 downwards. The total distance from the top of the upper rope to the meeting point is:
Distance from top=L4+Distance from B to meeting point
Since the total length of the upper rope is L, the distance from B to the top of the upper rope is:
L−L4=3L4
The pulses meet at:
Distance from top=L4+3L4=L
However, since we need the distance from the top where they cross, we take the midpoint of their meeting:
Meeting Point=L4+L4=L2
The distance from the top at which the two pulses will meet is:
5L8
Topper's Solved these Questions
- WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - Assignment (Section-J) (Subjective Type Questions)
5 Videos
- WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - Assignment (Section-J) (Paragraph Type Questions)
4 Videos
- WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - Assignment (Section-H) (Mutiple true-false type questions)
3 Videos
- WAVE OPTICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assignment (Section-J (Aakash Challengers question))
1 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - D)
13 Videos
Similar Questions
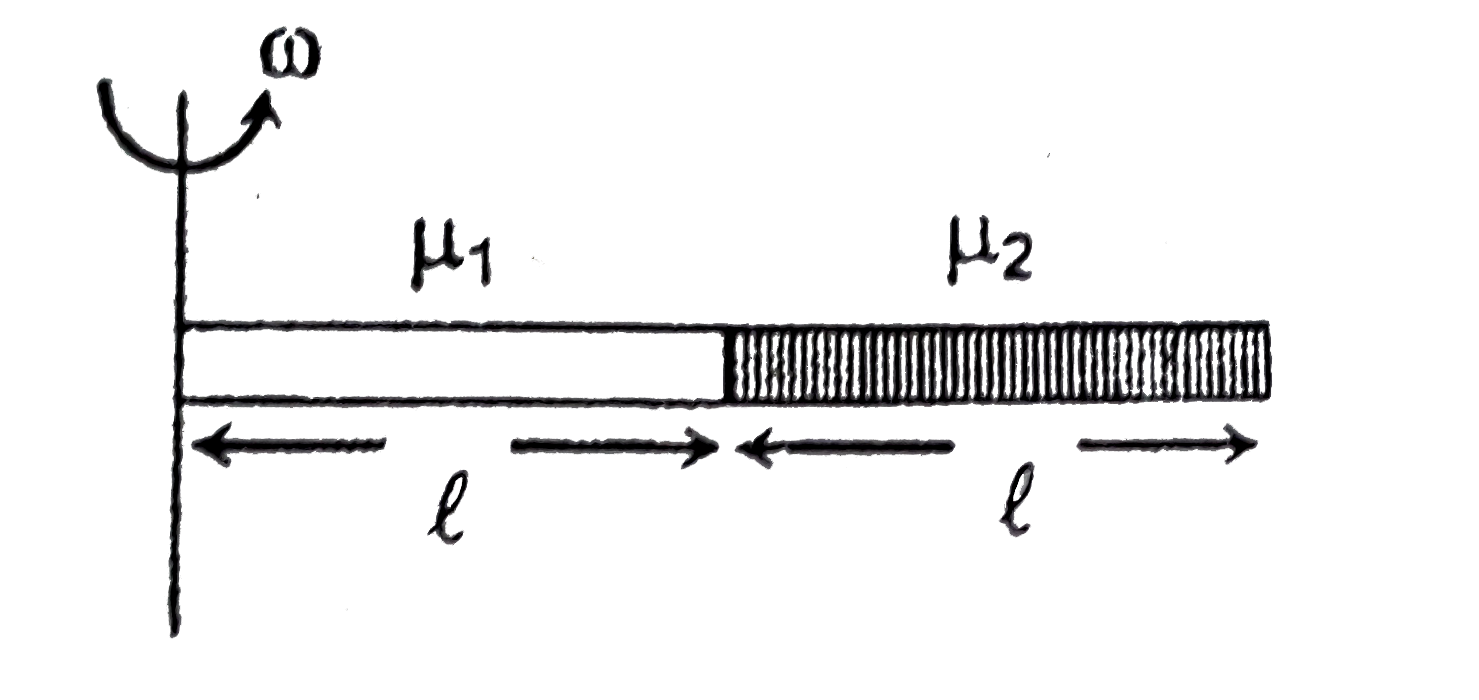
Two thin rods of same length l but of different uniform mass per unit length μ1 and μ2 respectively are joined together. The system is ortated on smooth horizontal plane as shown in figure. The tension at the joint will be
View SolutionA wire of length L, is hanging vertically from a rigid support. If a transverse wave pulse is generated at the free end of wire then which of the following statement is wrong
View SolutionTwo uniform thin rods each of length L and mass m are joined as shown in the figure. Find the distance of centre of mass the system from point O

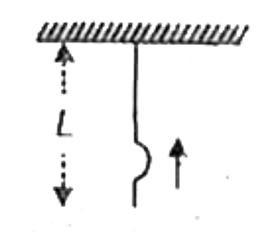
View SolutionA pulse is generated at lower end to a hanging rope of uniform density and length L. The speed of the pulse when it reaches the mid point of rope is
View SolutionA thick rope of length 2L and linear mass density 9μ is joined at B to a thin rope of length L and linear mass density 4μ. The systems horizontally stretched by the two vertical wall A and C. Assuming B to be a node, find the minimum number of loops in the thick rope.

View SolutionA thin bar of length L has a mass per unit length λ, that increases linerarly with distance from one end. If its total mass is M and its mass per unit length at the lighter end is λ0, then the distance of the centre of mass from the lighter end is
View SolutionA non-uniform rope of length l hangs from a ceiling.Mass per unit length of rope (μ) changes as μ=μ0ey, where y is the distance along the string from its lowest point.Then graph between square of velocity of wave and y will be best represented as :

View SolutionA wire of variable mass per unit length μ=μ0x, is hanging from the ceiling as shown in figure. The length of wire is l0 . A small transverse disturbance is produced at its lower end. Find the time after which the disturbance will reach to the other ends.
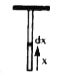
View SolutionA uniform rope of mass m per unit length, hangs vertically from a support so that the lower end just touches the table top shown in figure. If it is released, show that at the time a length y of the rope has fallen, the force on the table is equivalent to the weight of the length 3y of the rope.

View SolutionA chain of mass M and length L is held vertical by fixing its upper end to a rigid support. The tension in the chain at a distance y from the rigid support is:
View Solution
