Statement-1 : It is not necessary for a particle to move in a circular path to define angular momentum. It can be defined about any point in space.
Statement-2 : Particle moving in a straight line has non-zero angular momentum about a point which is not lying on the path of the particle.
Statement-1 is True, Statement-2 is True, Statement-2 is a correct explantion for Statement-1
Statement-1 is True, Statement-2 is True, Statement-2 is NOT a correct explantion for Statement-1
Statement-1 is True, Statement-2 is False
Statement-1 is False, Statement-2 is True.
To analyze the statements regarding angular momentum, let's break down the concepts step by step.
Step 1: Understanding Angular Momentum
Angular momentum (L) of a particle is defined as the product of its linear momentum (p) and the perpendicular distance (r) from the point about which it is being measured to the line of action of the momentum. Mathematically, it can be expressed as:
L=r×p
where p=mv (mass times velocity).
Step 2: Evaluating Statement 1
Statement 1: "It is not necessary for a particle to move in a circular path to define angular momentum. It can be defined about any point in space."
This statement is true. Angular momentum can be defined for any particle regardless of its path. Whether the particle is moving in a straight line or a circular path, we can calculate its angular momentum about any point in space.
Step 3: Evaluating Statement 2
Statement 2: "A particle moving in a straight line has non-zero angular momentum about a point which is not lying on the path of the particle."
This statement is also true. If a particle is moving in a straight line and we consider a point not on that line, the perpendicular distance from the point to the line of motion will be non-zero. Therefore, the angular momentum about that point will also be non-zero since:
L=mvr
where r is the perpendicular distance from the point to the line of motion.
Step 4: Conclusion
Both statements are true. However, Statement 2 does not provide an explanation for Statement 1. Thus, the correct conclusion is that both statements are true, but Statement 2 does not explain Statement 1.
Final Answer
Both Statement 1 and Statement 2 are true, but Statement 2 does not explain Statement 1. Therefore, the answer is B.
---
Angular momentum (L) of a particle is defined as the product of its linear momentum (p) and the perpendicular distance (r) from the point about which it is being measured to the line of action of the momentum. Mathematically, it can be expressed as:
L=r×p
where p=mv (mass times velocity).
Statement 1: "It is not necessary for a particle to move in a circular path to define angular momentum. It can be defined about any point in space."
Statement 2: "A particle moving in a straight line has non-zero angular momentum about a point which is not lying on the path of the particle."
L=mvr
where r is the perpendicular distance from the point to the line of motion.
Both statements are true. However, Statement 2 does not provide an explanation for Statement 1. Thus, the correct conclusion is that both statements are true, but Statement 2 does not explain Statement 1.
Both Statement 1 and Statement 2 are true, but Statement 2 does not explain Statement 1. Therefore, the answer is B.
Similar Questions
Select the correct statement. For a particle moving on a straight line
View SolutionA particle moves on a straight line with a uniform velocity. It's angular momentum
View SolutionA particle is moving along a straight line with increasing speed. Its angular momentum about a fixed point on this line :
View SolutionTwo particle A and B are moving as shown in the figure
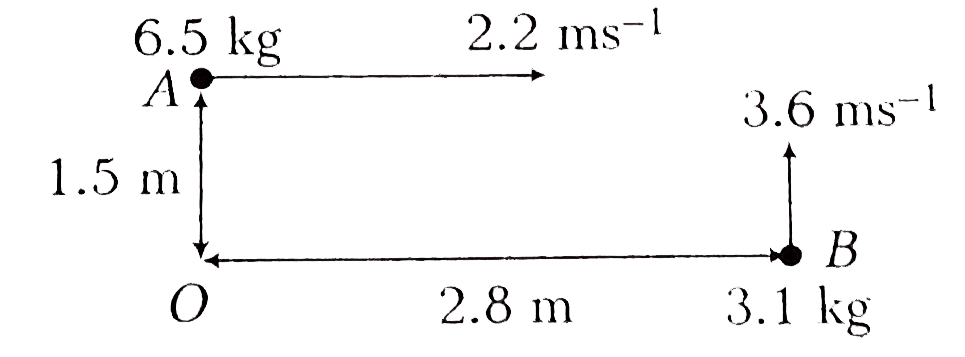
Their total angular momentum about the point O is
View SolutionA particle moving in a circular path has an angular momentum of L. If the frequency of rotation is halved, then its angular momentum becomes
View SolutionAn electron moves round the nucleus of an atom, in a circular path. What is the direction of the angular momentum of the electron ?
View SolutionA particle is moving along a straight line parallel to x-axis with constant velocity. Find angular momentum about the origin in vector form :

View SolutionA particle of mass m is rotating in a plane in circular path of radius r. Its angular momentum is L. The centripetal force acting on the particle is
View SolutionAssertion : If a particle moves with a constant velocity, then angular momentum of this particle about any point remains constant.
Reason : Angular momentum has the units of Plank's constant.
View SolutionA particle moves in a circular path with constant speed .Find out a point about which the angular momentum of the particle is constant and another point about which changes with time.
View Solution
