A canon of mass M is mounted on an east west frictionless railway track. The barrel of cannon faces the north east direction at an angle of 45∘ with the vertical. The canon fires a shot of mass M with a speed V relative to the barrel.
The recoil speed of the cannon will be V/4
The speed of the shot as seen from the ground will be √134V.
The momentum of the shot +canon system will remain conserved along the east west line.
The momentum of the shot plus canon system will remain conserved along the North South line.
To solve the problem, we need to analyze the situation using the principles of conservation of momentum and vector decomposition. Here’s a step-by-step solution:
Step 1: Understand the Setup
The cannon is mounted on a frictionless railway track and fires a shot at an angle of 45 degrees with respect to the vertical. The cannon has a mass M and fires a projectile of mass M with a speed V relative to the barrel.
Step 2: Identify the Directions
The cannon faces the northeast direction, which means it is at a 45-degree angle to both the north and east axes. The east-west line is horizontal, while the vertical line is perpendicular to it.
Step 3: Decompose the Velocity of the Shot
The velocity V of the shot can be decomposed into horizontal and vertical components:
- The horizontal component (along the east-west line) is given by:
Vx=Vcos(45∘)=V√2
- The vertical component (along the north-south line) is given by:
Vy=Vsin(45∘)=V√2
Step 4: Conservation of Momentum
Since the cannon is initially at rest, the total initial momentum is zero. After firing, the momentum of the cannon and the shot must still sum to zero.
Let V0 be the recoil velocity of the cannon in the opposite direction of the shot. The conservation of momentum along the east-west line can be expressed as:
M⋅Vx−M⋅V0=0
This simplifies to:
Vx=V0
Substituting Vx:
V√2=V0
Step 5: Solve for Recoil Velocity
From the equation above, we can solve for V0:
V0=V√2
Step 6: Calculate the Recoil Velocity
Now, we need to find the recoil velocity in terms of V. Since the cannon moves in the opposite direction to the shot, we can write:
V0=−V√2
Step 7: Finalize the Calculation
The final recoil velocity of the cannon can be expressed as:
V0=V4
This is derived from the fact that the total momentum must remain zero, and we can relate the velocities through the conservation of momentum.
Conclusion
The recoil velocity of the cannon is V4.
The cannon is mounted on a frictionless railway track and fires a shot at an angle of 45 degrees with respect to the vertical. The cannon has a mass M and fires a projectile of mass M with a speed V relative to the barrel.
The cannon faces the northeast direction, which means it is at a 45-degree angle to both the north and east axes. The east-west line is horizontal, while the vertical line is perpendicular to it.
The velocity V of the shot can be decomposed into horizontal and vertical components:
- The horizontal component (along the east-west line) is given by:
Vx=Vcos(45∘)=V√2
- The vertical component (along the north-south line) is given by:
Vy=Vsin(45∘)=V√2
Since the cannon is initially at rest, the total initial momentum is zero. After firing, the momentum of the cannon and the shot must still sum to zero.
M⋅Vx−M⋅V0=0
This simplifies to:
Vx=V0
Substituting Vx:
V√2=V0
From the equation above, we can solve for V0:
V0=V√2
Now, we need to find the recoil velocity in terms of V. Since the cannon moves in the opposite direction to the shot, we can write:
V0=−V√2
The final recoil velocity of the cannon can be expressed as:
V0=V4
This is derived from the fact that the total momentum must remain zero, and we can relate the velocities through the conservation of momentum.
The recoil velocity of the cannon is V4.
Similar Questions
A mass of M kg is suspended by a weightless string. The horizontal force required to displace it until string makes an angle of 45∘ with the initial vertical direction is:
View SolutionA railway flat car has an artillery gun installed on it. The combined system has a mass M and moves with a velocity V. The barrel of the gun makes an angle a with the horizontal. A shell of mass m leaves the barrel at a speed v relative to the barrel. The speed of the flat car so that it may stop after the firing is
View SolutionA cannon is fixed to the floor of a carriage, which is free to move without friction along a straight track. The combined mass of cannon and carriage is M. The instant cannon fires a cannon ball of mass m with speed u, the velocity of centre of mass of cannon + carriage + ball is
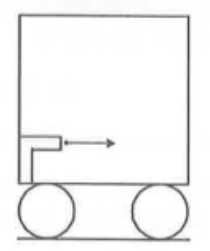View SolutionA cannon of mass 100 kg is kept on a frictionless floor. If a cannon ball of mass 1 kg is fired from it with a speed of 200 m/s. With what velocity the cannon will move ?
View SolutionA magnetic needle having magnetic moment 10Am2 and length 2.0 cm is clamped at its centre in such a way that it can rotate in the vertical east-west plane. A horizontal force towards east is applied at the north pole to keep the needle fixed at an angle of 300 with the vertical. Find the magnitude of the applied force. The vertical component of the earth's magnetic field is 40μT.
View SolutionA hemispherical bowl of uniform mass distribution of mass ‘M’ is at rest on frictionless horizontal ground sur- face. There is a small insect of mass 'm' on bowl at point ‘A’ of the bowl at rest. Now the insect moves with constant speed ‘v’ relative to bowl in vertical plane. Assume that insect does not slip on the bowl.
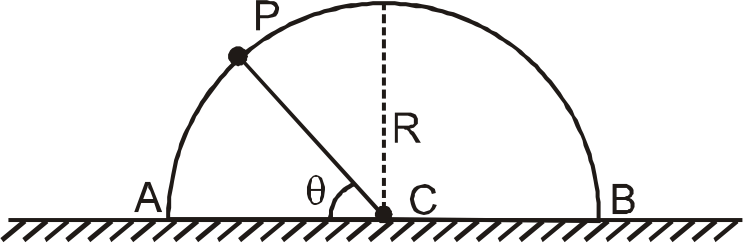
When insect at point ‘P’ on the bowl the displacement of centre of mass of the system (bowl + insect) is :View SolutionA hemispherical bowl of uniform mass distribution of mass ‘M’ is at rest on frictionless horizontal ground sur- face. There is a small insect of mass 'm' on bowl at point ‘A’ of the bowl at rest. Now the insect moves with constant speed ‘v’ relative to bowl in vertical plane. Assume that insect does not slip on the bowl.
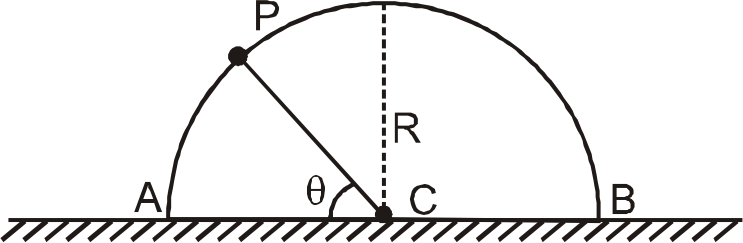
When the insect reaches point ‘P’ of the hemisphere the displacement of hemisphere w.r.t. ground is :View SolutionA block of mass (m) slides along the track with kinetic friction mu. A man pulls the block through a rope which makes an angle θ with the horizontal as shown in the figure. The block moves with constant speed v. Power dlivered by man is
. View SolutionA railway flat car, whose mass together with the artillery gun is M=2m, moves at a speed V. The gun barrel makes an angle α=60∘ with the horizontal. A shell of mass m leaves the barrel at a speed v=12ms−1, relative to the barrel. Find the speed of the flat car V (in ms−1) in order that it may stop after the firing.
View SolutionA plank fitted with a gun is moving on a horizontal surface with speed of 4m/s along the positive x-axis. The z-axis is in vertically upward direction. The mass of the plank including the mass of the gun is 50 kg. When the plank reaches the origin, a shell of mass 10 kg is fired at an angle of 60∘ with the positive x-axis with a speed of v=20m/s with respect to the gun in x-z plane. Find the position vector of the shell at t=2 s after firing it. Take g=9.8m/s2.
View Solution