A hemispherical bowl of uniform mass distribution of mass ‘M’ is at rest on frictionless horizontal ground sur- face. There is a small insect of mass 'm' on bowl at point ‘A’ of the bowl at rest. Now the insect moves with constant speed ‘v’ relative to bowl in vertical plane. Assume that insect does not slip on the bowl.
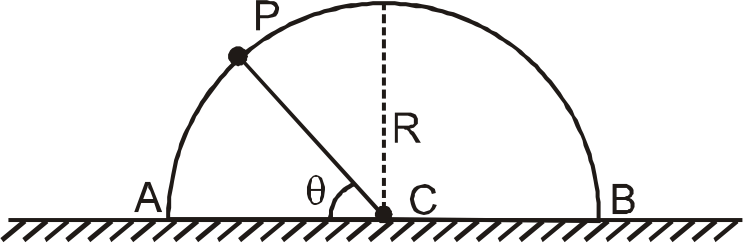
When insect at point ‘P’ on the bowl the displacement of centre of mass of the system (bowl + insect) is :
mRcosθ(M+m) vertically upwards
zero
mRsinθ(M+m) vertically upwrads
MRsinθ(M+m) vertically upwards
NA
Topper's Solved these Questions
Similar Questions
A radioactive element decays by β−emission. A detector records n beta particles in 2s and in next 2s it records 0.75n beta particles. Find mean life correct to nearest whole number. Given ln |2|=0.6931, ln |3|=1.0986.
View SolutionWhen p−n junction diode is forward biased, then
View SolutionA small mass of 10 g lies in a hemispherical bowl of radius 0.5 m at a height of 0.1 m from the bottom of the bowl. The mass will be in equilibrius if the bowl rotates at an
View SolutionA hemispherical bowl of uniform mass distribution of mass ‘M’ is at rest on frictionless horizontal ground sur- face. There is a small insect of mass 'm' on bowl at point ‘A’ of the bowl at rest. Now the insect moves with constant speed ‘v’ relative to bowl in vertical plane. Assume that insect does not slip on the bowl. When the insect reaches point ‘P’ of the hemisphere the displacement of hemisphere w.r.t. ground is :
View SolutionA hemispherical bowl of uniform mass distribution of mass ‘M’ is at rest on frictionless horizontal ground sur- face. There is a small insect of mass 'm' on bowl at point ‘A’ of the bowl at rest. Now the insect moves with constant speed ‘v’ relative to bowl in vertical plane. Assume that insect does not slip on the bowl.

When the insect is at point ‘P’ of the hemispherical bowl the acceleration of bowl is :
View SolutionA hemispherical bowl of uniform mass distribution of mass ‘M’ is at rest on frictionless horizontal ground sur- face. There is a small insect of mass 'm' on bowl at point ‘A’ of the bowl at rest. Now the insect moves with constant speed ‘v’ relative to bowl in vertical plane. Assume that insect does not slip on the bowl.

When insect at point ‘P’ on the bowl the displacement of centre of mass of the system (bowl + insect) is :
View SolutionThe coefficient of friction between a hemispherical bowl and an insect is sqrt(0.44) and the radius of the bowl is 0.6m . The maximum height to which an insect can crawl in the bowl will be .
View SolutionIf the coefficient of friction between an insect and bowl is μ and the radius of the bowl is r, find the maximum height to which the insect can crawl in the bowl.
View SolutionA small insect is climbing slowly along the inner wall of a hemispherical bowl of radius R. The insect is unable to climb beyond theta = 45^(@) . Whenever it tries to climb beyond theta = 45^(@) , it slips. (a) Find the minimum angular speed omega with which the bowl shall be rotated about its vertical radius so that the insect can climb upto theta = 60^(@) . (b) Find minimum omega for which the insect can move out of the bowl.
View SolutionThe coefficient of friction between an insect and a hemispherical bowl of radius r is mu . The maximum height to which the insect can crawl in the bowl is
View SolutionThe coefficient of friction between a hemispherical bowl and an insect is √0.44 and the radius of the bowl is 0.6m. The maximum height to which an insect can crawl in the bowl will be
View SolutionWhat is the work done in upturning a thin hemispherical bowl as shown in the figure. The mass of the bowl is M and the radius of the bowl is R.
View SolutionThe co-efficient of friction between an insect and bowl is ul and the radius of the bowl is r. The maximum height to which the insect can crawl in the bowl is
View SolutionA mass .m. is released, with a horizontal speed v from the top of a smooth and fixed, hemispherical bowl, of radius r. The angle theta w.r.t. the vertical where it leaves constant with the bowl is
View SolutionIf the coefficient of friction between an insect and bowl is μ and the radius of the bowl is r, find the maximum height to which the insect can crawl in the bowl.
View Solution
