A rod of mass m and length l suspended from a point swings in a vertica plane such that magnitude of acceleration of its C.M. at extreme points is same as that at the mean point then :
The deflectin angle from the vertical to the extreme position is cos−1(3/5)
At the extreme position there is no centripetal acceleration of the CM.
At the mean position there is no tangential acceleration of the CM.
The angular momentum of the rod about the suspension point remains constant
To solve the problem, we need to analyze the motion of a rod of mass m and length l that swings in a vertical plane. We are given that the magnitude of the acceleration of its center of mass (C.M.) at the extreme points is the same as that at the mean point.
1. Understanding the Setup:
- The rod is suspended from a pivot point and swings in a vertical plane.
- The extreme positions are the highest points in the swing, and the mean position is the lowest point.
2. Acceleration at the Mean Position:
- At the mean position, the rod has maximum velocity, and the centripetal acceleration is present.
- The centripetal acceleration ac at the mean position is given by:
ac=V2L
- Here, V is the velocity at the mean position, and L is the length of the rod.
3. Acceleration at the Extreme Position:
- At the extreme position, the velocity of the rod is zero, thus the centripetal acceleration is also zero.
- The tangential acceleration at at the extreme position can be calculated using gravitational force components. The tangential acceleration is given by:
at=gsin(θ)
- Here, θ is the angle from the vertical.
4. Equating Accelerations:
- According to the problem, the magnitude of the acceleration of the center of mass at the extreme points is the same as that at the mean point:
gsin(θ)=V2L
5. Using Energy Conservation:
- We can apply the conservation of mechanical energy between the extreme position and the mean position.
- At the extreme position, the potential energy is maximum, and kinetic energy is zero:
PEextreme=mgh=mg(L−Lcos(θ))=mgL(1−cos(θ))
- At the mean position, the potential energy is zero, and all energy is kinetic:
KEmean=12mV2
- Setting these equal gives:
mgL(1−cos(θ))=12mV2
- Canceling m and rearranging gives:
V2=2gL(1−cos(θ))
6. Substituting for V2:
- Substitute V2 back into the acceleration equation:
gsin(θ)=2gL(1−cos(θ))L
- Simplifying gives:
gsin(θ)=2g(1−cos(θ))
- Canceling g (assuming g≠0):
sin(θ)=2(1−cos(θ))
7. Using Trigonometric Identity:
- We can use the identity sin2(θ)+cos2(θ)=1:
sin(θ)=2(1−cos(θ))
- Squaring both sides gives:
sin2(θ)=4(1−cos(θ))2
- Expanding and substituting sin2(θ):
1−cos2(θ)=4(1−2cos(θ)+cos2(θ))
- Rearranging leads to a quadratic equation in cos(θ).
8. Solving the Quadratic Equation:
- After simplification, we find:
5cos2(θ)−8cos(θ)+3=0
- Solving this quadratic gives us the possible values for cos(θ).
9. Finding θ:
- The solutions yield cos(θ)=35 or cos(θ)=1.
- The angle θ at the extreme position is:
θ=cos−1(35)
Final Result:
The deflection angle from the vertical to the extreme position is θ=cos−1(35).
- The rod is suspended from a pivot point and swings in a vertical plane.
- The extreme positions are the highest points in the swing, and the mean position is the lowest point.
- At the mean position, the rod has maximum velocity, and the centripetal acceleration is present.
- The centripetal acceleration ac at the mean position is given by:
ac=V2L
- Here, V is the velocity at the mean position, and L is the length of the rod.
- At the extreme position, the velocity of the rod is zero, thus the centripetal acceleration is also zero.
- The tangential acceleration at at the extreme position can be calculated using gravitational force components. The tangential acceleration is given by:
at=gsin(θ)
- Here, θ is the angle from the vertical.
- According to the problem, the magnitude of the acceleration of the center of mass at the extreme points is the same as that at the mean point:
gsin(θ)=V2L
- We can apply the conservation of mechanical energy between the extreme position and the mean position.
- At the extreme position, the potential energy is maximum, and kinetic energy is zero:
PEextreme=mgh=mg(L−Lcos(θ))=mgL(1−cos(θ))
- At the mean position, the potential energy is zero, and all energy is kinetic:
KEmean=12mV2
- Setting these equal gives:
mgL(1−cos(θ))=12mV2
- Canceling m and rearranging gives:
V2=2gL(1−cos(θ))
- Substitute V2 back into the acceleration equation:
gsin(θ)=2gL(1−cos(θ))L
- Simplifying gives:
gsin(θ)=2g(1−cos(θ))
- Canceling g (assuming g≠0):
sin(θ)=2(1−cos(θ))
- We can use the identity sin2(θ)+cos2(θ)=1:
sin(θ)=2(1−cos(θ))
- Squaring both sides gives:
sin2(θ)=4(1−cos(θ))2
- Expanding and substituting sin2(θ):
1−cos2(θ)=4(1−2cos(θ)+cos2(θ))
- Rearranging leads to a quadratic equation in cos(θ).
- After simplification, we find:
5cos2(θ)−8cos(θ)+3=0
- Solving this quadratic gives us the possible values for cos(θ).
- The solutions yield cos(θ)=35 or cos(θ)=1.
- The angle θ at the extreme position is:
θ=cos−1(35)
The deflection angle from the vertical to the extreme position is θ=cos−1(35).
Similar Questions
A ball attached to one end of a string swings in a vertical plane such that its acceleration at point A (extreme position) is equal to its acceleration at point B (mean position), The angle θ is
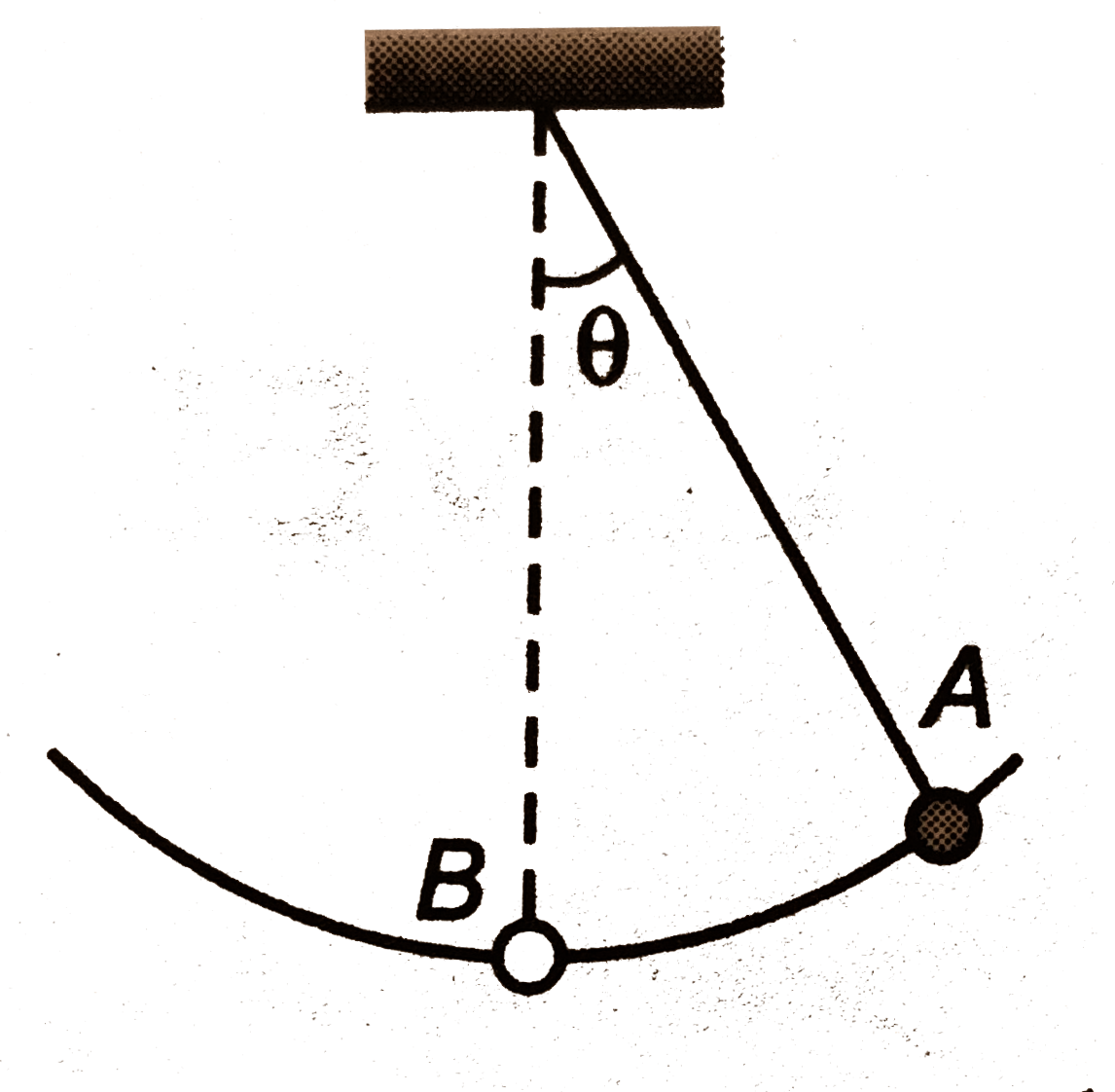
View Solution(a) A ball, suspended by a thread, swings in a vertical plane so that its acceleration in the extreme and the lowest positions are equal. The angle θ of thread deflection in the extreme position will be
( b) The kinetic energy of a particle moving in a circle of radius R depens on the distance covered as T=as2 , where 'a' is a constant. Find the force acting on the particle as a function of s.
View SolutionA ball suspended by a thread swing in a vertical plane that its acceleration values in the lowest possition and the extreme postition are equal . Find the thread deffection angle in the extreme possition.
View SolutionA uniform rod of mass m and length l is suspended about its end. Time period of small angular oscillations is

View SolutionA uniform rod of mass 20 Kg and length 1.6 m is piovted at its end and swings freely in the vertical plane. Angular acceleration of the rod just after the rod is relased from rest in the horizontal position is

View SolutionA uniform rod of mass m and length l can rotate in a vertical plane about a smooth horizontal axis point H. a. Find angular acceleration α of the rod. just after it is released from initial horizontal position from rest'? b. Calculate the acceleration (tangential and radial) , point A at this moment.
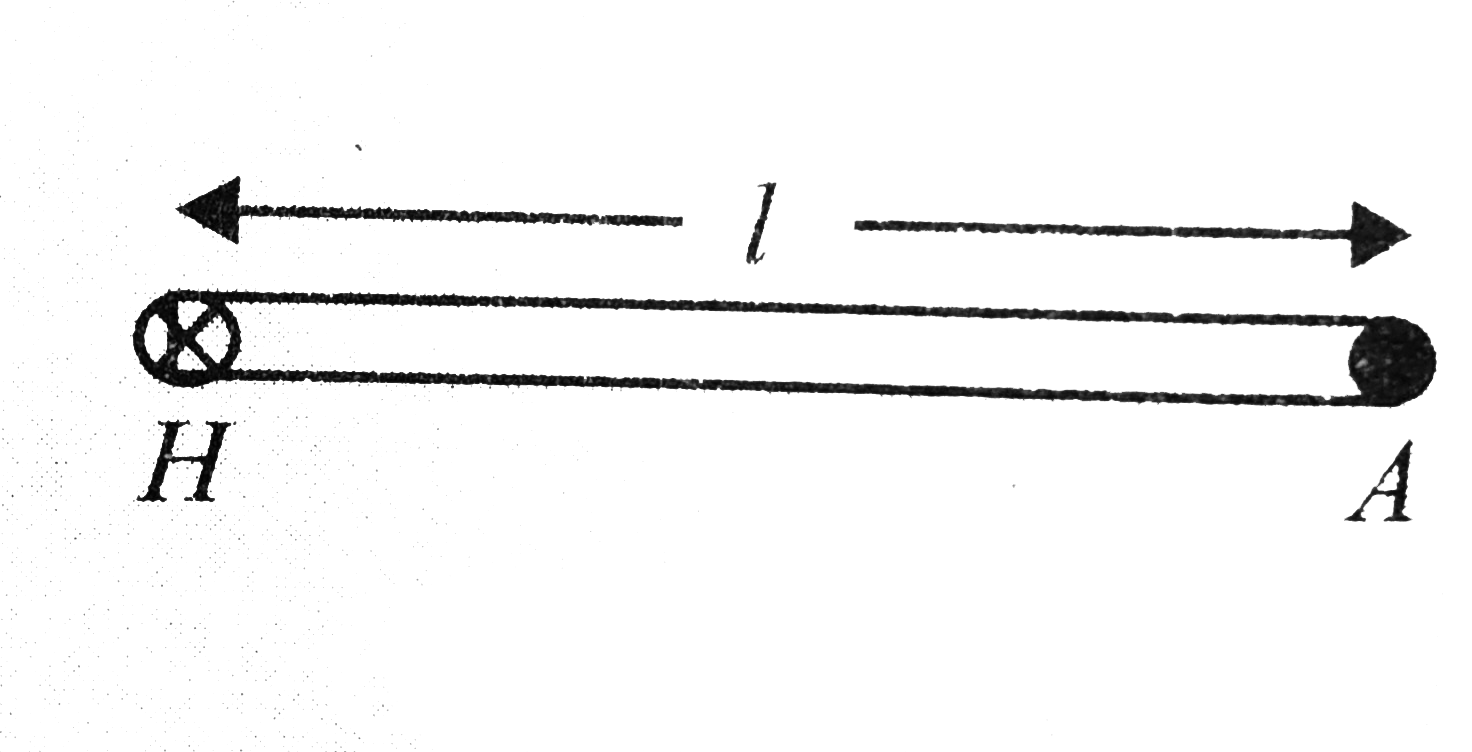
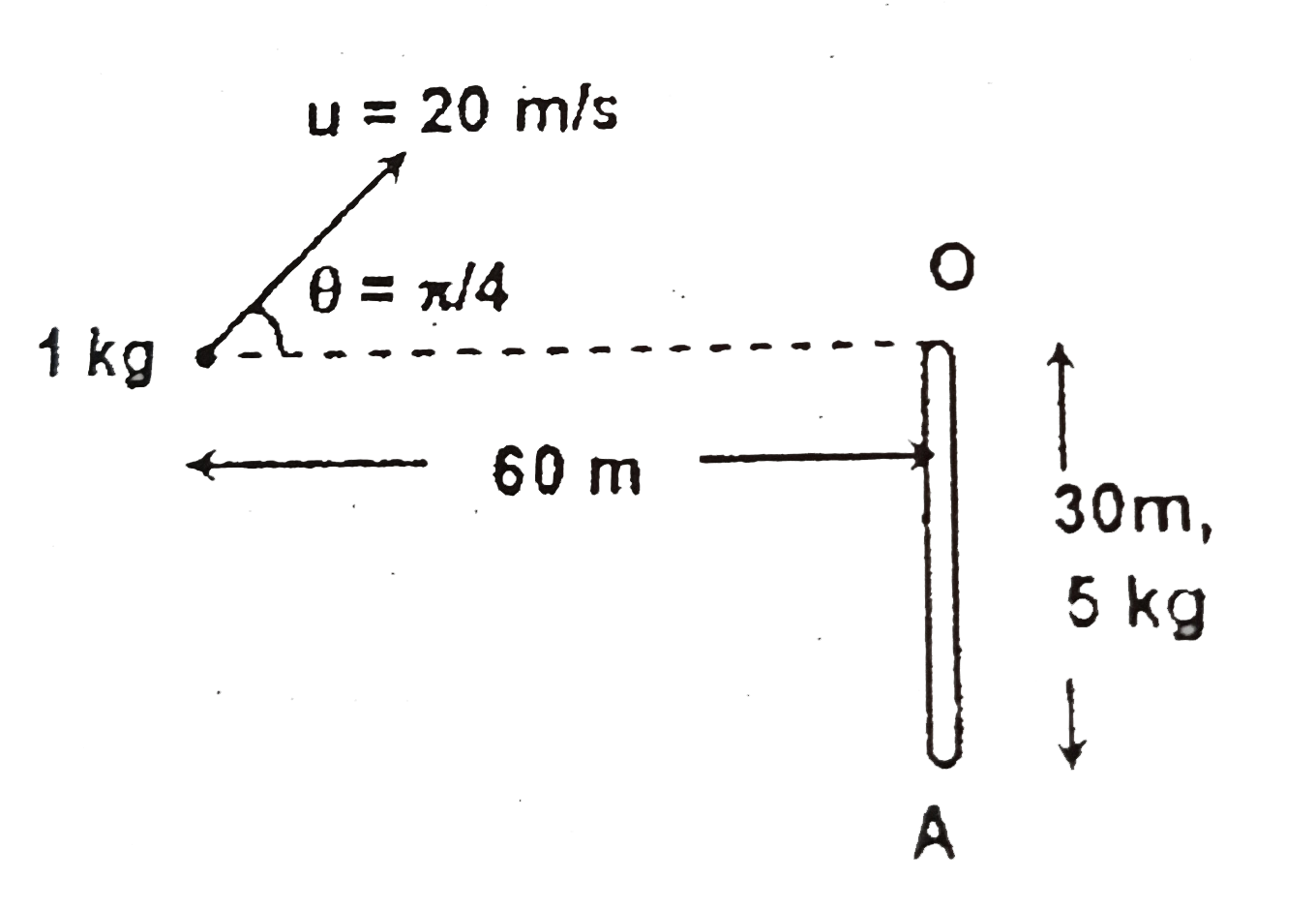
View SolutionA particle of mass 1kg is projected at an angle of θ=π/4 from horizontal with a muzzle velocity of 20m/s. A long slender rod of mass 5kg and length 30m is suspended vertically from a point at the same horizontal leves as that of point of projection and at a distance of 60m from the projection point. The rod can rotate freely. If collision occurs, it is perfectly plastic. (g=10m/s2)
If the rod tilts to an angle θ after collision, then
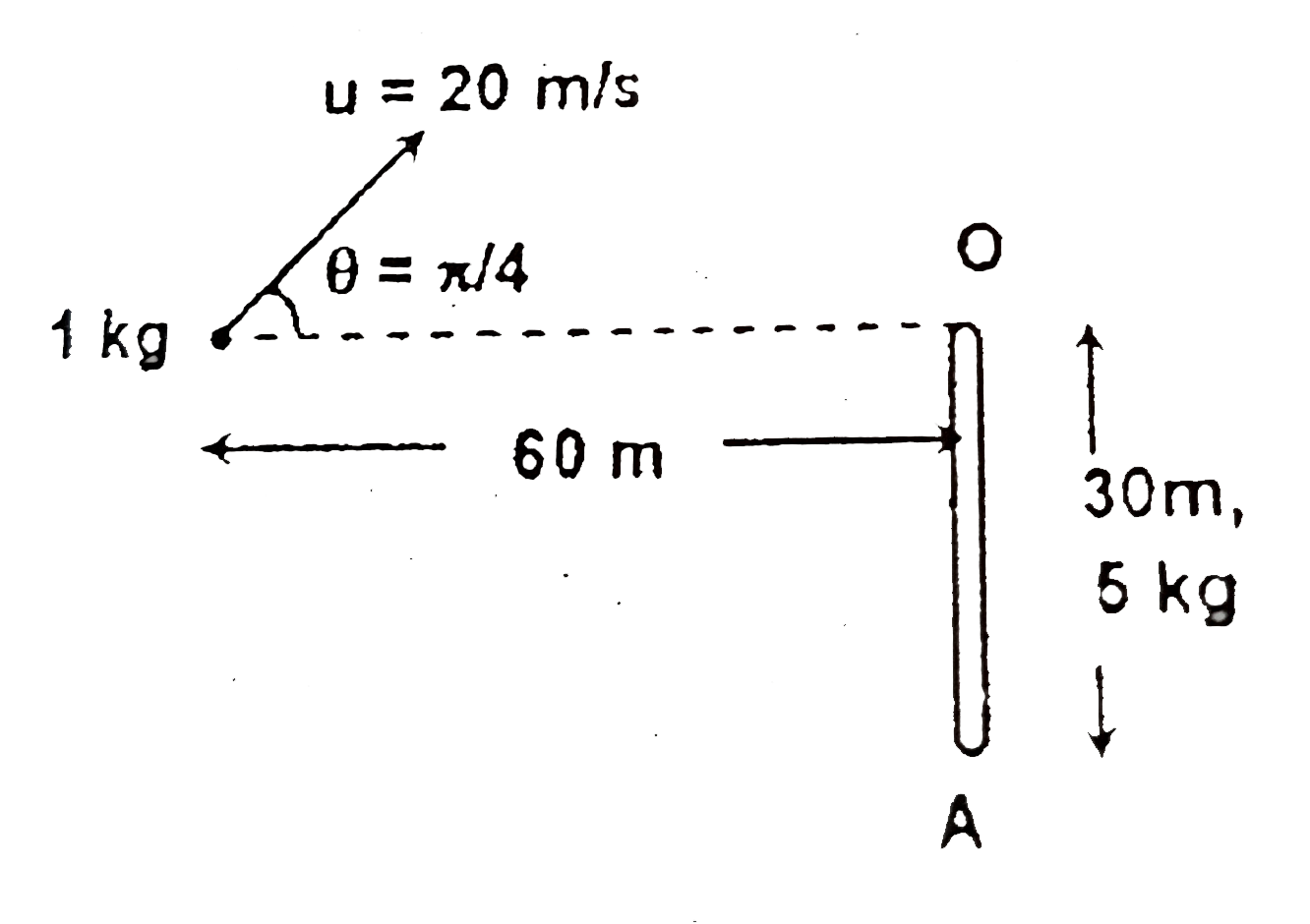
View SolutionA particle of mass 1kg is projected at an angle of θ=π/4 from horizontal with a muzzle velocity of 20m/s. A long slender rod of mass 5kg and length 30m is suspended vertically from a point at the same horizontal leves as that of point of projection and at a distance of 60m from the projection point. The rod can rotate freely. If collision occurs, it is perfectly plastic. (g=10m/s2)
Angular velocity of rod after collision is
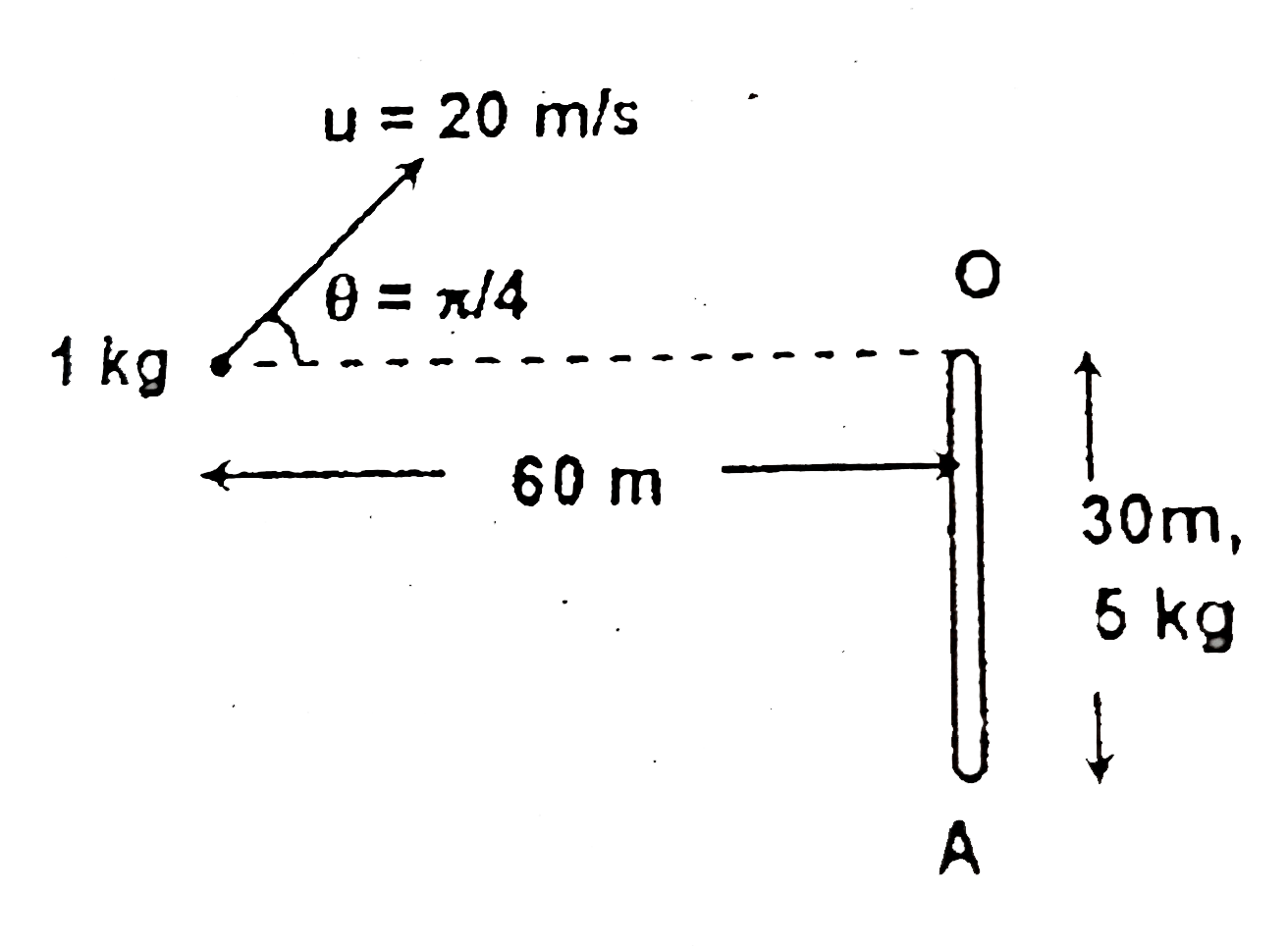
View SolutionA particle of mass 1kg is projected at an angle of θ=π/4 from horizontal with a muzzle velocity of 20m/s. A long slender rod of mass 5kg and length 30m is suspended vertically from a point at the same horizontal leves as that of point of projection and at a distance of 60m from the projection point. The rod can rotate freely. If collision occurs, it is perfectly plastic. (g=10m/s2)
If projectile is fired horizontally, it will
View SolutionA thin rod of mass m and length l is suspended from one of its ends. It is set into oscillation about a horizontal axis. Its angular speed is ω while passing through its mean position. How high will its centre of mass rise from its lowest position ?
View Solution
