(a) A ball, suspended by a thread, swings in a vertical plane so that its acceleration in the extreme and the lowest positions are equal. The angle θ of thread deflection in the extreme position will be
( b) The kinetic energy of a particle moving in a circle of radius R depens on the distance covered as T=as2 , where 'a' is a constant. Find the force acting on the particle as a function of s.
tan−1(2)
tan−1(√2)
tan−1(12)
2tan−1(12)
The correct Answer is:D
Step by step video & image solution for (a) A ball, suspended by a thread, swings in a vertical plane so that its acceleration in the extreme and the lowest positions are equal. The angle θ of thread deflection in the extreme position will be ( b) The kinetic energy of a particle moving in a circle of radius R depens on the distance covered as T = as^(2) , where 'a' is a constant. Find the force acting on the particle as a function of s. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - JEE Advanced
24 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - More than One Option is Correct
13 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Subjective Questions
2 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct
27 Videos
Similar Questions
(a) A ball, suspended by a thread, swings in a vertical plane so that its acceleration in the extreme and the lowest positions are equal. The angle θ of thread deflection in the extreme position will be
( b) The kinetic energy of a particle moving in a circle of radius R depens on the distance covered as T=as2 , where 'a' is a constant. Find the force acting on the particle as a function of s.
View SolutionThe kinetic energy of a particle moving along a circle of radius R depends on the distance covered s as K.E = KS2 where K is a constant. Find the force acting on the particle as a function of S -
View Solution
Knowledge Check
In simple harmonic motion, at the extreme positions
Akinetic energy is minimum, potential energy is maximumBkinetic energy is maximum, potential energy is minimumCboth kinetic and potential energies are maximum.Dboth kinetic and potential energies are minimum
The kinetic energy of a particle moving along a circle of radius R depends on the distance covered S as K =α.S2, where α is a constant. Find the force acting on the particle as a function of S.
View SolutionA ball suspended by a thread swing in a vertical plane that its acceleration values in the lowest possition and the extreme postition are equal . Find the thread deffection angle in the extreme possition.
View SolutionThe kinetic energy K of a particle moving along a circle of radius R depends upon the distance S as K=βS2 , where β is a constant. Tangential acceleration of the particle is proportional to
View SolutionThe kinetic energy K of a particle moving along a circle of radius R depends upon the distance s as K=as2. The force acting on the particle is
View SolutionThe speed of a particle moving in a circle of radius r=2m varies with time t as v=t2, where t is in second and v in m/s. Find the radial, tangential and net acceleration at t=2s.
View SolutionA ball attached to one end of a string swings in a vertical plane such that its acceleration at point A (extreme position) is equal to its acceleration at point B (mean position), The angle θ is
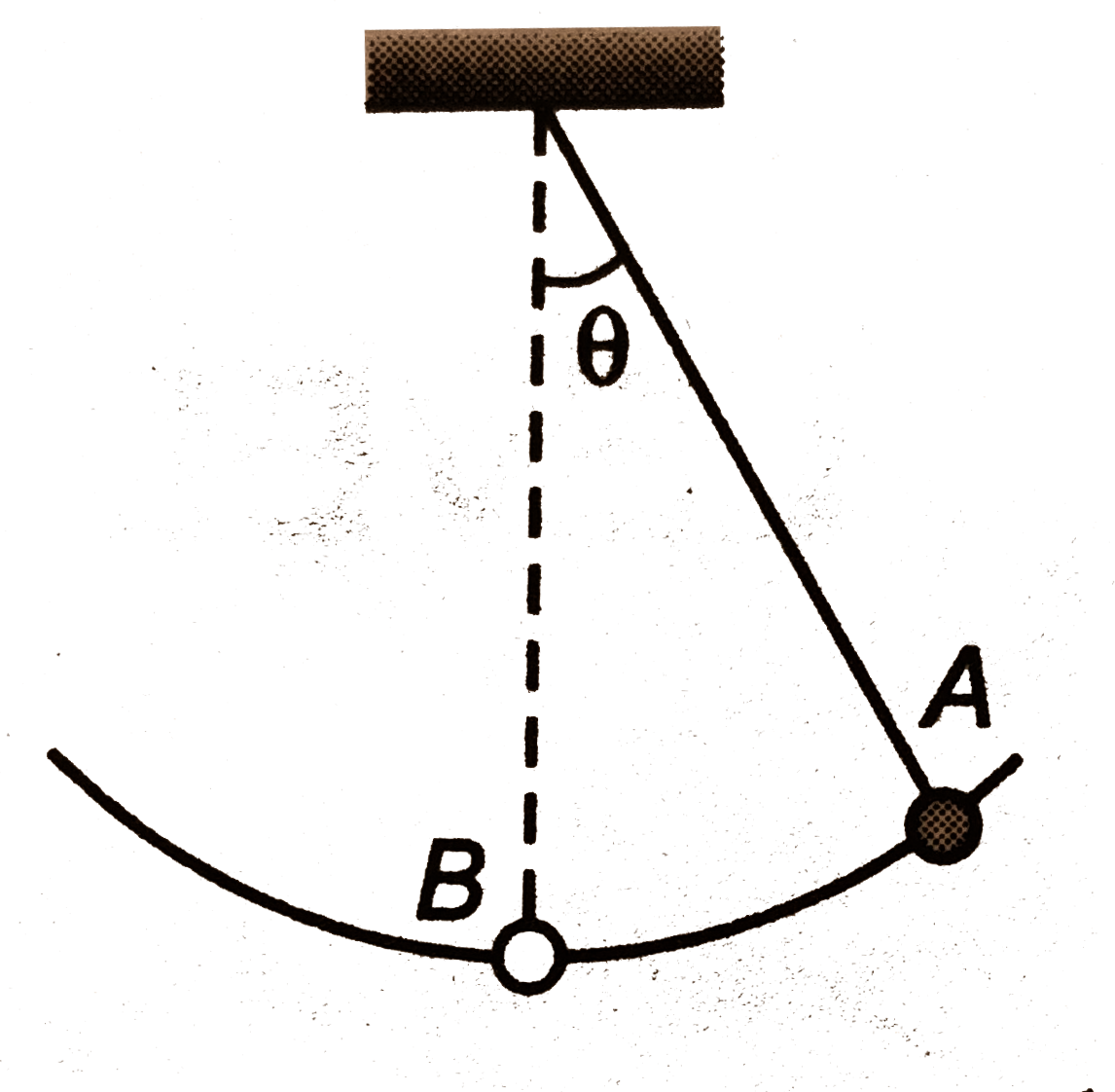
View SolutionA rod of mass m and length l suspended from a point swings in a vertica plane such that magnitude of acceleration of its C.M. at extreme points is same as that at the mean point then :
View Solution
