A ball suspended by a thread swing in a vertical plane that its acceleration values in the lowest possition and the extreme postition are equal . Find the thread deffection angle in the extreme possition.
2tan−112
tan−112
tan−1√2
tan−12
The correct Answer is:A
To solve the problem of finding the deflection angle θ in the extreme position of a ball suspended by a thread swinging in a vertical plane, we can follow these steps:
Step 1: Understand the System
The ball is suspended by a thread of length l and swings in a vertical plane. At the lowest point of the swing, the ball has maximum speed, and at the extreme position, it has maximum height and minimum speed.
Step 2: Identify the Forces and Accelerations
At the lowest point, the centripetal acceleration ac is given by:
ac=v2l
where v is the speed of the ball at the lowest point.
At the extreme position, the tangential acceleration at is given by:
at=gsinθ
where g is the acceleration due to gravity and θ is the angle of deflection from the vertical.
Step 3: Set Up the Equation
According to the problem, the acceleration values at the lowest position and the extreme position are equal:
v2l=gsinθ
Step 4: Use Conservation of Energy
The potential energy at the extreme position is converted into kinetic energy at the lowest point. The height h of the ball at the extreme position can be expressed as:
h=l−lcosθ=l(1−cosθ)
The potential energy at the extreme position is:
PE=mgh=mg(l(1−cosθ))
The kinetic energy at the lowest point is:
KE=12mv2
By conservation of energy:
mg(l(1−cosθ))=12mv2
Step 5: Simplify the Energy Equation
We can cancel m from both sides:
g(l(1−cosθ))=12v2
From the previous centripetal acceleration equation, we have v2=glsinθ. Substituting this into the energy equation gives:
g(l(1−cosθ))=12glsinθ
Dividing both sides by gl (assuming g and l are not zero):
1−cosθ=12sinθ
Step 6: Rearranging the Equation
Rearranging gives:
2(1−cosθ)=sinθ
or
2−2cosθ=sinθ
Step 7: Use Trigonometric Identity
Using the identity sinθ=2sinθ2cosθ2 and 1−cosθ=2sin2θ2:
2−4sin2θ2=2sinθ2cosθ2
Dividing by 2:
1−2sin2θ2=sinθ2cosθ2
Step 8: Solve for θ
This leads us to:
1−2sin2θ2=12sinθ
After some algebra, we find:
1−cosθsinθ=12
This simplifies to:
θ=2tan−1(12)
Final Answer
Thus, the deflection angle θ in the extreme position is:
θ=2tan−1(12)
The ball is suspended by a thread of length l and swings in a vertical plane. At the lowest point of the swing, the ball has maximum speed, and at the extreme position, it has maximum height and minimum speed.
At the lowest point, the centripetal acceleration ac is given by:
ac=v2l
where v is the speed of the ball at the lowest point.
at=gsinθ
where g is the acceleration due to gravity and θ is the angle of deflection from the vertical.
According to the problem, the acceleration values at the lowest position and the extreme position are equal:
v2l=gsinθ
The potential energy at the extreme position is converted into kinetic energy at the lowest point. The height h of the ball at the extreme position can be expressed as:
h=l−lcosθ=l(1−cosθ)
The potential energy at the extreme position is:
PE=mgh=mg(l(1−cosθ))
The kinetic energy at the lowest point is:
KE=12mv2
By conservation of energy:
mg(l(1−cosθ))=12mv2
We can cancel m from both sides:
g(l(1−cosθ))=12v2
From the previous centripetal acceleration equation, we have v2=glsinθ. Substituting this into the energy equation gives:
g(l(1−cosθ))=12glsinθ
Dividing both sides by gl (assuming g and l are not zero):
1−cosθ=12sinθ
Rearranging gives:
2(1−cosθ)=sinθ
or
2−2cosθ=sinθ
Using the identity sinθ=2sinθ2cosθ2 and 1−cosθ=2sin2θ2:
2−4sin2θ2=2sinθ2cosθ2
Dividing by 2:
1−2sin2θ2=sinθ2cosθ2
This leads us to:
1−2sin2θ2=12sinθ
After some algebra, we find:
1−cosθsinθ=12
This simplifies to:
θ=2tan−1(12)
Thus, the deflection angle θ in the extreme position is:
θ=2tan−1(12)
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - DPP 457videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 466videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 4311videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise53videos
CURRENT ELECTRICITY
- BOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems9videos
ELASTICITY AND VISCOCITY
Similar Questions
(a) A ball, suspended by a thread, swings in a vertical plane so that its acceleration in the extreme and the lowest positions are equal. The angle θ of thread deflection in the extreme position will be
( b) The kinetic energy of a particle moving in a circle of radius R depens on the distance covered as T=as2 , where 'a' is a constant. Find the force acting on the particle as a function of s.View Solution(a) A ball, suspended by a thread, swings in a vertical plane so that its acceleration in the extreme and the lowest positions are equal. The angle θ of thread deflection in the extreme position will be
( b) The kinetic energy of a particle moving in a circle of radius R depens on the distance covered as T=as2 , where 'a' is a constant. Find the force acting on the particle as a function of s.View SolutionA ball attached to one end of a string swings in a vertical plane such that its acceleration at point A (extreme position) is equal to its acceleration at point B (mean position), The angle θ is
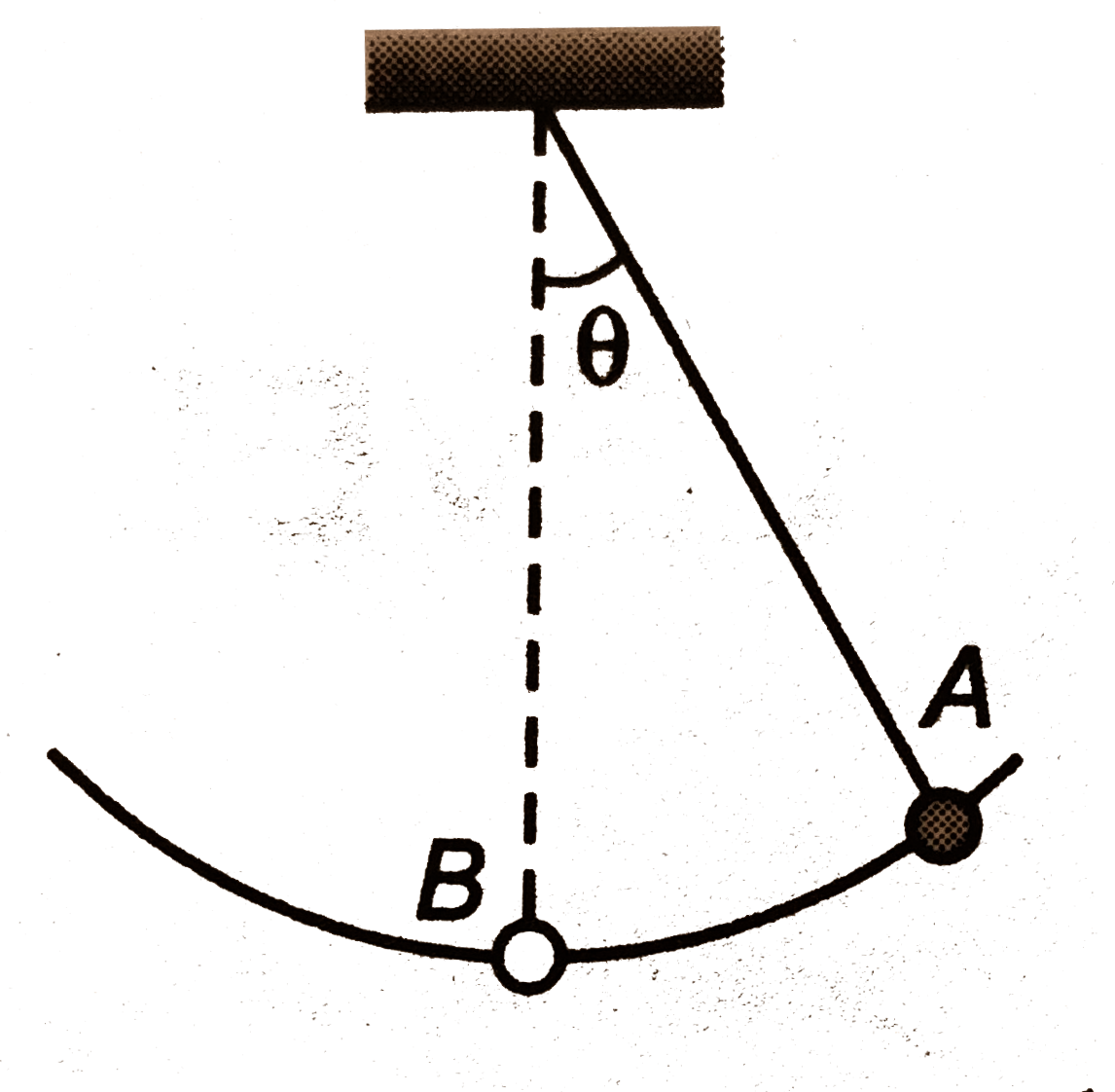 View Solution
View SolutionA rod of mass m and length l suspended from a point swings in a vertica plane such that magnitude of acceleration of its C.M. at extreme points is same as that at the mean point then :
View SolutionA ball is suspended by a thread of length l at the point O on an incline wall as shown. The inclination of the wall with the vertical is (a)the thread is displacement througha small angle away from the vertical and (b) the ball is released. Find the period of obcillation of pendulum. Consider both cases
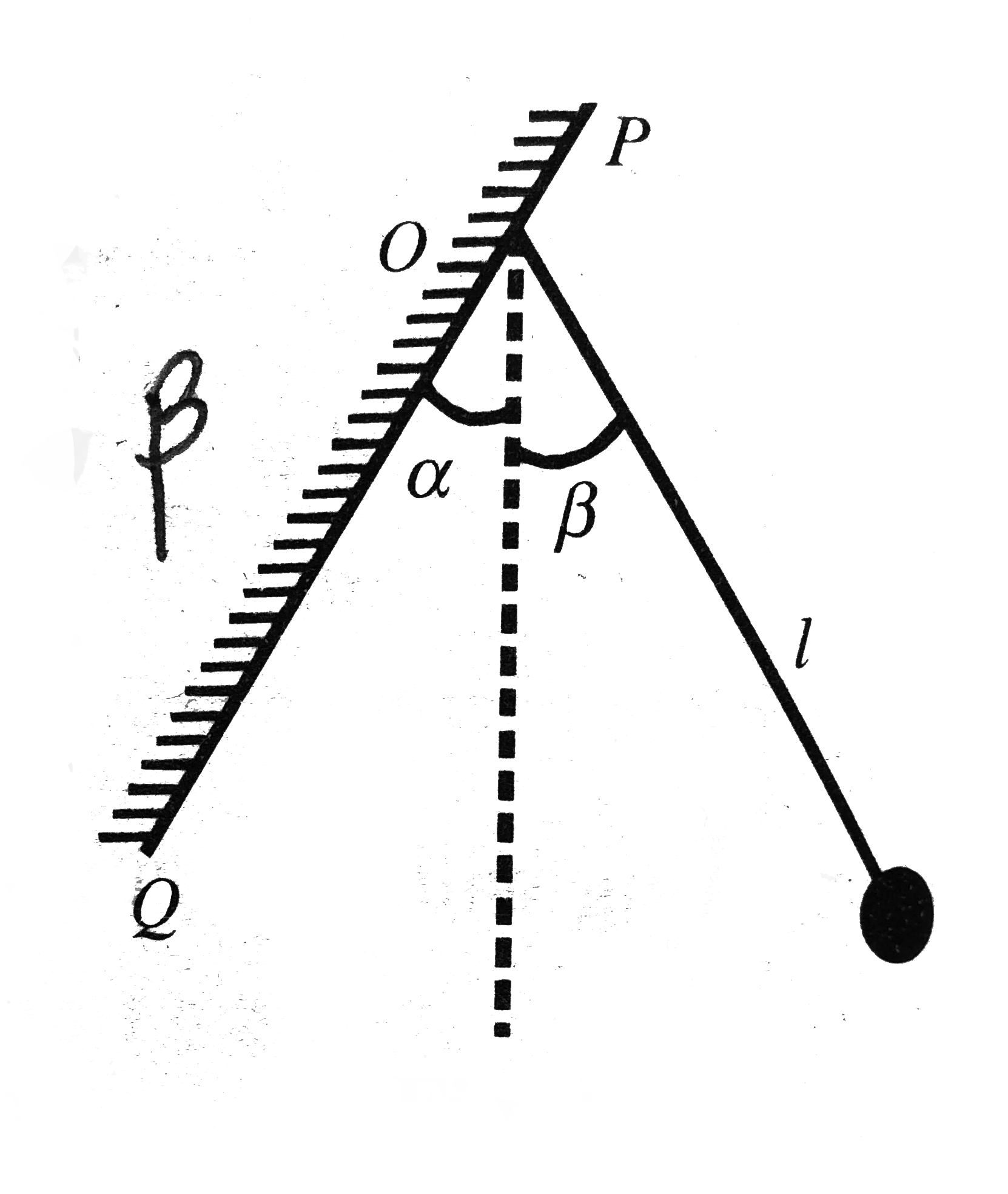
a. α>β
b. α<β
Assuming that any impact between the wall and the ball is elastic.View SolutionA particle tide to the end of a string oscillates along a circular arc in a vertical plane. The other end of the string is fixed at the center of the circle. If the string has a breaking strength of twice the weight of the particles,
a. find the maximum distance that the particle can cover in one cycle of oscillation. The length of the string is 50cm.
b. Find the tension in the extreme position.
c. Find the acceleration of the particle at bottom and extreme position.View SolutionA measurement of the horizatal component B_(H) of the Earth's field at the location of Tuscon, Arizona, gave a value of 26μT . By suspending a small magent like a compass that is free to swing in a vertical plante ,it is possible to measure the angle between the field direction and the horizontal plane, called the inclination or the dip angle ϕ .The dip angle at Tucson was measured to be 60∘ . Find teh magnitude at taht location .
View SolutionA ball is suspended by a thread of length l at the point O on an incline wall as shown. The inclination of the wall with the vertical is α.The thread is displaced through a small angle β away from the vertical and the ball is released. Find the period of oscillation of pendulum.
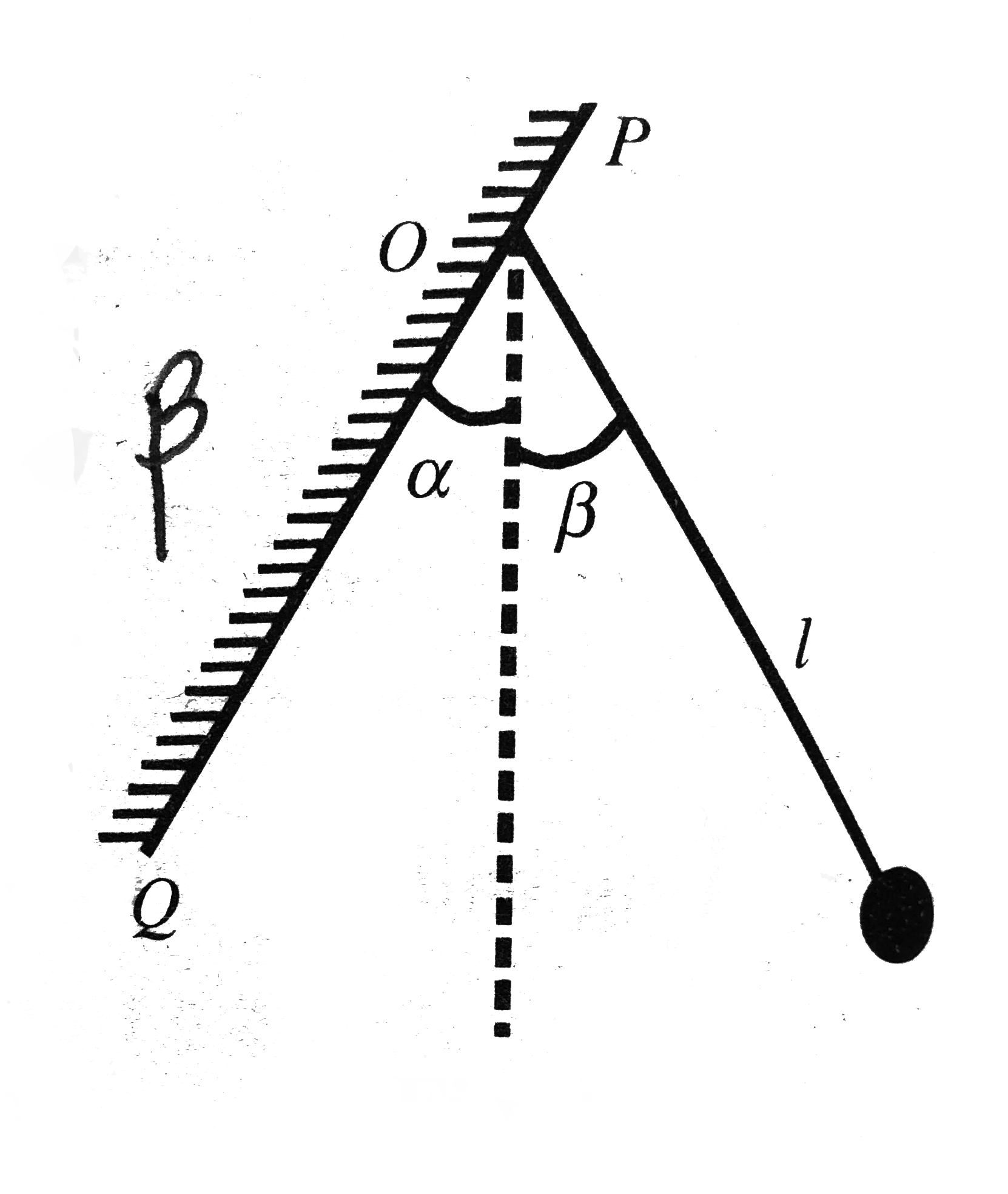
Consider both cases
a. α>β
b. α<β
Assuming that any impact between the wall and the ball is elastic.View SolutionThe bob of a 0.2 m pendulum describs an arc of circle in a vertical plane. If the tension in the cord is √3 times the weight of the bob when the cord makes an angle 30∘ with the vertical, the acceleration of the bob in that position is g/n. Find value of n.
View SolutionA uniform rod of mass m=1.5kg suspended by two identical threads l=90cm in length ( figure ) was turned through a small angle about the vertical axis passing through its middle point C. The threads deviated in the process through an angle α=5.0∘. Then the rod was released to start performing small oscillations.
Find:
(a) the oscillation period.
 View Solution
View Solution

