A sailor in a boat, which is going due east with a speed of 8m/s observes that a submarine is heading towards north at a speed of 12m/s and sinking at a rate of 2m/s.The commander of submarine observes a helicopter ascending at a rate of 5m/s and heading towards west with 4m/s.Find the speed of the helicopter with respect to boat.
To find the speed of the helicopter with respect to the boat, we will break down the problem into manageable steps.
Step 1: Define the Directions
We will define our coordinate system:
- East direction as ^i
- North direction as ^j
- Upward direction as ^k
Step 2: Determine the Velocity of the Submarine
The submarine is moving:
- North at 12m/s (positive ^j direction)
- Sinking down at 2m/s (negative ^k direction)
Thus, the velocity of the submarine with respect to water is:
→Vsub=0^i+12^j−2^k=12^j−2^km/s
Step 3: Determine the Velocity of the Helicopter with Respect to the Submarine
The helicopter is moving:
- West at 4m/s (negative ^i direction)
- Ascending at 5m/s (positive ^k direction)
Thus, the velocity of the helicopter with respect to the submarine is:
→Vhel=−4^i+0^j+5^k=−4^i+5^km/s
Step 4: Calculate the Velocity of the Helicopter with Respect to the Boat
Using the formula:
→Vhel, boat=→Vhel, sub+→Vsub, boat
Substituting the values we found:
→Vhel, boat=(−4^i+5^k)+(0^i+12^j−2^k)
Combining the components:
→Vhel, boat=(−4^i+0^j+5^k)+(0^i+12^j−2^k)=−4^i+12^j+3^km/s
Step 5: Calculate the Speed of the Helicopter with Respect to the Boat
The speed is the magnitude of the velocity vector:
Speed=|→Vhel, boat|=√(−4)2+(12)2+(3)2
Calculating:
=√16+144+9=√169=13m/s
Thus, the speed of the helicopter with respect to the boat is 13 m/s.
We will define our coordinate system:
- East direction as ^i
- North direction as ^j
- Upward direction as ^k
The submarine is moving:
- North at 12m/s (positive ^j direction)
- Sinking down at 2m/s (negative ^k direction)
→Vsub=0^i+12^j−2^k=12^j−2^km/s
The helicopter is moving:
- West at 4m/s (negative ^i direction)
- Ascending at 5m/s (positive ^k direction)
→Vhel=−4^i+0^j+5^k=−4^i+5^km/s
Using the formula:
→Vhel, boat=→Vhel, sub+→Vsub, boat
Substituting the values we found:
→Vhel, boat=(−4^i+5^k)+(0^i+12^j−2^k)
Combining the components:
→Vhel, boat=(−4^i+0^j+5^k)+(0^i+12^j−2^k)=−4^i+12^j+3^km/s
The speed is the magnitude of the velocity vector:
Speed=|→Vhel, boat|=√(−4)2+(12)2+(3)2
Calculating:
=√16+144+9=√169=13m/s
Topper's Solved these Questions
Similar Questions
Find average speed of 40m/s and 50m/s.
View SolutionA car is going in south with a speed of 5m/s. To a man sitting in car a bus appears to move towards west with a speed of 2√6m/s. What is the actual speed of the bus?
View SolutionA ship is sailing towards the north at a speed of 1.25 m/s. The current is taking it towards the east at the rate of 1 m/s and a sailor is climbing a vertical pole on the ship at the rate of 0.5 m/s. Find the velocity of the sailor in space.
View SolutionA ship is sailing towards the north at a speed of 1.25 m/s. The current is taking it towards the east at the rate of 1 m/s and a sailor is climbing a vertical pole on the ship at the rate of 0.5 m/s. Find the velocity of the sailor in space.
View SolutionA man runs towards a mirror at a speed 15 m/s. The speed of the image relative to the man is
View SolutionRam moves in east direction at a speed of 6 m/s and Shyam moves 30∘ east of north at a speed of 6 m/s. The magnitude of their relative velocity is
View SolutionA highly elastic ball moving at a speed of 3m/s approaches a wall moving towards it with a speed of 3m/s. After the collision. the speed of the ball will be
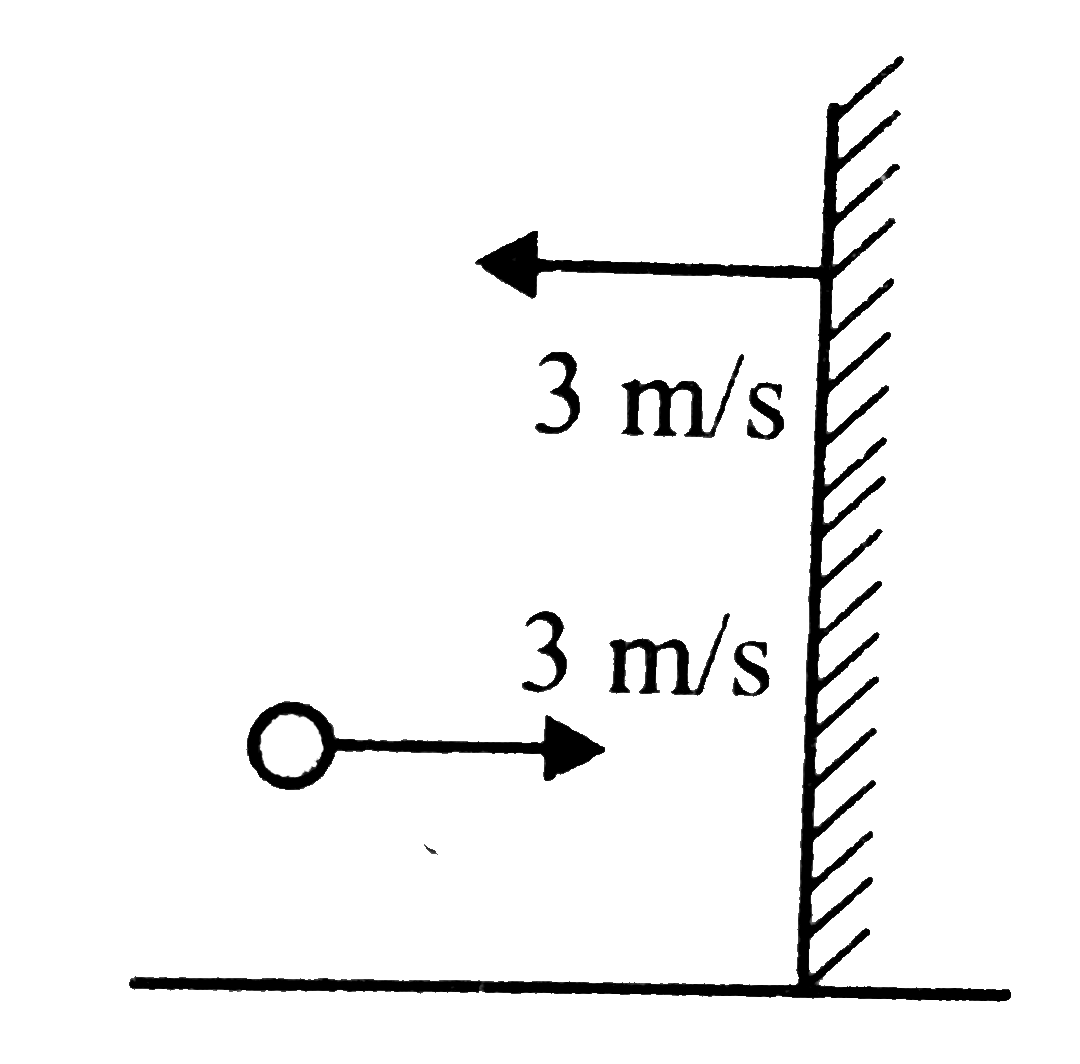 View Solution
View SolutionA ship is steaming towards east with a speed of 8 m/s. A women runs across the deck at a speed of 6ms−1 towards north. What is the velocity of the women relative to the sea ?
View SolutionA vehicle is moving at a speed of 30 m/s on a circular road of radius 450 m. Its speed is increasing at a rate of 2ms2 . The acceleration of particle at this instant is
View SolutionA car is moving at a speed of 40 m/s on a circular track of radius 400 m. this speed is increasing at the rate of 3 m/s2. The acceleration of car is
View Solution

