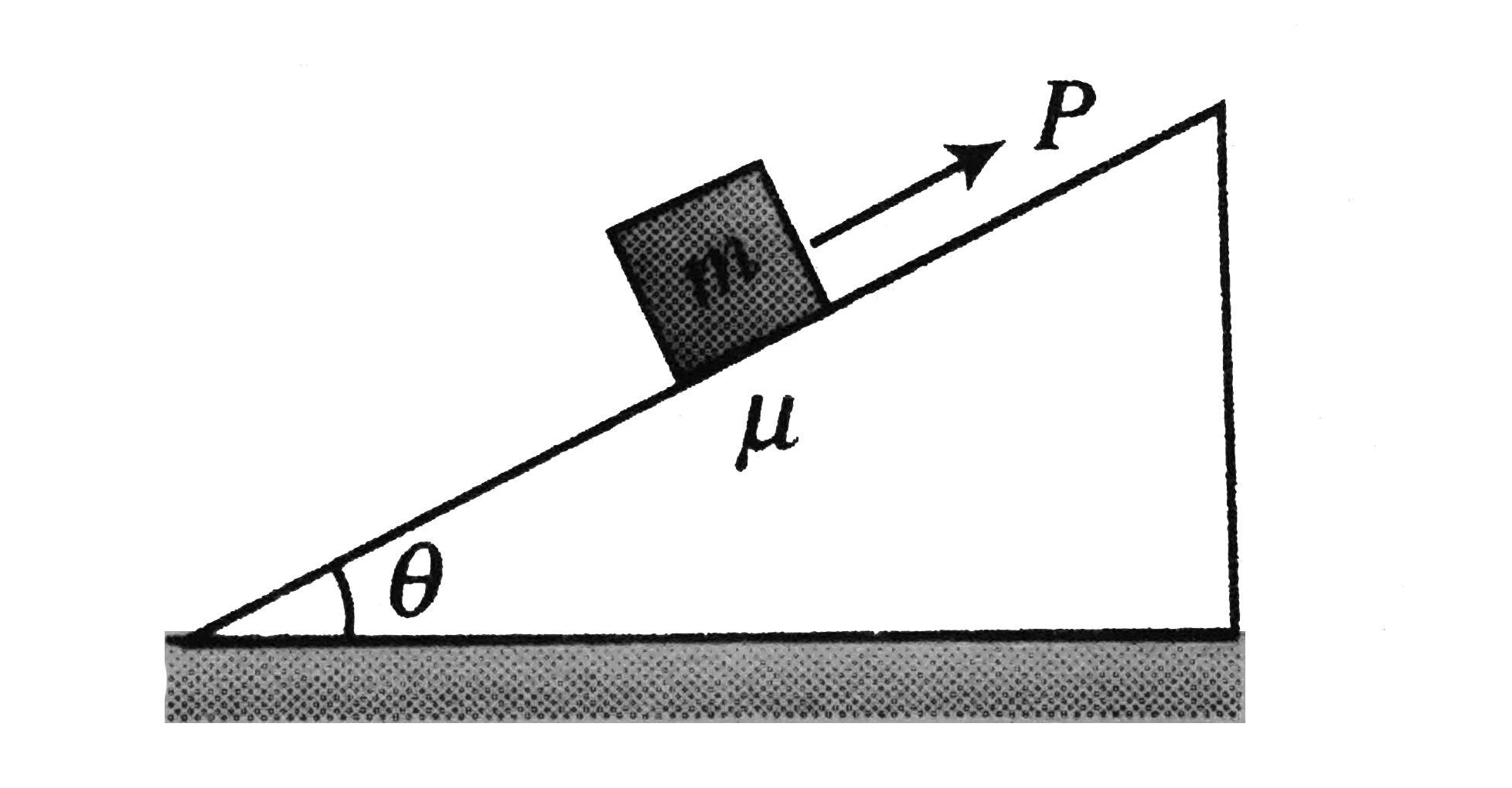
A block of mass $m$ is being pulled up a rough incline by an agent delivering constant power P. The coefficient of friction between the block and the incline is $μ$ . The maximum speed of the block during the course of ascent is

Video Solution

Text Solution

Verified by Experts

$a_{monkey / rope} = g / 4$
Let acceleration of $M = a_{0}$
So, acceleration of rope $= a_{0}$
${\to a}_{monkey} = {\to a}_{monkey / rope} + {\to a}_{rope} = (a_{0} - g / 4)$
Now for mass $M$ , $T - μ M g = M a_{0}$ ……( $1$ )
For monkey $m g - T = m (a_{0} - g / 4)$ ......( $2$ )
From equation ( $1$ ) and ( $2$ )
$m g - μ M g = a_{0} (M + m) - \frac{m g}{4}$
$\Rightarrow a_{0} = (\frac{5 m}{4} - μ M) g / (M + m) = \frac{(5 m - 4 μ M) g}{4 (M + m)}$
$∴ T = \frac{M (5 m - 4 μ M) g}{4 (M + m)} + μ M g$

Updated on:21/07/2023

A block of mass 2kg rests on a rough inclined plane making an angle of $30^{\circ}$ with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
A10.3N
B23.8N
C11.9N
D6.3N
A block of mass 3 kg rests on a rough inclined plane making an angle of $30^{\circ}$ . With the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
A9.8 N
B $0.7 \times 9.8 \times \sqrt{3}$ N
C $9.8 \times \sqrt{3}$ N
D $0.7 \times 9.8$ N