Question

The potential energy function for the force between two in a diatomic molecule can approximately be expressed as $U\left(x\right)=\frac{a}{x^{12}}-\frac{b}{x^4}$, where $a$ and $b$ are positive constants, and $x$ is the distance between the atoms. Answer the following question by selecting most appropriate alternative.
The graph between potential energy vs $x$ will be

Options

A.
B.
C.
D.

Explanation

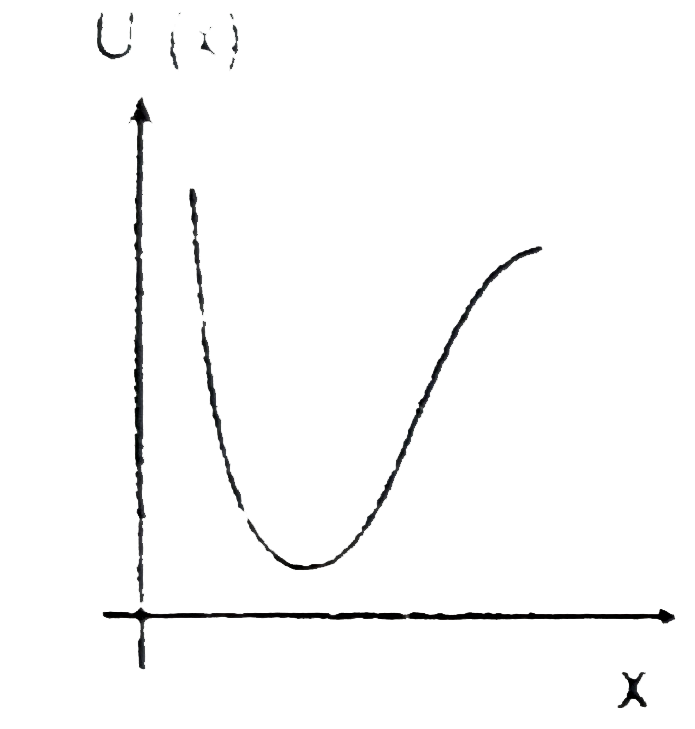
To analyze the potential energy function $$U\left(x\right)=\frac{a}{x^{12}}-\frac{b}{x^4}$$ for a diatomic molecule, we will follow these steps:

Step 1: Analyze the behavior of \( U(x) \) as \( x \) approaches 0 and infinity
- As \( x \to 0 \):
- The term \( \frac{a}{x^{12}} \) dominates and approaches \( +\infty \).
- Therefore, \( U(x) \to +\infty \).

- As \( x \to \infty \):
- The term \( \frac{b}{x^{4}} \) approaches 0.
- Therefore, \( U(x) \to 0 \).

Step 2: Find critical points by differentiating \( U(x) \)
- Differentiate \( U(x) \) with respect to \( x \):
\( \frac{dU}{dx} = -\frac{12a}{x^{13}} + \frac{4b}{x^{5}} \)
- Set the derivative equal to zero to find critical points:
\( -\frac{12a}{x^{13}} + \frac{4b}{x^{5}} = 0 \)
Rearranging gives:
\( \frac{4b}{x^{5}} = \frac{12a}{x^{13}} \)
Multiplying both sides by \( x^{13} \):
\( 4bx^{8} = 12a \)
Simplifying gives:
\( x^{8} = \frac{3a}{b} \)
Therefore:
\( x = \left(\frac{3a}{b}\right)^{\frac{1}{8}} \)

Step 3: Determine the nature of the critical points
- To determine whether this critical point is a minimum or maximum, we can analyze the second derivative:
\( \frac{d^2U}{dx^2} = \frac{156a}{x^{14}} + \frac{20b}{x^{6}} \)
- Since both terms are positive for \( x > 0 \), the second derivative is positive, indicating that the critical point is a minimum.

Step 4: Sketch the graph of \( U(x) \)
- The graph of \( U(x) \) will start at \( +\infty \) when \( x \to 0 \), decrease to a minimum at \( x = \left(\frac{3a}{b}\right)^{\frac{1}{8}} \), and then approach 0 as \( x \to \infty \.

Conclusion The graph of potential energy \( U(x) \) vs. distance \( x \) will start from \( +\infty \), decrease to a minimum, and then approach 0 as \( x \) increases. Therefore, the correct option is that the graph will have a shape that starts high, dips down to a minimum, and then levels off towards zero.