Question

The potential energy function for the force between two in a diatomic molecule can approximately be expressed as $U\left(x\right)=\frac{a}{x^{12}}-\frac{b}{x^4}$, where $a$ and $b$ are positive constants, and $x$ is the distance between the atoms. Answer the following question by selecting most appropriate alternative.
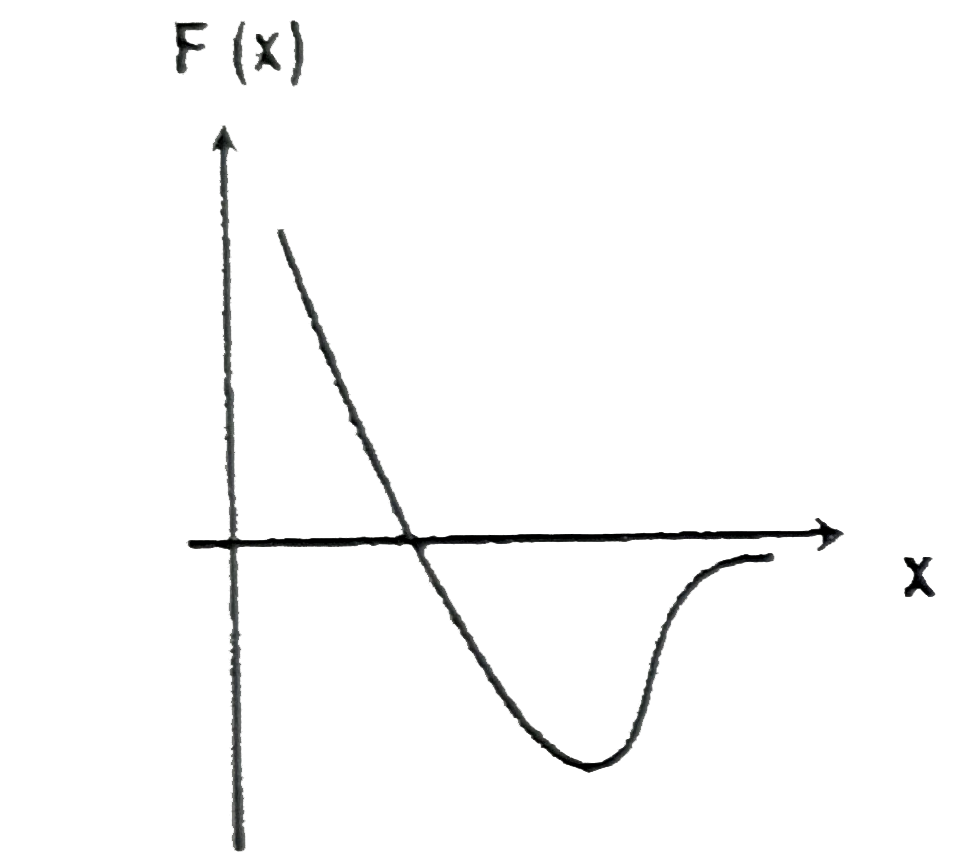
The graph between force between the atoms $\left[F\left(x\right)\right]$ vs $x$ will be

Options

A.
B.
C.
D.

Explanation

To solve the problem, we need to analyze the potential energy function given and derive the corresponding force function. The potential energy function is given by:

$$U\left(x\right)=\frac{a}{x^{12}}-\frac{b}{x^4}$$

Step 1: Derive the Force Function
The force \( F(x) \) can be derived from the potential energy function using the relation:

\( F(x) = -\frac{dU}{dx} \)

Now, we differentiate \( U(x) \):

1. Differentiate \( \frac{a}{x^{12}} \):
\( \frac{d}{dx}\left(\frac{a}{x^{12}}\right) = -12 \cdot \frac{a}{x^{13}} = -\frac{12a}{x^{13}} \)

2. Differentiate \( -\frac{b}{x^{4}} \):
\( \frac{d}{dx}\left(-\frac{b}{x^{4}}\right) = 4 \cdot \frac{b}{x^{5}} = \frac{4b}{x^{5}} \)

Combining these results, we have:

\( F(x) = -\left(-\frac{12a}{x^{13}} + \frac{4b}{x^{5}}\right) = \frac{12a}{x^{13}} - \frac{4b}{x^{5}} \)

Step 2: Analyze the Behavior of the Force Function
Now, we need to analyze the behavior of \( F(x) \) as \( x \) approaches different limits.

1. As \( x \to 0 \):
- The term \( \frac{12a}{x^{13}} \) approaches \( +\infty \) (since \( a \) is positive).
- The term \( -\frac{4b}{x^{5}} \) also approaches \( -\infty \).
- Therefore, \( F(x) \to +\infty \).

2. As \( x \to \infty \):
- Both terms \( \frac{12a}{x^{13}} \) and \( -\frac{4b}{x^{5}} \) approach \( 0 \).
- Therefore, \( F(x) \to 0 \).

3. Finding the Point Where \( F(x) = 0 \):
- Set \( F(x) = 0 \):
\( \frac{12a}{x^{13}} - \frac{4b}{x^{5}} = 0 \)
- Rearranging gives:
\( \frac{12a}{x^{13}} = \frac{4b}{x^{5}} \implies 12a = 4b \cdot x^{8} \implies x^{8} = \frac{3a}{b} \)
- Thus, there exists a non-zero value of \( x \) where \( F(x) = 0 \).

Step 3: Conclusion on the Graph of \( F(x) \)
From the analysis:
- \( F(x) \to +\infty \) as \( x \to 0 \)
- \( F(x) = 0 \) at some finite \( x \)
- \( F(x) \to 0 \) as \( x \to \infty \)

This implies that the graph of \( F(x) \) will start from \( +\infty \), decrease to zero at a certain point, and then approach zero again as \( x \) increases.

Final Answer
The graph of the force \( F(x) \) vs \( x \) will have the following characteristics:
- Starts from \( +\infty \) when \( x \) is close to \( 0 \)
- Crosses the x-axis at a certain point (where \( F(x) = 0 \))
- Approaches \( 0 \) as \( x \) approaches \( \infty \)

Thus, the most appropriate alternative for the graph is option A (as described in the video).