Find the natural frequency of the system as shown in the figure. The pulleys are massless and frictionless.
(Take and )

To find frequency we have to first calculate the acceleration of the block as a function of displacement. In such type of complicated systems we can find this by using the equation of energy conservation and then differentiating it. One important point is to be noted is that the spring is already stretched by some amount and beyond this extension we can not take energy to be equal to so we have to first find out the initial extension.
,
,
If suppose the block is further pulley down by , spring stretches by
(Total energy of system)
.

Topper's Solved these Questions
Similar Questions
Knowledge Check
Find the natural frequency of oscillation of the system as shown in figure. Pulleys are massless and frictionless. Spring and string are also massless. (Take π2=10)
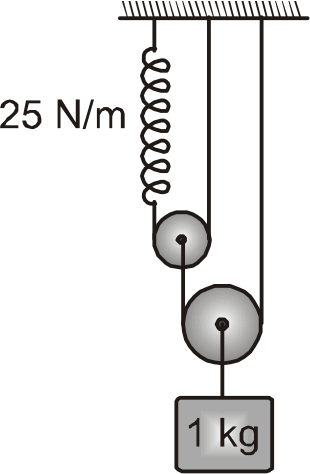 Aπ2HzB√πHzC10√πHzDπHz
Aπ2HzB√πHzC10√πHzDπHzFind the acceleration of the block of mass m. Assume pulleys are massless and frictionless.
 Ag/3B2g3Cg2DNone
Ag/3B2g3Cg2DNoneIn the system shown in figure mB=4kg , and mA=2kg . The pulleys are massless and friction is absent everywhere. The acceleration of block A is.
 A10/3m/s2B20/3m/s2C2m/s2D4m/s2
A10/3m/s2B20/3m/s2C2m/s2D4m/s2
Find the natural frequency of oscillation of the system as shown in figure. Pulleys are massless and frictionless. Spring and string are also massless. (Take π2=10)

View SolutionThere is a system of infinite pulleys and springs.Spring constants are in GP as k 2k 4k 8k.........oo as shown in the figure.All the pulleys are massless frictionless and strings are massless and inextensible.Then time period of small oscillations of the block will be (Mass of block is m ). qquad (in ) (i) 2
View SolutionFind the relation between acceleration of the two blocks m1andm2. Assume pulleys are massless and frictionless and the strings are inextensible .
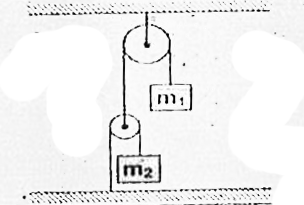
View SolutionFind the relation between acceleration of the two blocks m1andm2. Assume pulleys are massless and frictionless and the strings are inextensible .

View SolutionIn the system shown in fig the pulley is frictionless and the string massless if m1=m2 thrust on the pulley will be:

View Solution

