A charge −Q is unformly distributed over a non-conducting semi-circular rod of radius R. The potential at the center is
0
−Q4πε0R
Q4πε0(2R)
2Q4πε0R
To find the electric potential at the center of a non-conducting semi-circular rod with a uniformly distributed charge of −Q, we can follow these steps:
1. Understanding the Setup:
We have a semi-circular rod with a radius R and a total charge of −Q uniformly distributed along its length. The center of the semi-circle is the point where we want to calculate the electric potential.
2. Charge Element:
Consider a small charge element dq on the semi-circular rod. The total charge −Q is uniformly distributed, so we can express dq in terms of the linear charge density λ:
λ=−QL
where L is the length of the semi-circular rod. The length of the semi-circle is L=πR, thus:
λ=−QπR
Therefore, the small charge element dq can be expressed as:
dq=λds
where ds is an infinitesimal arc length.
3. Potential Contribution from dq:
The electric potential dV at the center due to the charge element dq is given by:
dV=kdqr
where k is Coulomb's constant (k=14πϵ0) and r is the distance from dq to the center. For our semi-circular rod, r=R.
4. Integrating Over the Semi-Circle:
To find the total potential V at the center, we need to integrate dV over the entire semi-circular rod:
V=∫dV=∫kdqR
Substituting dq:
V=∫kλdsR
Since ds=Rdθ (where θ is the angle in radians), we can rewrite the integral:
V=∫π0kλRdθR=∫π0kλdθ
5. Evaluating the Integral:
Substituting λ=−QπR:
V=k(−QπR)∫π0dθ=k(−QπR)⋅π=−kQR
6. Final Result:
Therefore, the potential at the center of the semi-circular rod is:
V=−kQR
We have a semi-circular rod with a radius R and a total charge of −Q uniformly distributed along its length. The center of the semi-circle is the point where we want to calculate the electric potential.
Consider a small charge element dq on the semi-circular rod. The total charge −Q is uniformly distributed, so we can express dq in terms of the linear charge density λ:
λ=−QL
where L is the length of the semi-circular rod. The length of the semi-circle is L=πR, thus:
λ=−QπR
Therefore, the small charge element dq can be expressed as:
dq=λds
where ds is an infinitesimal arc length.
The electric potential dV at the center due to the charge element dq is given by:
dV=kdqr
where k is Coulomb's constant (k=14πϵ0) and r is the distance from dq to the center. For our semi-circular rod, r=R.
To find the total potential V at the center, we need to integrate dV over the entire semi-circular rod:
V=∫dV=∫kdqR
Substituting dq:
V=∫kλdsR
Since ds=Rdθ (where θ is the angle in radians), we can rewrite the integral:
V=∫π0kλRdθR=∫π0kλdθ
Substituting λ=−QπR:
V=k(−QπR)∫π0dθ=k(−QπR)⋅π=−kQR
Therefore, the potential at the center of the semi-circular rod is:
V=−kQR
Similar Questions
Charge q is uniformly distributed over a thin half ring of radius R. The electric field at the centre of the ring is
View SolutionA positive charge Q is uniformly distributed along a circular ring of radius R.a small test charge q is placed at the centre of the ring.

View SolutionA positive charge Q is uniformly distributed along a circular ring of radius R.a small test charge q is placed at the centre of the ring .The

View SolutionA charge q is uniformly distributed on a non-conducting disc of radius R. It is rotated with an angular speed co about an axis passing through the centre of mass of the disc and perpendicular to its plane. Find the magnetic moment of the disc.
View SolutionA charge q is uniformly distributed over a quarter circular ring of radius r. The magnitude of electric field strength at the centre of the ring will be
View SolutionCharge Q is uniformly distributed on a dielectric rod AB of length 2l. The potential at P shown in the figure is equal to

View SolutionCharge Q is uniformly distributed throughout the volume of a solid hemisphere of radius R metres. Then the potential at centre O of hemisphere in volts is:
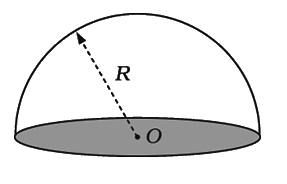
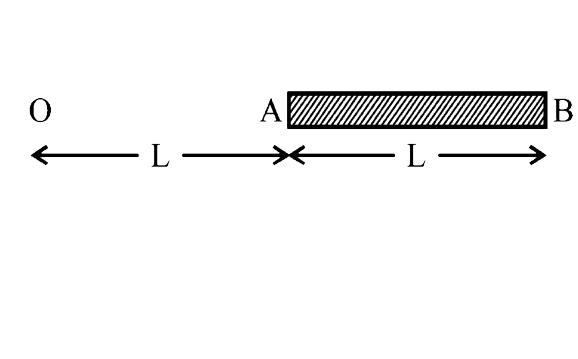
View SolutionA charge Q is uniformly distributed over a long rod AB of length L as shown in the figure. The electric potential at the point O lying at distance L from the end A is
View SolutionA charge Q is uniformly distributed over the surface of two conducting concentric spheres of radii R and r (Rgtr). Then, potential at common centre of these spheres is
View SolutionA charge of 5 nC is uniformly distributed on a ring of radius 4 cm. Find the potential at the axis at a distance of 3 cm from the center.
View Solution