A conducting rod is bent as a parabola y=Kx2, where K is a constant and it is placed in a unifrom magnetic field of induction B. At t=0 a conductor of resistance per unit length λ starts sliding up on the parabola with a constant acceleration a and the parabolic frame starts rotating with constant angular frequency ω about the axis of symmetry, as shown in the figure. Find the instantaneous current induced in the rod, when the frame turns through π/4rad.
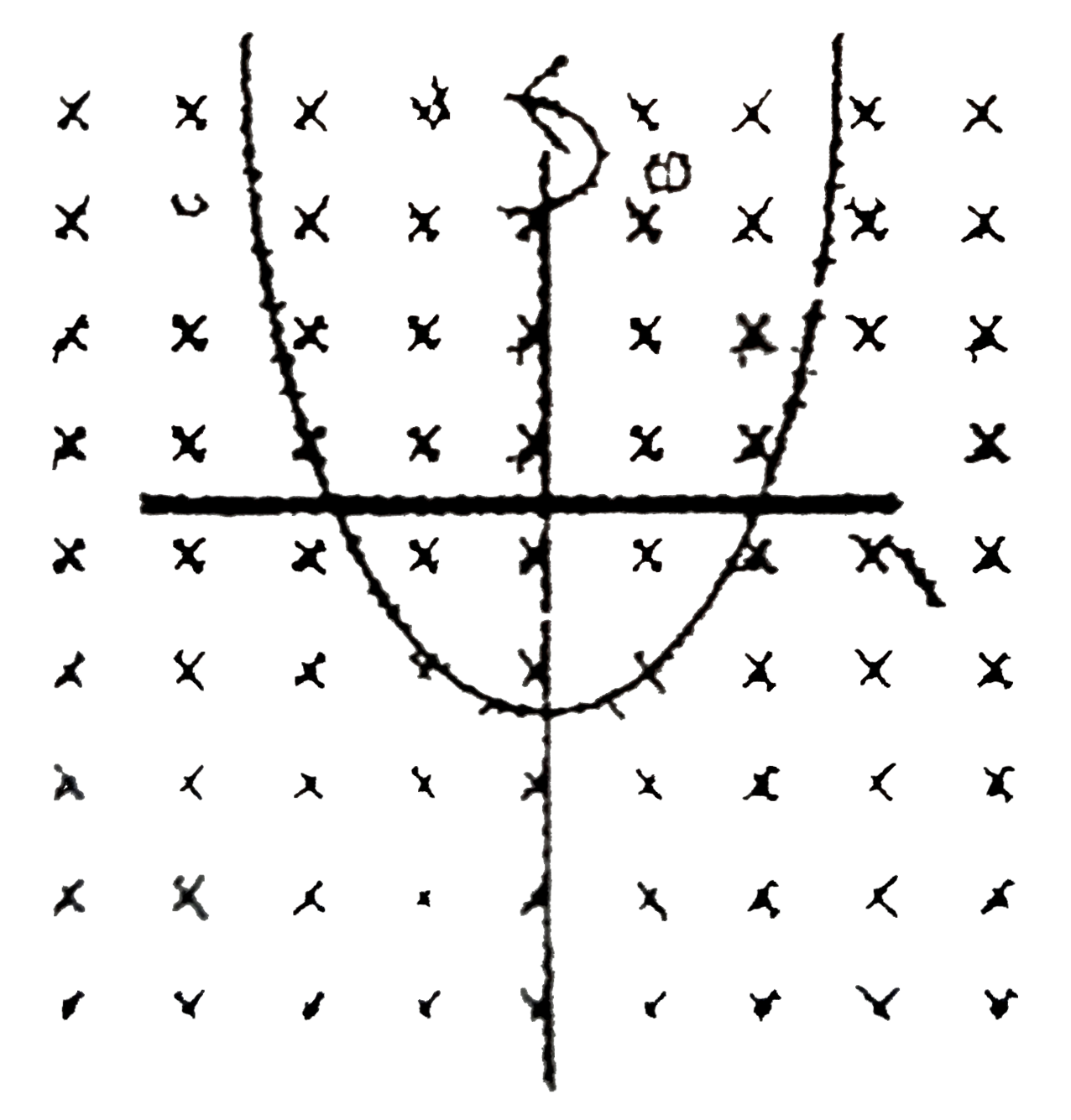
When the frame has turned through an angle θ,
Φ=BAcosθ
where A=∫y02xdy=2√k∫y0√ydy=43√ky3/2
Since y=12at2
∴Φ=B3√2Ka3/2t3cosθ
By Faraday's law, Eind=−dΦdt
or Eind=Ba3/23√2K[t3sinθ(dθdt)−3t2cosθ]
When the frame thus through π/4,
t=θω=π4ω
Eind=Ba3/23√2Kt2[ωtsinθ−3cosθ]
or Eind=π2Ba3/248√2K[π4−3]1√2
Eind=π2(π−12)Ba3/2192ω2√k
I=EindR=π2(π−12)Ba3/2192ω2R√k
R=λ2x=λ.2√yk=2λ√k√a2t=√2akλπ4ω
I=EindR=π2(π−12)Ba3/2√k4ω192ω2√k√2πλ=Baπ(π−12)48√2ωλ
Similar Questions
A rod is rotating with angular velocity ω about axis AB. Find cosθ.
 View Solution
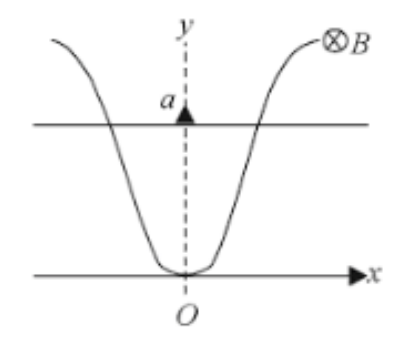
View SolutionA wire bent as a parabola y=kx2 is located in a uniform magnetic field of induction B, the vector B being perpendicular to the plane xy. At t=0, the sliding wire starts sliding from the vertex O with a constant acceleration a linearly as shown in Fig. Find the emf induced in the loop -
 View Solution
View SolutionA conducting rod of length l is rotating with constant angular velocity ω about point O in a uniform magnetic field B as shown in the figure . What is the emf induced between ends P and Q ?
 View Solution
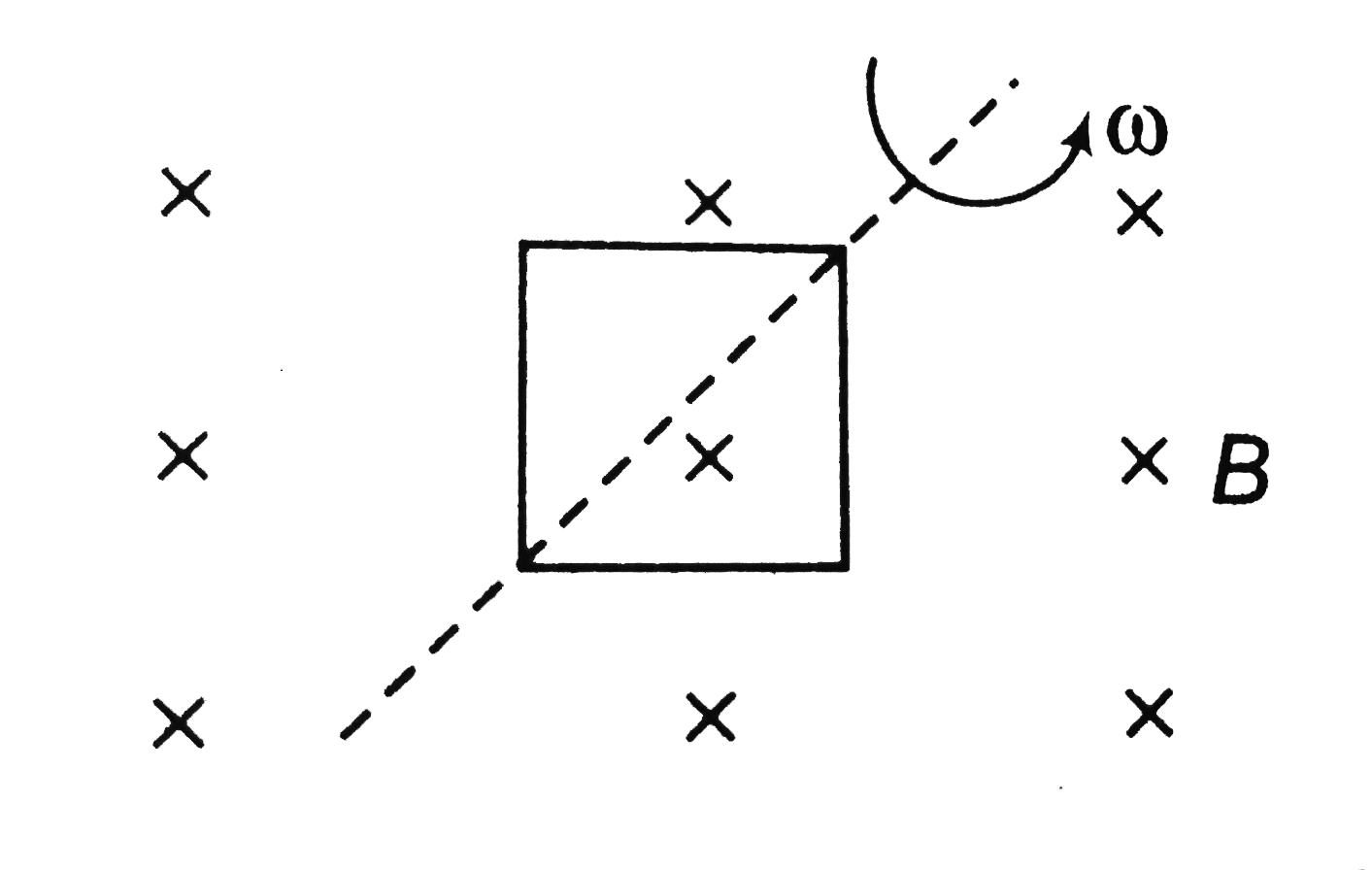
View SolutionA square loop of side b is rotated in a constant magnetic field B at angular frequency ω as shown in the figure. What is the emf induced in it?
 View Solution
View SolutionA wire bent as a parabola y=ax2 is located in a uniformed magnetic field of induaction B , the vector B being perpendicular to the plane x−y . At moment t=0 a connector starts sliding translationwise from the parabola apex with a constant acceleration ω . Find the emf of electromagnetic induction in the loop thus formed as a function of y
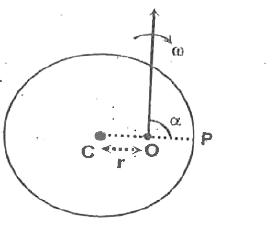
View SolutionRing is fixed on the horizontal surface and a rod starts rotatiing with constant angular velocity ω fixed at O as shown in the figure. Find the magnitude of velocity of intersection points of rod and ring when aplha become 90∘
 View Solution
View Solution
The kinetic energy of a uniform rod of mass m rotating with constant angular velocit ω about one of its end which is fixed as shown in figure is mω2l2N find NView SolutionA hollow non conducting sphere of radius R has a positive charge q uniformly distributed on its surface. The sphere starts rotating with a constant angular velocity 'ω' about an axis passing through center of sphere, as shown in the figure. Then the net magnetic field at center of the sphere is
 View Solution
View SolutionFor an L shaped conducting rod placed in an uniform magnetic field →B rotating with constant angular velocity ω about an axis passing through one of its ends A and normal to the plane of the conductor induced emf
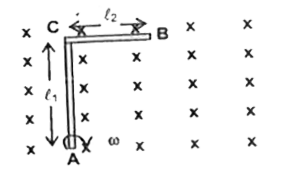 View Solution
View SolutionA rod is rotating with a constant angular velocity ω about point O (its centre) in a magnetic field B as shown. Which of the folloiwng figure correctly shows the distribution of charge inside the rod?
 View Solution
View Solution

