A wire bent as a parabola y=ax2 is located in a uniformed magnetic field of induaction B , the vector B being perpendicular to the plane x−y . At moment t=0 a connector starts sliding translationwise from the parabola apex with a constant acceleration ω . Find the emf of electromagnetic induction in the loop thus formed as a function of y
The correct Answer is:A, B
To solve the problem step by step, let's break down the process of finding the induced electromotive force (emf) in the given scenario.
Step 1: Understand the Setup
We have a wire bent in the shape of a parabola described by the equation y=ax2. The wire is placed in a uniform magnetic field B, which is perpendicular to the x-y plane. A connector starts sliding from the apex of the parabola with a constant acceleration ω.
Step 2: Determine the Position of the Connector
At time t, the distance y covered by the connector can be expressed using the equation of motion:
y=12ωt2
From this, we can solve for t:
t=√2yω
Step 3: Calculate the Velocity of the Connector
The velocity v of the connector at time t can be calculated using:
v=ωt
Substituting the expression for t:
v=ω√2yω=√2ωy
Step 4: Find the Length of the Wire in Motion
The effective length L of the wire that is moving is determined by the parabola's equation. From y=ax2, we can express x in terms of y:
x=√ya
Thus, the effective length of the connector is:
L=2x=2√ya
Step 5: Apply Faraday's Law of Electromagnetic Induction
The induced emf E can be calculated using the formula:
E=vBL
Substituting the expressions for v and L:
E=(√2ωy)B(2√ya)
This simplifies to:
E=2B√2ω√y√ya=2B√a√2ωy
Step 6: Final Expression for Induced EMF
Combining the constants, we can express the induced emf as:
E=2B√a√2ωy
This is the required expression for the emf of electromagnetic induction in the loop as a function of y.
We have a wire bent in the shape of a parabola described by the equation y=ax2. The wire is placed in a uniform magnetic field B, which is perpendicular to the x-y plane. A connector starts sliding from the apex of the parabola with a constant acceleration ω.
At time t, the distance y covered by the connector can be expressed using the equation of motion:
y=12ωt2
From this, we can solve for t:
t=√2yω
The velocity v of the connector at time t can be calculated using:
v=ωt
Substituting the expression for t:
v=ω√2yω=√2ωy
The effective length L of the wire that is moving is determined by the parabola's equation. From y=ax2, we can express x in terms of y:
x=√ya
Thus, the effective length of the connector is:
L=2x=2√ya
The induced emf E can be calculated using the formula:
E=vBL
Substituting the expressions for v and L:
E=(√2ωy)B(2√ya)
This simplifies to:
E=2B√2ω√y√ya=2B√a√2ωy
Combining the constants, we can express the induced emf as:
E=2B√a√2ωy
This is the required expression for the emf of electromagnetic induction in the loop as a function of y.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-1 PART 2
51 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-2 PART 1
14 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Problem
12 Videos
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Advanced level problems
31 Videos
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - HLP
40 Videos
Similar Questions
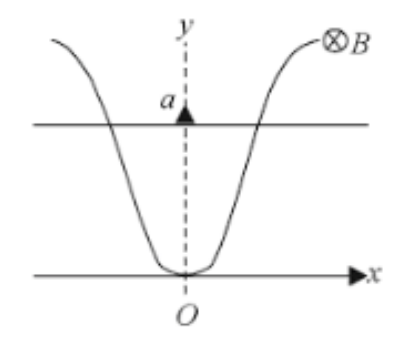
A wire bent as a parabola y=kx2 is located in a uniform magnetic field of induction B, the vector B being perpendicular to the plane xy. At t=0, the sliding wire starts sliding from the vertex O with a constant acceleration a linearly as shown in Fig. Find the emf induced in the loop -
View SolutionA conducting rod is bent as a parabola y=Kx2, where K is a constant and it is placed in a unifrom magnetic field of induction B. At t=0 a conductor of resistance per unit length λ starts sliding up on the parabola with a constant acceleration a and the parabolic frame starts rotating with constant angular frequency ω about the axis of symmetry, as shown in the figure. Find the instantaneous current induced in the rod, when the frame turns through π/4rad.
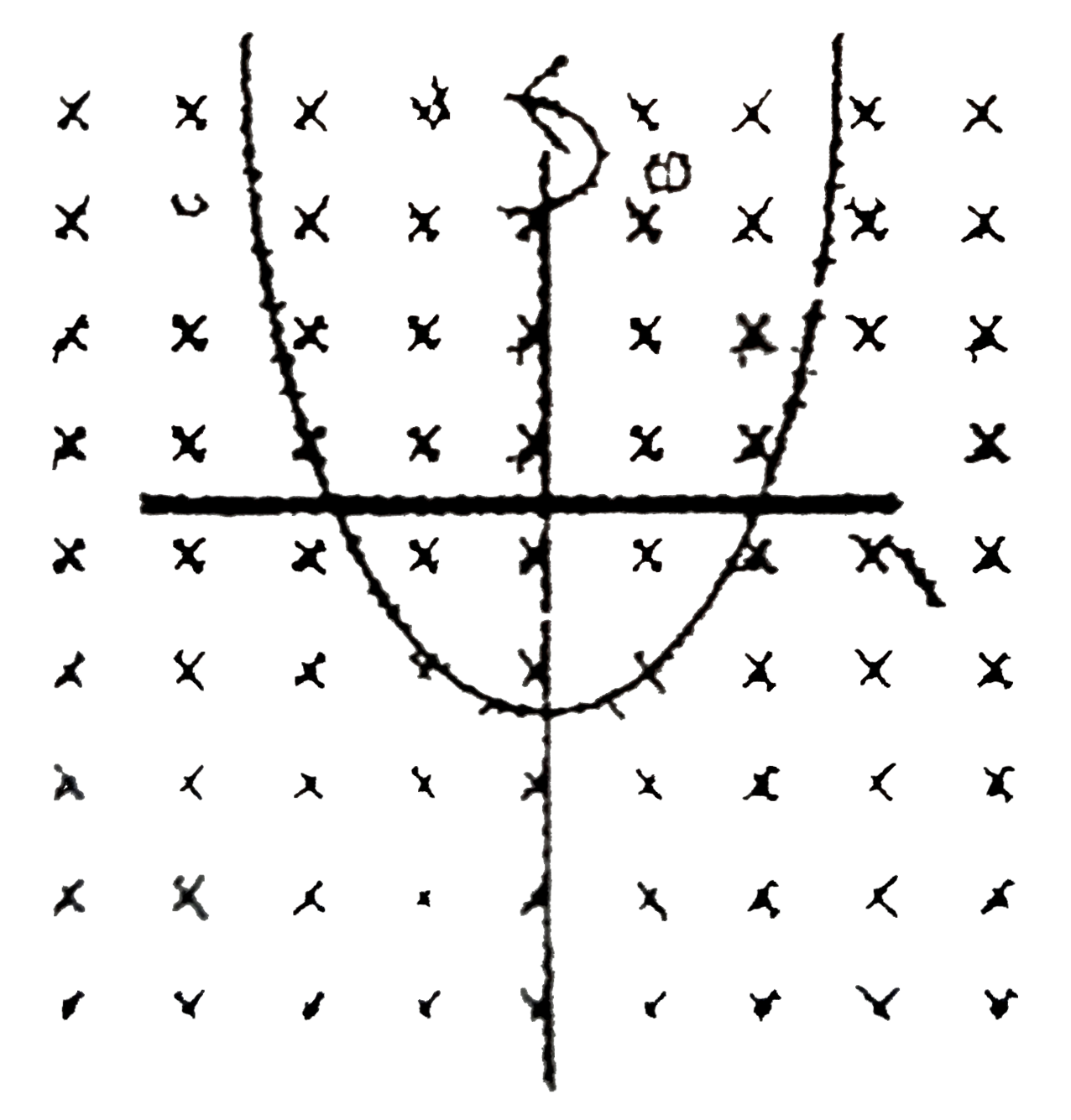
View SolutionA wire loop enclosing a semi-circle of radius a=2cm is located on the boundary of a uniform magnetic field of induction B=1T (figure).At the moment t=0 the loop is set into rotation with a constant angular acceleration β=2rad/sec2 about an axis O coinciding with a line of vector B on the boundary.The emf induced in the loop as a function of time t is [x×10−4(−1)n×t]V, where n=1,2,... is the number of the half-revolution taht the loop performs at the given moment t.Find the value of x.(The arrow in the figure shows the emf direction taken to be positive, at t=0 loop was completely outside)

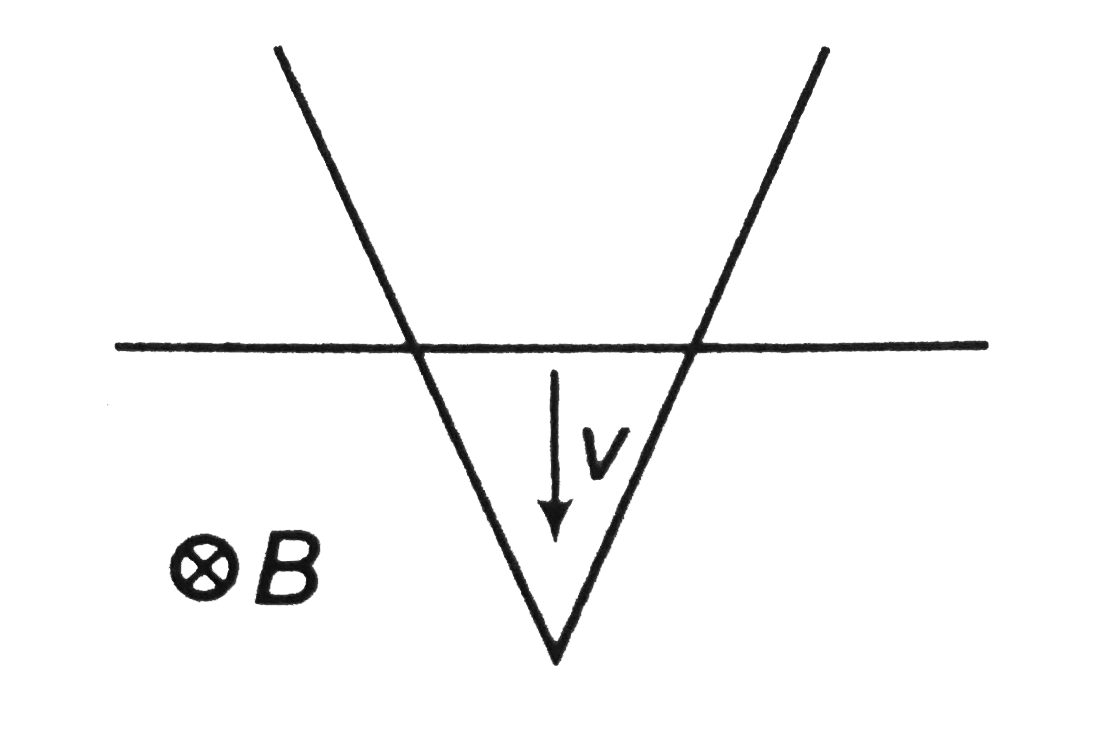
View SolutionA wire is bent in the form of a V shape and placed in a horizontal plane.There exists a uniform magnetic field B perpendicular to the plane of the wire. A uniform conducting rod starts sliding over the V shaped wire with a constant speed v as shown in the figure. If the wire no resistance, the current in rod wil
View SolutionA rectangular loop with a sliding conductor of length l is located in a uniform magnetic field perpendicular to the plane of loop. The magnetic induction perpendicular to the plane of loop Is equal to B. The part ad and be has electric resistance R1 and R2, respectively. The conductor starts moving with constant acceleration a0, at time t=0. Neglecting the self-inductance of the loop and resistance of conductor. Find

(a) the current through the conductor during its motion.
(b) the polarity of abcd terminal.
(c) external force required to move the conductor with the given acceleration.
View SolutionA rectangular loop of length l and breadth b is situated in a uniform magnetic field of induction B with its plane perpendicular to the field as shown in the figure . Calculate the rate of change of magnetic flux and the induced emf if the loop is rotated with constant angular velocity ω
(a) about an axis passing through the centre and perpendicular to the loop.
(b) about an axis passing through the centre parallel to the breadth through angle 180∘ .
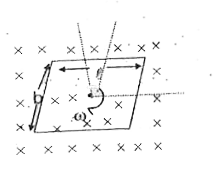
View SolutionA copper rod is bent inot a semi-circle of radius a and at ends straight parts are bent along diameter of the semi-circle and are passed through fixed, smooth and conducting ring O and O' as shown in figure. A capacitor having capacitance C is connected to the rings. The system is located in a uniform magnetic field of induction B such that axis of rotation OO' is perpendicular to the field direction. At initial moment of time (t=0), plane of semi-circle was normal to the field direction and the semi-circle is set in rotation with constant angular velocity ω. Neglect the resistance and inductance of the circuit. The current flowing through the circuit as function of time is

View SolutionA loop of wire enclosing an area S is placed in a region where the magnetic field is perpendicular to the plane. The magnetic field B varies with time according to the expression B=B0e−at where a is some constant. That is, at t=0. The field is B0 and for t>0, the field decreases exponentially. Find the induced emf in the loop as a function of time.
View SolutionA II-shaped conductor is located in a uniform magnetic field perpendicular to the plane of the conductor and varying with time at the rate dBdt=0.10T/s.A conducting connectors starts moving with a constant acceleration w=10cm/s2 along the parallel bars of the conductor.The length of the connector is equal to l=20cm.Find the emf induced (in mV) in the loop t=2.0s after the beginning of the motion.If at the moment t=0 the loop area and the magnetic induction (B) are equal to zero.The self inductance of the loop is to be neglected.
View SolutionA conducting circular loop is placed is a uniform magnetic field B =0.20 T with its plane perpendicular to the field . Somehow, the radius of the loop starts shrinking at a constant rate of 1.0mms−1. Find the induced emf in the loop at an instant when the radius is 2 cm.
View Solution
