(iii)If two circles cut a third circle orthogonally; then the radical axis of two circle will pass through the center of the third circle .
To prove that if two circles cut a third circle orthogonally, then the radical axis of the two circles will pass through the center of the third circle, we can follow these steps:
Step 1: Define the Circles
Let the equations of the three circles be:
- Circle 1: S1:x2+y2+2g1x+2f1y+c1=0
- Circle 2: S2:x2+y2+2g2x+2f2y+c2=0
- Circle 3: S3:x2+y2+2g3x+2f3y+c3=0
Step 2: Orthogonality Condition
The circles S1 and S2 cut the circle S3 orthogonally. The condition for two circles to cut orthogonally is given by:
- For S1 and S3:
2g1g3+2f1f3=c1+c3
- For S2 and S3:
2g2g3+2f2f3=c2+c3
Step 3: Subtract the Two Conditions
Subtract the second equation from the first:
(2g1g3+2f1f3)−(2g2g3+2f2f3)=(c1+c3)−(c2+c3)
This simplifies to:
2g1g3−2g2g3+2f1f3−2f2f3=c1−c2
Factoring out common terms gives:
2g3(g1−g2)+2f3(f1−f2)=c1−c2(1)
Step 4: Radical Axis Equation
The equation of the radical axis of circles S1 and S2 is given by:
S1−S2=0
This expands to:
2(g1−g2)x+2(f1−f2)y+(c1−c2)=0
Step 5: Check if the Radical Axis Passes Through the Center of S3
The center of circle S3 is given by the point (−g3,−f3). We need to check if this point satisfies the radical axis equation:
Substituting x=−g3 and y=−f3 into the radical axis equation:
2(g1−g2)(−g3)+2(f1−f2)(−f3)+(c1−c2)=0
This simplifies to:
−2g3(g1−g2)−2f3(f1−f2)+(c1−c2)=0
Rearranging gives:
2g3(g1−g2)+2f3(f1−f2)=c1−c2
From equation (1), we have:
2g3(g1−g2)+2f3(f1−f2)=c1−c2
Thus, both sides are equal, confirming that the radical axis passes through the center of circle S3.
Conclusion
Hence, we have proved that if two circles cut a third circle orthogonally, then the radical axis of the two circles will pass through the center of the third circle.
---
Let the equations of the three circles be:
- Circle 1: S1:x2+y2+2g1x+2f1y+c1=0
- Circle 2: S2:x2+y2+2g2x+2f2y+c2=0
- Circle 3: S3:x2+y2+2g3x+2f3y+c3=0
The circles S1 and S2 cut the circle S3 orthogonally. The condition for two circles to cut orthogonally is given by:
- For S1 and S3:
2g1g3+2f1f3=c1+c3
- For S2 and S3:
2g2g3+2f2f3=c2+c3
Subtract the second equation from the first:
(2g1g3+2f1f3)−(2g2g3+2f2f3)=(c1+c3)−(c2+c3)
This simplifies to:
2g1g3−2g2g3+2f1f3−2f2f3=c1−c2
Factoring out common terms gives:
2g3(g1−g2)+2f3(f1−f2)=c1−c2(1)
The equation of the radical axis of circles S1 and S2 is given by:
S1−S2=0
This expands to:
2(g1−g2)x+2(f1−f2)y+(c1−c2)=0
The center of circle S3 is given by the point (−g3,−f3). We need to check if this point satisfies the radical axis equation:
Substituting x=−g3 and y=−f3 into the radical axis equation:
2(g1−g2)(−g3)+2(f1−f2)(−f3)+(c1−c2)=0
This simplifies to:
−2g3(g1−g2)−2f3(f1−f2)+(c1−c2)=0
Rearranging gives:
2g3(g1−g2)+2f3(f1−f2)=c1−c2
From equation (1), we have:
2g3(g1−g2)+2f3(f1−f2)=c1−c2
Thus, both sides are equal, confirming that the radical axis passes through the center of circle S3.
Hence, we have proved that if two circles cut a third circle orthogonally, then the radical axis of the two circles will pass through the center of the third circle.
Similar Questions
The radical axis of two circles S=0, S'=0 does not exist if
View SolutionIf z≠1 and z2z−1 is real, then the point represented by the complex number z lies (1) either on the real axis or on a circle passing through the origin (2) on a circle with centre at the origin (3) either on the real axis or on a circle not passing through the origin (4) on the imaginary axis
View Solution
Knowledge Check
AB and CD are chords of the circle, and E and F are the midpoints of the chords, respectively. The line EF passes through the center O of the circle. IF EF=17. then what is radius of the circle?
 A10B12C13D15
A10B12C13D15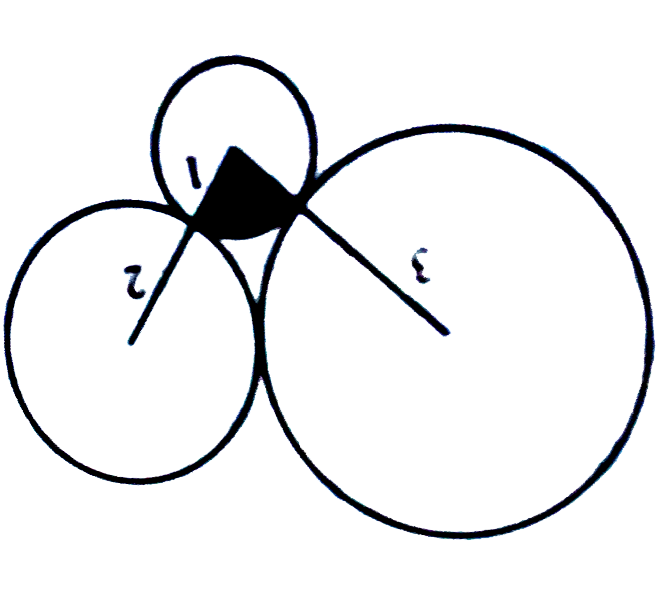
Three circles with radii 1,2 and 3 inches are externally tangent to one another , as shown in the figure above . The area , in square inches , of the sector of the circle of radius 1 that is cut off by the line segments joining the center of that circle to the centers of the other two circles (the shaded area ) isAπBπ2Cπ3Dπ4
If z≠1 and z2z−1 is real, then the point represented by the complex number z lies (1) either on the real axis or on a circle passing through the origin (2) on a circle with centre at the origin (3) either on the real axis or on a circle not passing through the origin (4) on the imaginary axis
View SolutionTwo parallel tangents to a given circle are cut by a third tangent at the points AandB. If C is the center of the given circle, then ∠ACB (a)depends on the radius of the circle. (b)depends on the center of the circle. (c)depends on the slopes of three tangents. (d)is always constant
View SolutionTwo circles with equal radii are intersecting at the points (0, 1) and (0,-1). The tangent at the point (0,1) to one of the circles passes through the centre of the other circle. Then the distance between the centres of these circles is.
View SolutionIf the chord of contact of tangents from a point P to a given circle passes through Q, then the circle on PQ as diameter. cuts the given circle orthogonally touches the given circle externally touches the given circle internally none of these
View SolutionThe centres of the circles are (a, c) and (b, c) and their radical axis is y-axis. The radius of one of the circles is r. The radius of the other circle is
View Solution(a,0) and (b, 0) are centres of two circles belonging to a co-axial system of which y-axis is the radical axis. If radius of one of the circles 'r', then the radius of the other circle is
View Solution
