Two infinitely large sheets having charge densities σ1andσ2 respectively (σ1>σ2) are placed near each other separated by distance 'd'. A small charge 'q' is placed in between two plates such that there is no effect on charge distribution on plates. Now this charge is moved at an angle of 45∘ with the horizontal towards plate having charge density σ2 by distance 'a' (a<<d). Find the work done by electric field in the process.
To solve the problem step by step, we will calculate the work done by the electric field when a charge q is moved between two charged plates.
Step 1: Understand the Electric Field Between the Plates
The electric field E between two infinitely large sheets with surface charge densities σ1 and σ2 (where σ1>σ2) is given by:
E=σ1−σ22ϵ0
where ϵ0 is the permittivity of free space.
Hint: Remember that the electric field due to a single infinite sheet of charge is σ2ϵ0 directed away from the sheet if the charge is positive.
Step 2: Calculate the Force on the Charge q
The force F acting on the charge q due to the electric field E is given by:
F=qE=q(σ1−σ22ϵ0)
Hint: The force on a charge in an electric field is the product of the charge and the electric field strength.
Step 3: Determine the Displacement of the Charge
The charge is moved at an angle of 45∘ towards the plate with charge density σ2 by a distance a. The horizontal component of this displacement dx is:
dx=acos(45∘)=a√2
Hint: Use trigonometric functions to resolve the displacement into components.
Step 4: Calculate the Work Done by the Electric Field
The work done W by the electric field when moving the charge is given by:
W=F⋅dx=(qσ1−σ22ϵ0)⋅(a√2)
Thus, the work done can be expressed as:
W=qa(σ1−σ2)2√2ϵ0
Hint: Work done is calculated as the product of force and displacement in the direction of the force.
Final Answer
The work done by the electric field in moving the charge q is:
W=qa(σ1−σ2)2√2ϵ0
The electric field E between two infinitely large sheets with surface charge densities σ1 and σ2 (where σ1>σ2) is given by:
E=σ1−σ22ϵ0
where ϵ0 is the permittivity of free space.
The force F acting on the charge q due to the electric field E is given by:
F=qE=q(σ1−σ22ϵ0)
The charge is moved at an angle of 45∘ towards the plate with charge density σ2 by a distance a. The horizontal component of this displacement dx is:
dx=acos(45∘)=a√2
The work done W by the electric field when moving the charge is given by:
W=F⋅dx=(qσ1−σ22ϵ0)⋅(a√2)
Thus, the work done can be expressed as:
W=qa(σ1−σ2)2√2ϵ0
The work done by the electric field in moving the charge q is:
W=qa(σ1−σ2)2√2ϵ0
Similar Questions
Two thin infinite parallel plates have uniform charge densities +σ and −σ. The electric field in the space between them is
View SolutionTwo uniformly charged large plane sheets S1 and S2 having charge densities σ1 and σ2 (σ1>σ2) are placed at a distance d parallel to each other. A charge q0 is moved along a line of length a(altd) at an angle 45∘ with the normal to S1. Calculate the work done by the electric field
View SolutionAn injfinite large sheet has charg density σC/m2 Find electric field at a distance d perendicular to the sheet.
View SolutionTwo infinitely long line charges having charge density λ each are parallel to each other and separated by distance d. A charge particle of mass m and charge q is placed at mid point between them. This charge displaced slightly along a line AB which is perpendicular to the line charges and in the plane of the charges. prove that the motion of the particle will be SHM for small displacement and λq>0 Neglect gravity. Find the time period.
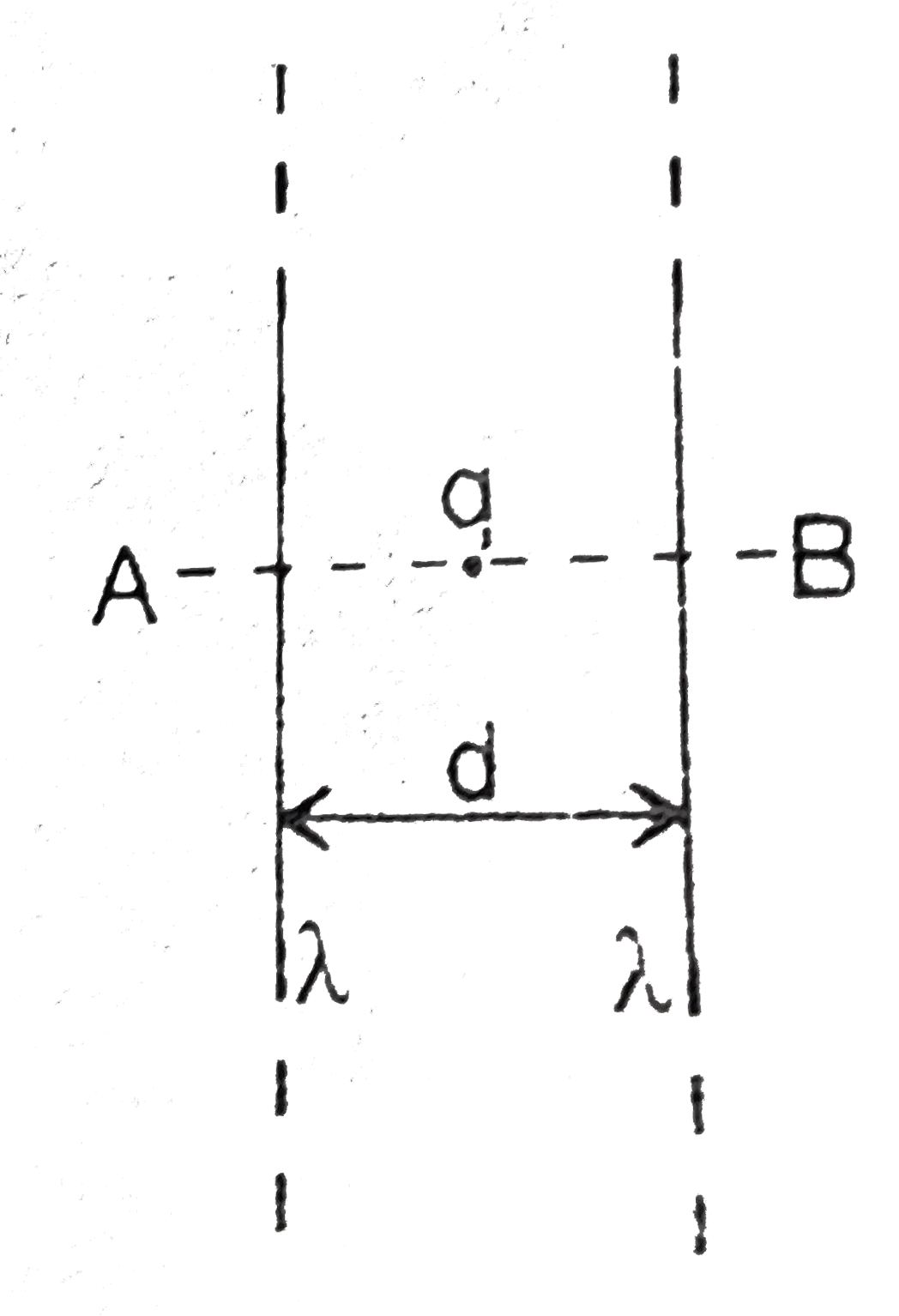 View Solution
View SolutionTwo infinite sheets of unifrom charge density +σand−σ are parallel to each other as shown in the figure. Electric field at the
 View Solution
View SolutionTwo charged thin infinite plane sheets of uniform surface charge density σ+andσ− where |σ+|>|σ−| , intersect right angle Which of the following best represents the electric field lines for this system:
View SolutionTwo paralle plane sheets 1 and 2 carry uniform charge densites σ1andσ2 (see fig. The electric field in the region marked I is (σ1>σ2):
 View Solution
View SolutionTwo plates, each of area A, are placed parallel to each other at a distance d. One plate is connected to a battery of emf E and its negative is earthed. The other plate is also earthed. The charge drawn by plate is
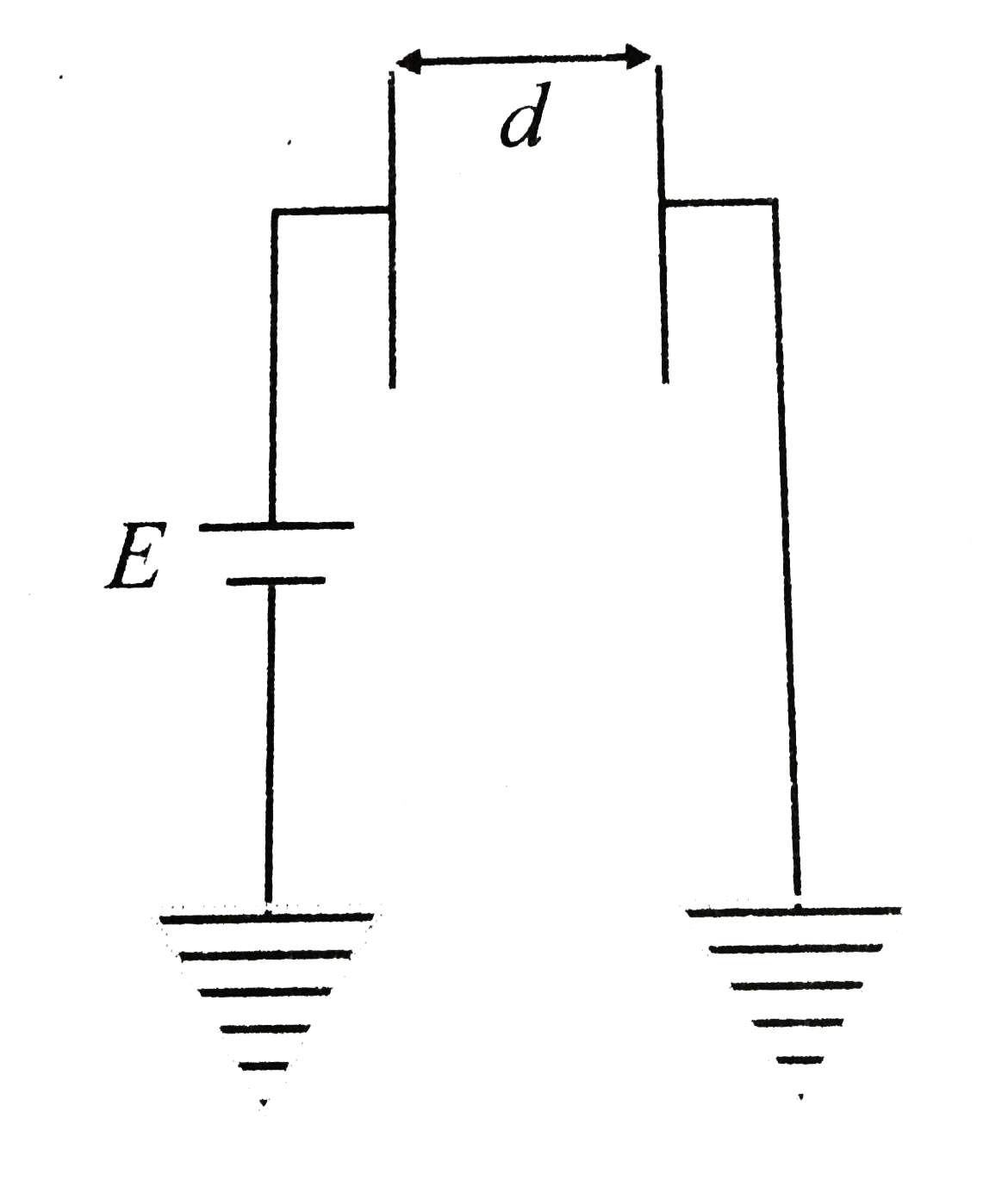 View Solution
View SolutionThree non-conducting large parallel plates have surface charge densities σ,−2σand4σ respectively as shown in the figure. The electric field at the point P is
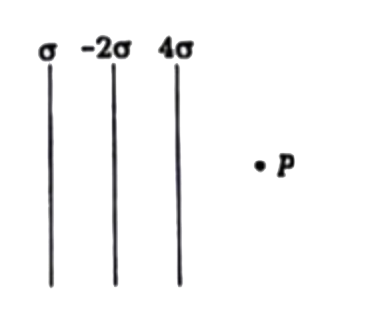 View Solution
View SolutionElectric field intensity at a point in between two parallel sheets with like charges of same surface charge densities (σ) is
View Solution

