Two charged thin infinite plane sheets of uniform surface charge density σ+andσ− where |σ+|>|σ−| , intersect right angle Which of the following best represents the electric field lines for this system:

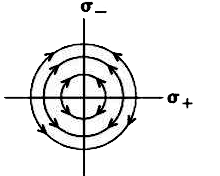
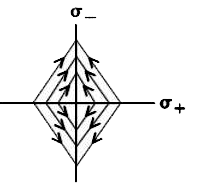
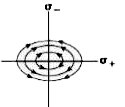
The correct Answer is:A
To solve the problem of determining the electric field lines produced by two intersecting infinite plane sheets with uniform surface charge densities σ+ and σ−, we can follow these steps:
1. Understand the Configuration:
- We have two infinite plane sheets that intersect at right angles.
- One sheet has a positive surface charge density σ+ and the other has a negative surface charge density σ−.
- It is given that |σ+|>|σ−|.
2. Determine the Electric Field Due to Each Sheet:
- The electric field due to an infinite plane sheet with surface charge density σ is given by the formula:
E=σ2ϵ0
where ϵ0 is the permittivity of free space.
- For the positively charged sheet (σ+), the electric field points away from the sheet.
- For the negatively charged sheet (σ−), the electric field points towards the sheet.
3. Calculate the Net Electric Field:
- Since the sheets are intersecting at right angles, we can analyze the electric fields in two perpendicular directions (let's assume the positive sheet is along the y-axis and the negative sheet is along the x-axis).
- The electric field due to the positive sheet (E+) will be directed in the positive y-direction and has a magnitude of:
E+=σ+2ϵ0
- The electric field due to the negative sheet (E−) will be directed in the negative x-direction and has a magnitude of:
E−=σ−2ϵ0
4. Analyze the Direction and Magnitude:
- Since |σ+|>|σ−|, the net electric field will be stronger in the direction of the positive sheet (y-direction) compared to the negative sheet (x-direction).
- Therefore, the electric field lines will be denser in the y-direction and sparser in the x-direction.
5. Sketch the Electric Field Lines:
- Draw the electric field lines originating from the positive sheet and terminating at the negative sheet.
- The lines will be more concentrated in the y-direction due to the greater magnitude of the electric field from the positive sheet.
6. Select the Correct Representation:
- Based on the analysis, the option that shows electric field lines more concentrated in the y-direction and less in the x-direction represents the correct configuration.
Conclusion:
The correct representation of the electric field lines for the given system is the option that shows denser lines in the y-direction and sparser lines in the x-direction.
- We have two infinite plane sheets that intersect at right angles.
- One sheet has a positive surface charge density σ+ and the other has a negative surface charge density σ−.
- It is given that |σ+|>|σ−|.
- The electric field due to an infinite plane sheet with surface charge density σ is given by the formula:
E=σ2ϵ0
where ϵ0 is the permittivity of free space.
- For the positively charged sheet (σ+), the electric field points away from the sheet.
- For the negatively charged sheet (σ−), the electric field points towards the sheet.
- Since the sheets are intersecting at right angles, we can analyze the electric fields in two perpendicular directions (let's assume the positive sheet is along the y-axis and the negative sheet is along the x-axis).
- The electric field due to the positive sheet (E+) will be directed in the positive y-direction and has a magnitude of:
E+=σ+2ϵ0
- The electric field due to the negative sheet (E−) will be directed in the negative x-direction and has a magnitude of:
E−=σ−2ϵ0
- Since |σ+|>|σ−|, the net electric field will be stronger in the direction of the positive sheet (y-direction) compared to the negative sheet (x-direction).
- Therefore, the electric field lines will be denser in the y-direction and sparser in the x-direction.
- Draw the electric field lines originating from the positive sheet and terminating at the negative sheet.
- The lines will be more concentrated in the y-direction due to the greater magnitude of the electric field from the positive sheet.
- Based on the analysis, the option that shows electric field lines more concentrated in the y-direction and less in the x-direction represents the correct configuration.
The correct representation of the electric field lines for the given system is the option that shows denser lines in the y-direction and sparser lines in the x-direction.
Topper's Solved these Questions
Similar Questions
Two large parallel sheets charged uniformly with surfasce charge density σ and −σ are located as shown in the figure. Which one of the following graphs shows the variation of electric field along a line perpendicular to the sheets as one moves from A to B ?

View SolutionTwo infinite sheets of unifrom charge density +σand−σ are parallel to each other as shown in the figure. Electric field at the
View SolutionElectric field due to an infinite non-conducting sheet of surface charge density σ, at a distance r from it is
View SolutionTwo thin infinite parallel plates have uniform charge densities +σ and −σ. The electric field in the space between them is
View SolutionThere are two infinite plane sheets each having uniform surface charge density +σC/m2 They are inclined to each other at an angle 30∘as shown in the figure. Electric field at any arbitrary point P is:

View SolutionThere are two infinite plane sheets each having uniform surface charge density +σC/m2 They are inclined to each other at an angle 30∘as shown in the figure. Electric field at any arbitrary point P is:

View SolutionIf three infinite charged sheets of uniform surface charge densities σ,2σ and −4σ are placed as shown in figure, then find out electric field intensities at points A, B, C and D.

View SolutionA long thin flat sheet has a uniform surface charge density σ. The magnitude of the electric field at a distance .r. from it is given by
View SolutionThe electric field near a conducting surface having a uniform surface charge denstiy σ is given by
View SolutionTwo infinite planes each with uniform surface charge density +σ are kept in such a way that the angle between them is 60°. The electric field in the region shown between them is given by
View Solution
