Two circular rings A and B each of radius a=30cm are placed co-axially with their axes horizontal in a uniform electric field E=105N/C directed vertically upward as shown in the figure. The distance between the centers of these rings A and B is h=40cm. Ring A has a positive charge q1=10μC while ring B has a negative charge of magnitude q2=20μC. A particle of mass m = 100 gm and carrying a positive charge q=10μC is released from rest at the centre of the ring A. Calculate its velocity when it has moved a distance 40 cm.

Weight of the particle W=mg=1001000×10=1 Newton
Force due to electrostatic field E=qE=10×10−6×105=1 Newton.
Thus the weight of the particle is balanced by the electrostatic force.
The particle experiences net force in the through the centers of ring A and B and is accelerated towards the centre of ring B. At the centre of ring B.
KE = Loss of PE
⇒12mv2=UA−UB=14π∈0qq1a+14π∈0q(−q2)√a2+h2−14π∈0qq1√a2+h2−14π∈0q(−q2)a
12mv2=q4π∈0[q1(1a−1√a2+h2)+q2(1a−1√a2+h2)]
=q4π∈0[(q1+q2)(√a2+h2−aa√a2+h2)]
⇒v=
⎷2q(q1+q2)4π∈0m[√a2+h2−aa√a2+h2]
For the given value v=6√2m/s
Similar Questions
Two circular rings A and B each of radius a = 30 cm are placed coaxially with their axis horizontal in a uniform electric field E=105NC−1 directed vertically upward as shown in figure. Distance between centers of the rings A and B (CAandCB)is40cm. Ring A has positive charge qA=10μC and B has a negative charge qB=−20μC. A particle of mass m and charge q=10μC is released from rest at the center of ring A. If particle moves along CACB, then
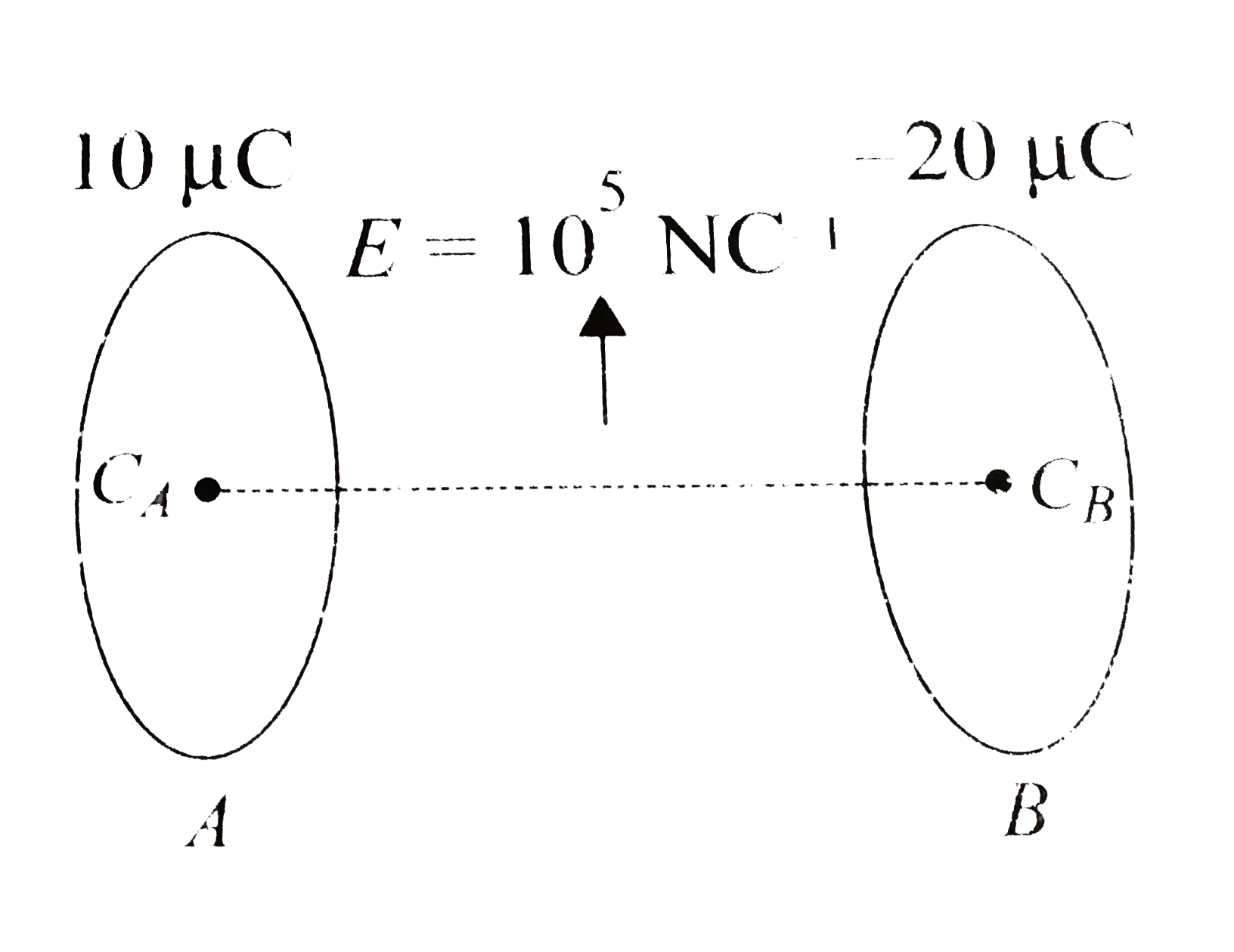
Speed of particle when it reaches at center of B is
View SolutionTwo circular rings A and B each of radius a = 30 cm are placed coaxially with their axis horizontal in a uniform electric field E=105NC−1 directed vertically upward as shown in figure. Distance between centers of the rings A and B (CAandCB)is40cm. Ring A has positive charge qA=10μC and B has a negative charge qB=−20μC. A particle of mass m and charge q=10μC is released from rest at the center of ring A. If particle moves along CACB, then

Work done by electric field, when particle moves from CA→CB is
View Solution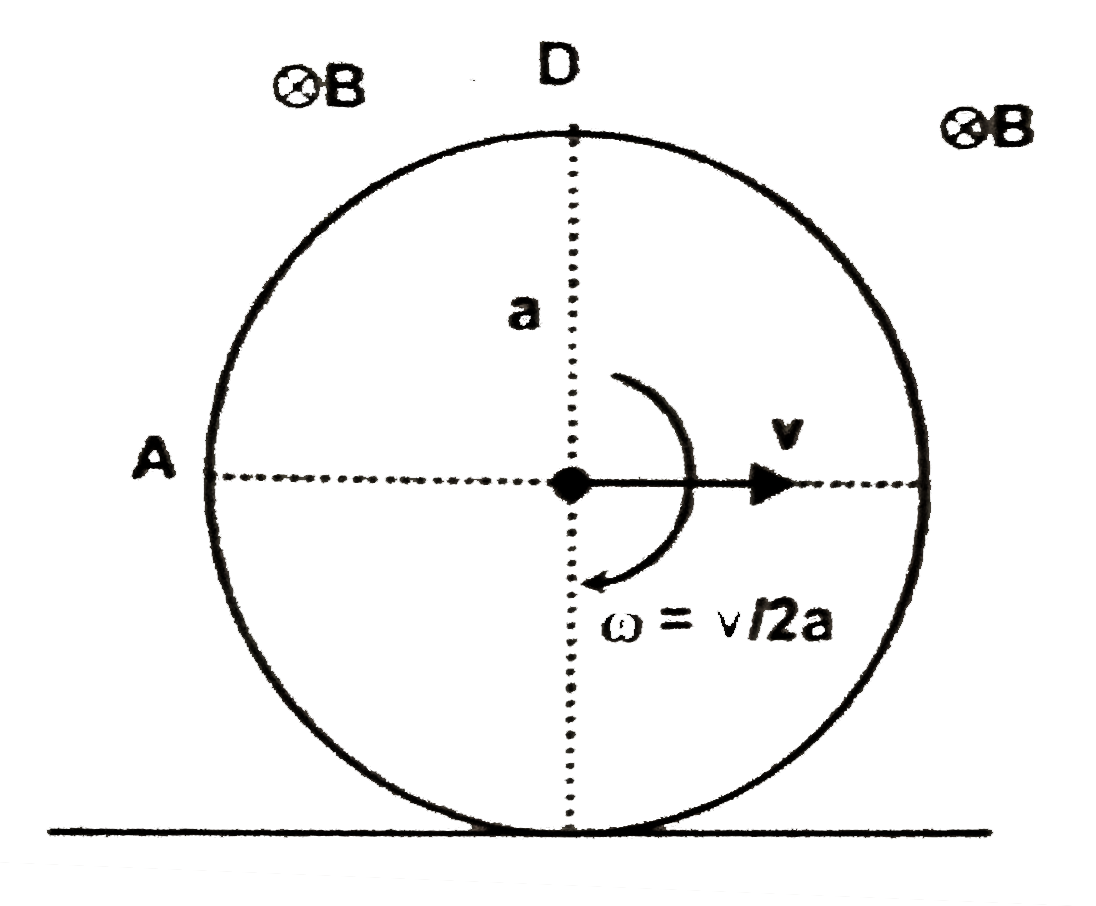
A circular conducting ring of radius 'a' is rolling with slipping on a horizontal surface as shown. A uniform magnetic field B is existing perpendicular to the plane of motion of the ring. The emf iniduced between the points A and D of the ring is
View SolutionA thin circular wire of radius r has a charge Q. If a point charge q is placed at the centre of the ring, then find the increase in tension in the wire.
View SolutionA positive charge Q is uniformly distributed along a circular ring of radius R.a small test charge q is placed at the centre of the ring.

View SolutionA positive charge Q is uniformly distributed along a circular ring of radius R.a small test charge q is placed at the centre of the ring .The

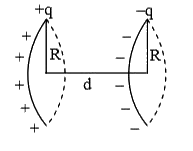
View SolutionTwo thin rings each of radius R are placed at a distance 'd' apart. The charges on the rings are +q and -q. The potential difference between their centres will be -
View SolutionPositive and negative charges of 1μC each are placed at two points as shown in the figure. Find the potential difference between A and B
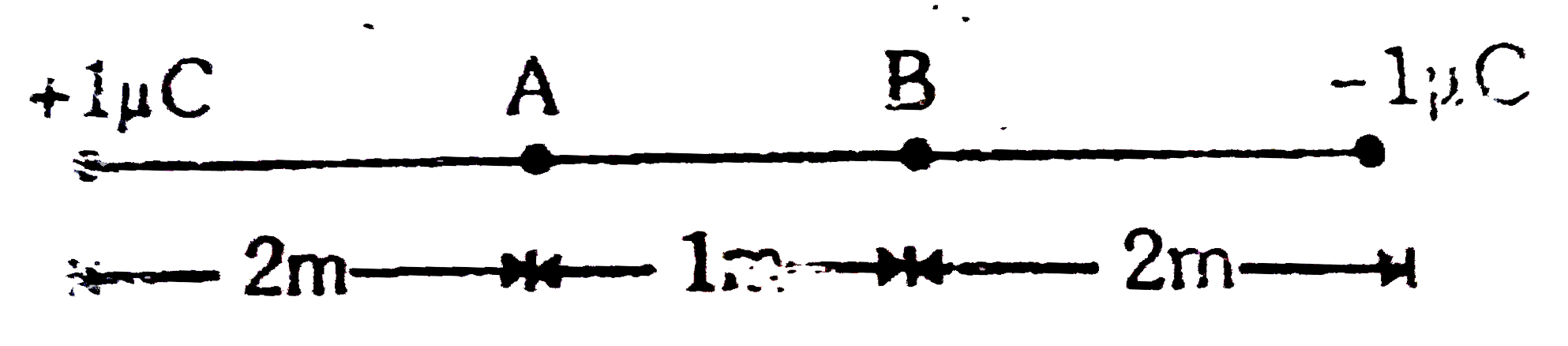
View SolutionTwo identical charges, 5μC each are fixed at a distance 8 cm and a charged particle of mass 9×10−6kg and charge −10μC is placed at a distance 5 cm from each of them and is released. Find the speed of the particle when it is nearest to the two charges.
View SolutionA regular hexagon of side 10 cm has a charge 5μC at each of its vertices. Calculate the potential at the center of the hexagon.
View Solution
