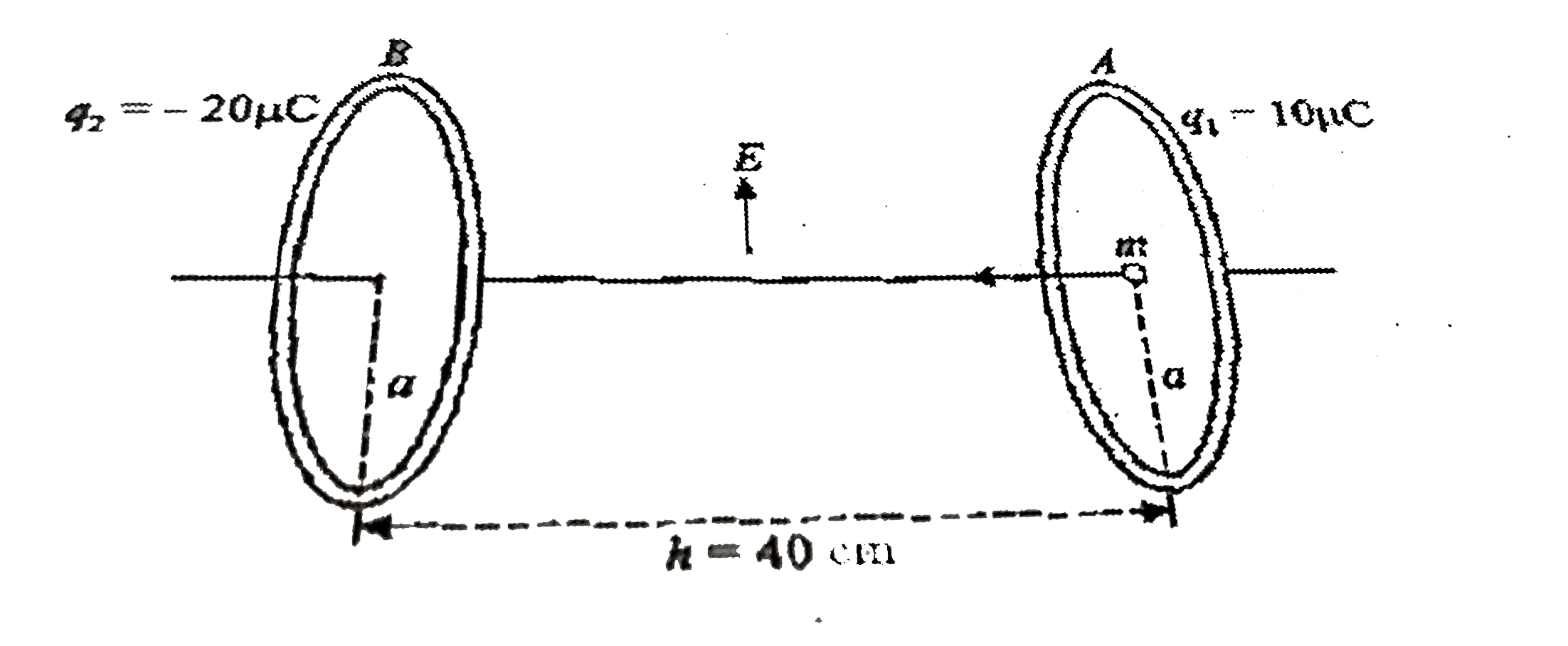
Two circular rings A and B each of radius a = 30 cm are placed coaxially with their axis horizontal in a uniform electric field E=105NC−1 directed vertically upward as shown in figure. Distance between centers of the rings A and B (CAandCB)is40cm. Ring A has positive charge qA=10μC and B has a negative charge qB=−20μC. A particle of mass m and charge q=10μC is released from rest at the center of ring A. If particle moves along CACB, then
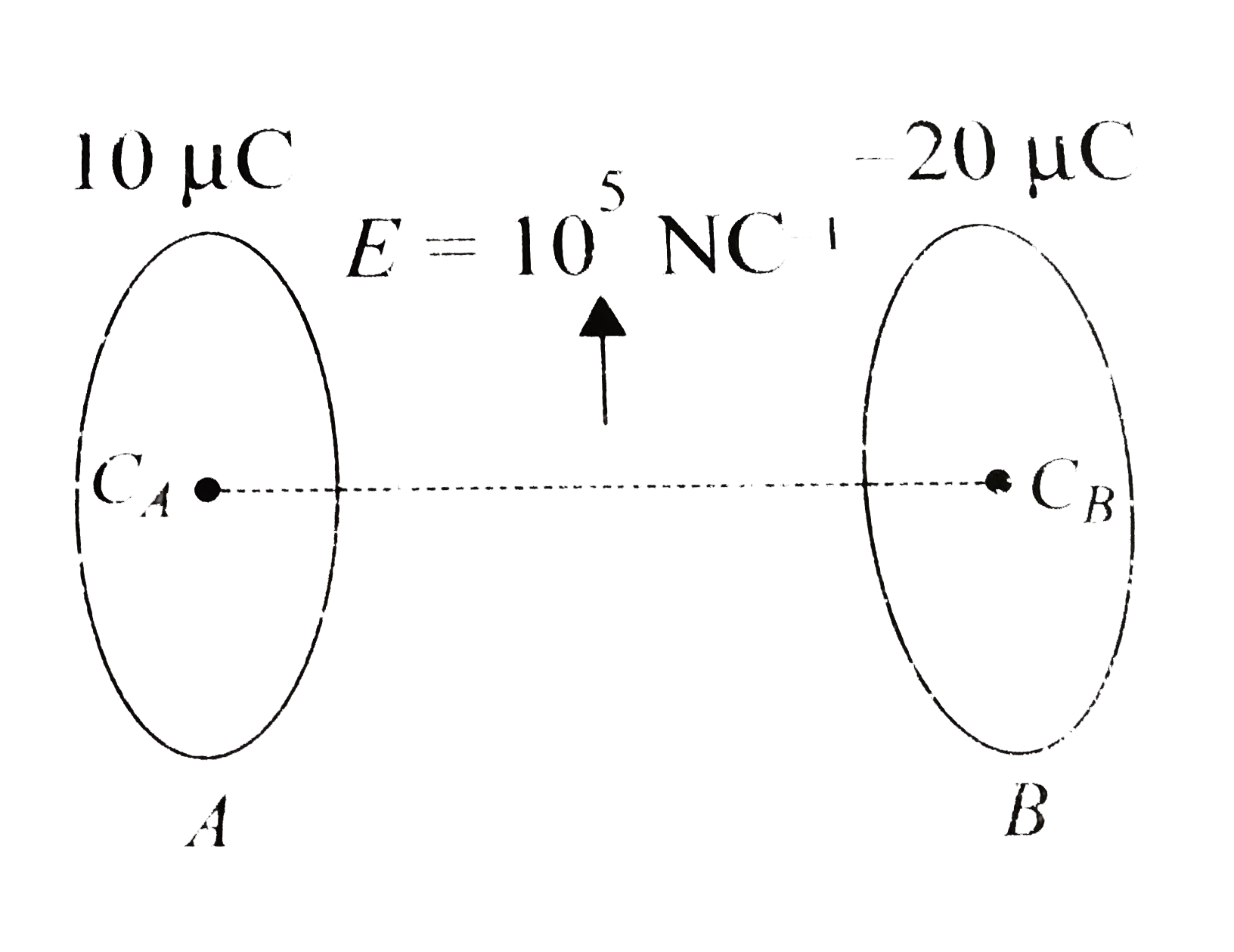
Work done by electric field, when particle moves from CA→CB is
−1.2J
1.2 J
−3.6J
3.6J
The correct Answer is:D
W=q(V2−V1)=9×10−2[(100.3−2005)−(100.5−200.3)]
=3.6J
Since only conservative forces act on the system, potential energy changes to kinetic energy.
3.6=12mv2 or v2=72 or v=6√2ms−1
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Interger Answer type
20 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Fill in the blanks
10 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Assertion and Reason Type
8 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - CENGAGE PHYSICSCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Question Bank
4 Videos
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer
12 Videos
Similar Questions
Two circular rings A and B each of radius a = 30 cm are placed coaxially with their axis horizontal in a uniform electric field E=105NC−1 directed vertically upward as shown in figure. Distance between centers of the rings A and B (CAandCB)is40cm. Ring A has positive charge qA=10μC and B has a negative charge qB=−20μC. A particle of mass m and charge q=10μC is released from rest at the center of ring A. If particle moves along CACB, then
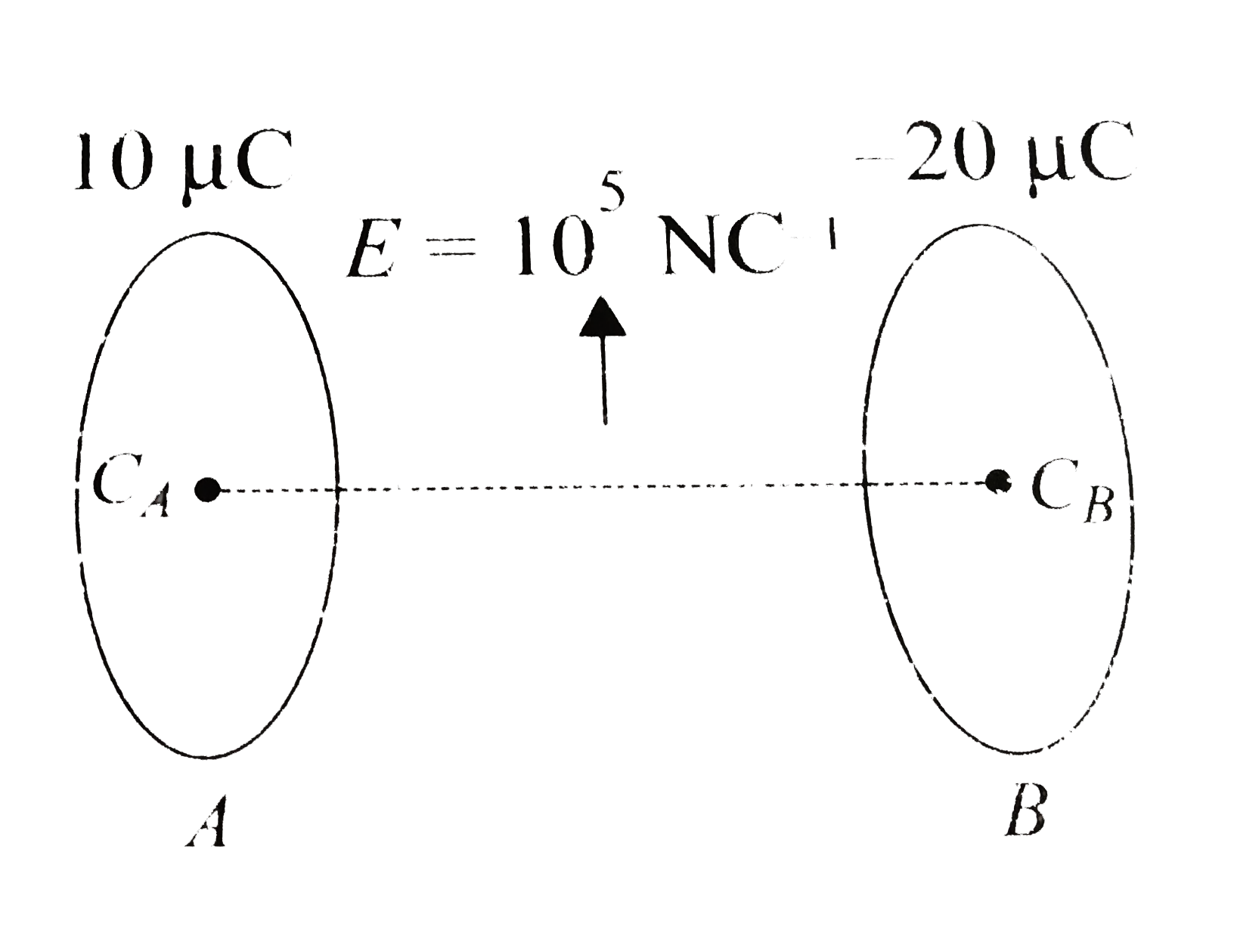
Speed of particle when it reaches at center of B is
View SolutionTwo circular rings A and B each of radius a=30cm are placed co-axially with their axes horizontal in a uniform electric field E=105N/C directed vertically upward as shown in the figure. The distance between the centers of these rings A and B is h=40cm. Ring A has a positive charge q1=10μC while ring B has a negative charge of magnitude q2=20μC. A particle of mass m = 100 gm and carrying a positive charge q=10μC is released from rest at the centre of the ring A. Calculate its velocity when it has moved a distance 40 cm.
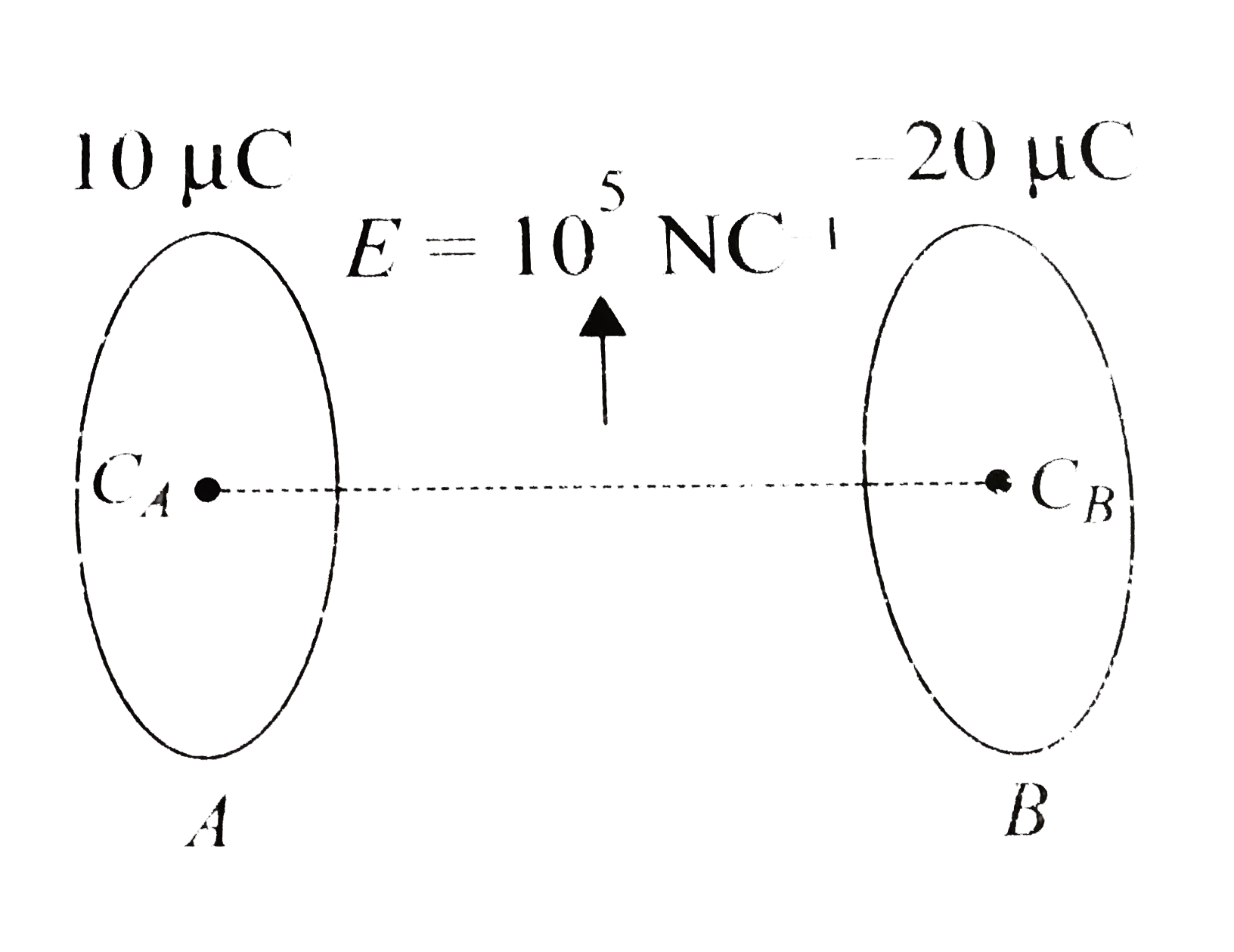
View Solution
Knowledge Check
Two circular rings A and B each of radius a = 30 cm are placed coaxially with their axis horizontal in a uniform electric field E=105NC−1 directed vertically upward as shown in figure. Distance between centers of the rings A and B (CAandCB)is40cm. Ring A has positive charge qA=10μC and B has a negative charge qB=−20μC. A particle of mass m and charge q=10μC is released from rest at the center of ring A. If particle moves along CACB, then
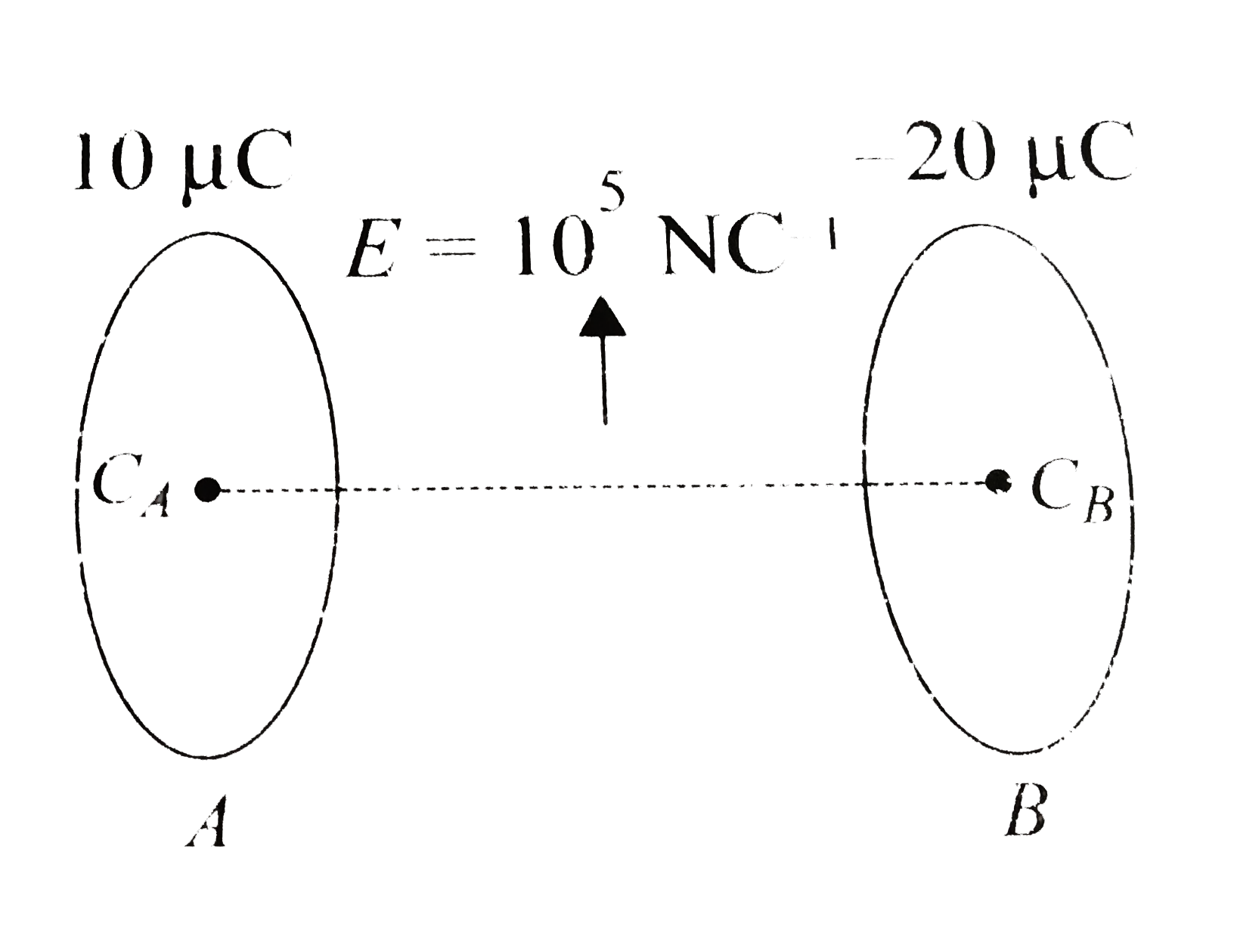
Speed of particle when it reaches at center of B isA6√2m/sB12√2m/sC2√6m/sD4√6m/sA thin conducting ring of radius R is given a charge +Q, Fig. The electric field at the center O of the ring due to the charge on the part AKB of the ring is E. The electric field at the center due to the charge on part ACDB of the ring is
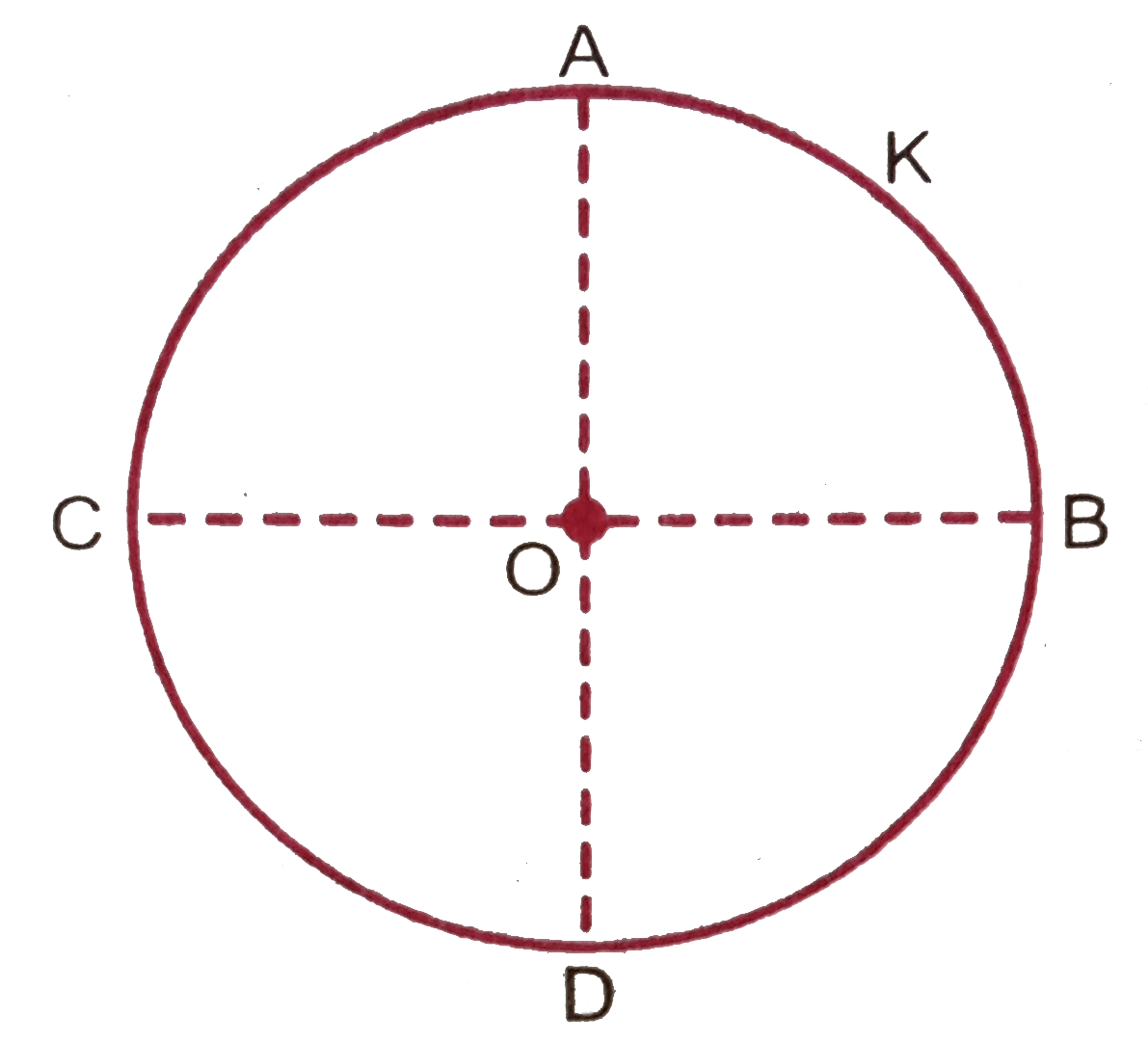 A3E along KOBE along OKCE along KOD3E along OK
A3E along KOBE along OKCE along KOD3E along OK
Two identical circular rings A and B of radius 30 cm are placed coaxially with their axes horizontal in a uniform electric field E.=105N/C directed vertically upward as shown in figure. Distance between centres ofthese rings A and B is40cm. Ring A has a positive charge 10μC while ring B has a negative charge of magnitude 20μC. A particle of mass 100g and carrying a positive charge 10μC is released from rest at the centre of the ring A. Calculate its velocity when it has moved a distanceof40cm. Take g=10m/s2
[6√2m/s]
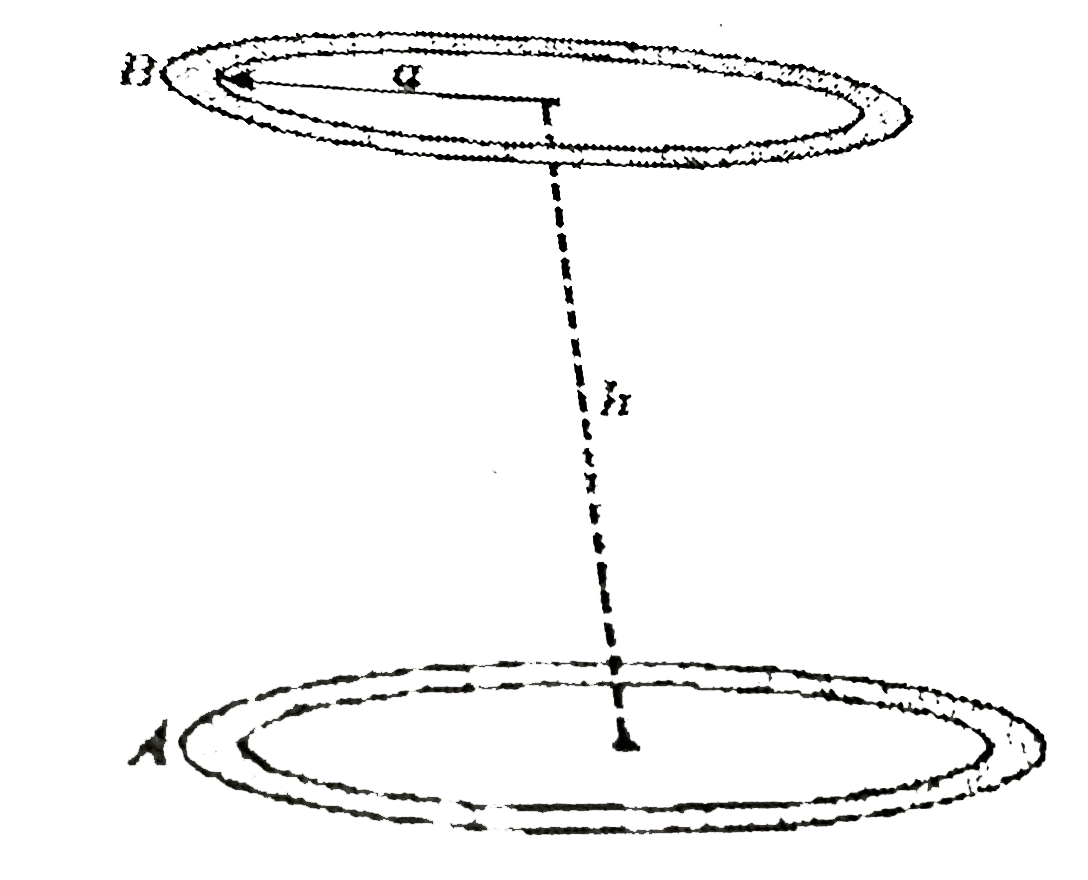
View SolutionTwo circular rings A and B, each of radius a = 30cm, are placed coaxiallywith their axes vertical as shown in figure−1.456. Distance between centres of these rings is h=40cm. Lower ring A has a positive charge of 10μC, while upper ringB has a negative charge of 20μC. A particle of mass m=100 gm carrying a positive charge of q=10μ C is released from rest at the centre of the ring ltbergt (a) Calculate initial acceleration of the particle.
(b) Calculate velocity of particle when it reaches at the centre ofupper ring B. (g=10ms−2)
View SolutionA charge of 500 μC is distributed uniformly over the circumference of a ring of radius 25 cm. What will be be electric potential at the centre of ring?
View SolutionTwo co-axisal rings, each of radius R, are separated by a small distance l(ltltR) and carry charges q and -q.Find the electric potential and field at a point on the axis at a distance x from the midpoint between the rings,
View SolutionPositive and negative charges of 1μC each are placed at two points as shown in the figure. Find the potential difference between A and B
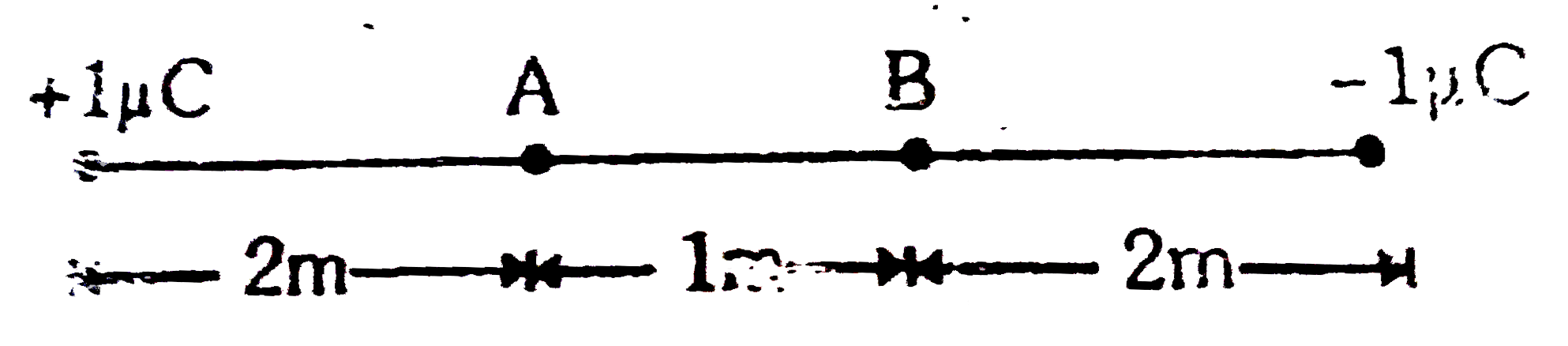
View SolutionPositive and negative charges of 1μC each are placed at two points as shown in the figure. Find the potential difference between A and B
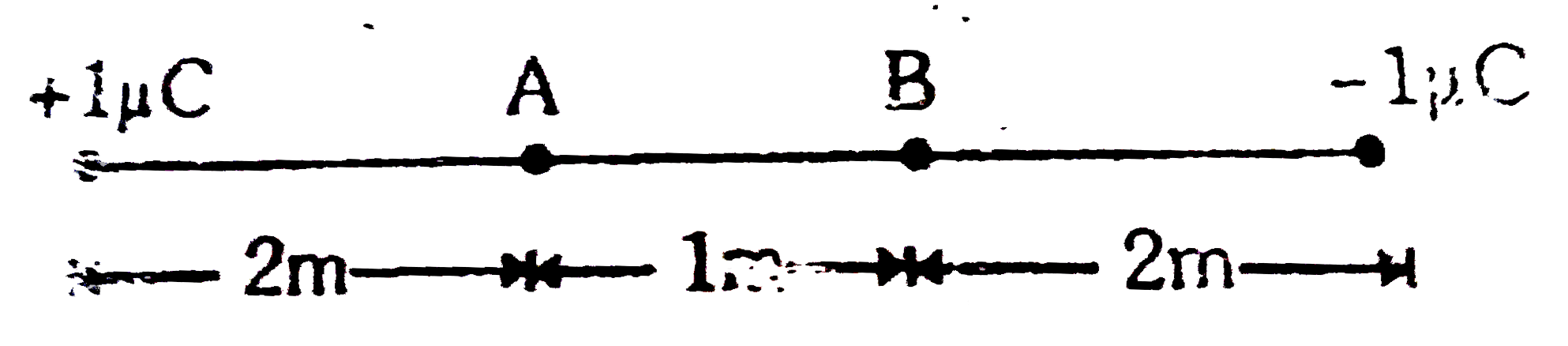
View Solution
