If net flux through a Caussian surface is zero, then find whether the following statements are correct or not.
The number of field lines entering the surface equals to the number of field lines leaving the surface.
To determine whether the statement "The number of field lines entering the surface equals the number of field lines leaving the surface" is correct when the net flux through a Gaussian surface is zero, we can follow these steps:
1. Understanding Electric Flux:
- Electric flux (Φ) through a surface is defined as the product of the electric field (E) and the area (A) through which it passes, taking into account the angle (θ) between the field lines and the normal to the surface. Mathematically, it is given by:
Φ=∫→E⋅d→A
2. Applying Gauss's Law:
- According to Gauss's Law, the net electric flux through a closed surface (Gaussian surface) is proportional to the charge (Q) enclosed within that surface:
Φ=Qencε0
- If the net flux is zero, it implies that the enclosed charge Qenc=0.
3. Interpreting Zero Net Flux:
- A net flux of zero means that the total number of electric field lines entering the surface is equal to the total number of electric field lines leaving the surface. This is because the lines entering the surface contribute negatively to the flux, while the lines leaving contribute positively.
4. Conclusion:
- Therefore, if the net flux through the Gaussian surface is zero, it follows that:
Number of field lines entering the surface=Number of field lines leaving the surface
- Thus, the statement is correct.
Final Answer:
The statement "The number of field lines entering the surface equals the number of field lines leaving the surface" is correct when the net flux through a Gaussian surface is zero.
- Electric flux (Φ) through a surface is defined as the product of the electric field (E) and the area (A) through which it passes, taking into account the angle (θ) between the field lines and the normal to the surface. Mathematically, it is given by:
Φ=∫→E⋅d→A
- According to Gauss's Law, the net electric flux through a closed surface (Gaussian surface) is proportional to the charge (Q) enclosed within that surface:
Φ=Qencε0
- If the net flux is zero, it implies that the enclosed charge Qenc=0.
- A net flux of zero means that the total number of electric field lines entering the surface is equal to the total number of electric field lines leaving the surface. This is because the lines entering the surface contribute negatively to the flux, while the lines leaving contribute positively.
- Therefore, if the net flux through the Gaussian surface is zero, it follows that:
Number of field lines entering the surface=Number of field lines leaving the surface
- Thus, the statement is correct.
The statement "The number of field lines entering the surface equals the number of field lines leaving the surface" is correct when the net flux through a Gaussian surface is zero.
Similar Questions
If net flux through a Caussian surface is zero, then find whether the following statements are correct or not.
There are no changes inside the surface.View SolutionIf net flux through a Gaussian surface is zero, then find whether the following statements are correct or not.
The net charge inside the surface is zero.View SolutionIf net flux through a Caussian surface is zero, then find whether the following statements are correct or not.
The electric field just outside a charged conductor is perpendicular to the surface of the conductor and has a magnitude of σ/2ε0 where σ is the charge per unit area at that point.View SolutionFind out flux through the given Gaussian surface.
 View Solution
View SolutionFind flux through the hemispherical surface
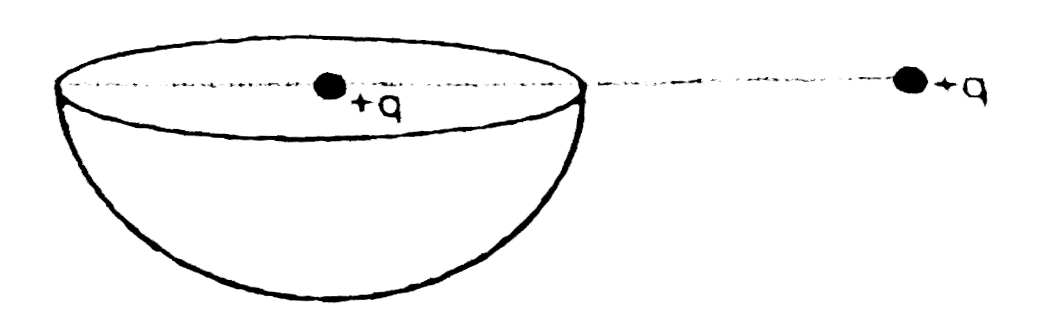 View Solution
View SolutionAn imaginary closed surface P is constructed around a neutral conducting wire connected to a battery and a switch as shown in figure. As the switch is closed, the free electrons in the wire start moving along the wire. In any time interval, the number of electrons entering the closed surface P is equal to the number of electrons leaving it. On closing the switch, the flux of the electric field through the closed surface :
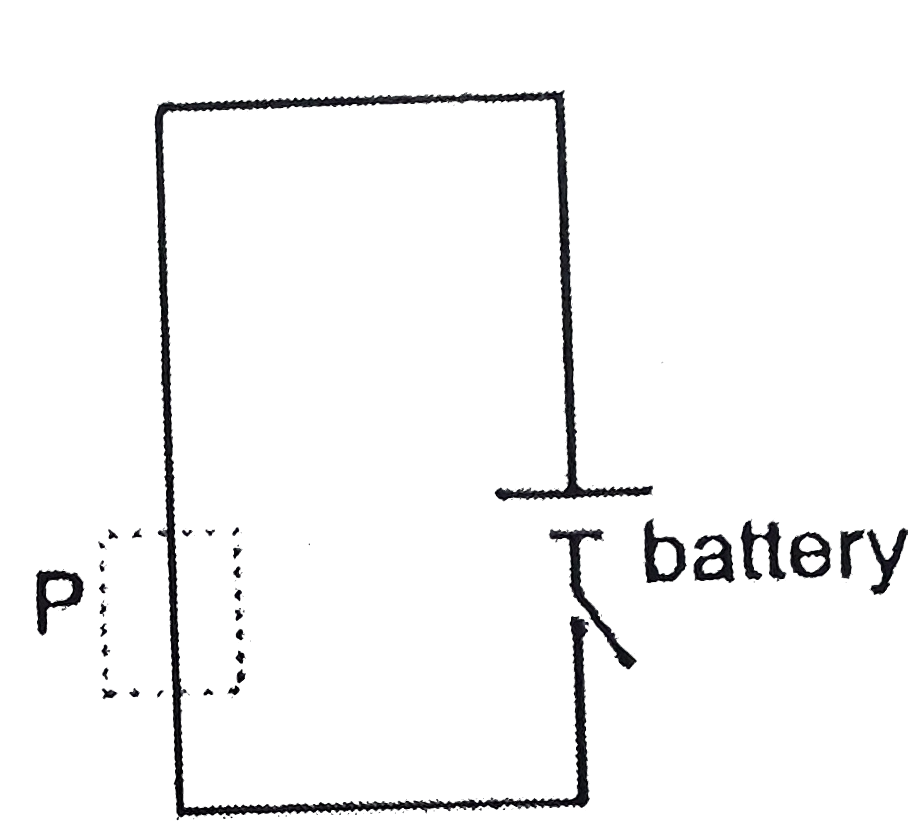 View Solution
View SolutionA closed surface S is constructed around a conducting wire connected to a battery and a switch (figure 30-Q6). As the switch is closed, the free electrons in the wire start moving along the wire. In any time interval, the number of electrons entering the closed surface S is equal to the number of electrons leaving it. On closing the switch, the flux of the electric field through the closed surface
 View Solution
View SolutionIf the flux of the electric field through a closed surface is zero,
View SolutionThe net flux passing through a closed surface enclosing unit charge is
View SolutionIdentify the correct statement bout the magnetic field lines.
View Solution
