A 1.0 cm thick plate of dielectric material is placed midway between two copper plates 3.0 cm apart. If the capacity before introducing the dielectric is C1 and after introducing dielectric C2. (K is dielectric constant).
C1/C2=32+1/k
C1/C2=13(2+k)
C1/C2=13(2k+1)
C1/C2=13(1k+2)
The correct Answer is:D
To solve the problem, we need to find the ratio of the capacitance before and after introducing the dielectric material between the plates. Let's denote the following:
- D = distance between the plates = 3.0 cm = 0.03 m
- T = thickness of the dielectric = 1.0 cm = 0.01 m
- K = dielectric constant of the material
- C1 = capacitance before introducing the dielectric
- C2 = capacitance after introducing the dielectric
Step 1: Calculate C1
The capacitance C1 of the parallel plate capacitor without the dielectric is given by the formula:
C1=ϵ0AD
where:
- ϵ0 is the permittivity of free space,
- A is the area of the plates,
- D is the distance between the plates.
Step 2: Calculate C2
When the dielectric is introduced, the effective distance between the plates becomes D−T. The capacitance C2 with the dielectric is given by:
C2=ϵ0AD−T⋅K
Step 3: Find the ratio C1C2
Now, we can find the ratio of the capacitances:
C1C2=ϵ0ADϵ0AD−T⋅K
This simplifies to:
C1C2=D−TD⋅1K
Step 4: Substitute the values
Substituting D=0.03 m and T=0.01 m into the equation:
C1C2=0.03−0.010.03⋅1K
This simplifies to:
C1C2=0.020.03⋅1K=23⋅1K
Step 5: Final expression
Thus, the final expression for the ratio of capacitances is:
C1C2=23K
- T = thickness of the dielectric = 1.0 cm = 0.01 m
- K = dielectric constant of the material
- C1 = capacitance before introducing the dielectric
- C2 = capacitance after introducing the dielectric
- ϵ0 is the permittivity of free space,
- A is the area of the plates,
- D is the distance between the plates.
Similar Questions
The distance between the plates of a parallel plate capacitor is 0.04m A field of 5000V/m is established between the plates and an unchanged metal plate of thickness 0.01m is inserted intothe condenser parallel to its plate. Find the p.d. between the plates (a) before the introducing of the metal plate and (b) after its introduction. what would be the p.d. if plate of dielectric constant K=2 is introduced in place of metal plate?
View SolutionA dielectric slab of thickness 1.0 cm and dielectric constant 5 is placed between the plates of a parallel plate capacitor of plate area 0.01m2 and separation 2.0 cm. Calculate the change in capacity on introduction of dielectric. What would be on the change, if the dielectric slab were conducting?
View Solution
Knowledge Check
Assertion: The distance between the parallel plates of a capacitor is halved, then its capacitance is doubled.
Reason: The capacitance depends on the introduced dielectric.AIf both assertion and reason are ture and reason is the correct explanation of assertion.BIf both assertin and reason are ture but reason is not the correct explanation of assertion .CIf assertion is true but reason is false.DIf both assertion and reason are false.
A parallel plate capacitor with air between the plates has capacitance of 9pF. The separation between its plates is 'd'. The space between the plates is now filled with two dielectrics. One of the dielectrics has dielectric constant k1=3 and thickness d3 while the other one has dielectric constant k2=6 and thickness 2d3. Capacitance of the capacitor is now
View SolutionA parallel plate capacitor with air between the plates has capacitance of 9pF. The separation between its plates is 'd'. The space between the plates is now filled with two dielectrics. One of the dielectrics has dielectric constant k1=3 and thickness d3 while the other one has dielectric constant k2=6 and thickness 2d3. Capacitance of the capacitor is now
View SolutionA parallel plate capacitar, of capacitance, 20μF, is connected to a 100 V supply. After some time, the battery is disconnected , and the space, between the plates of the capacitor is filled with a dielectric, of dielectric constant 5. Calculate the energy stored in the capacitar (i) before (ii)after dielectric has been put in between its plates.
View SolutionHalf of the space between the plates of a parallel plate capacitor is filled with dielectric material of constant K. Then which of the plots are possible?
View SolutionA parallel plate capacitor without any dielectric has capacitance C0. A dielectric slab is made up of two dielectric slabs of dielectric constants K and 2K and is of same dimensions as that of capacitor plates and both the parts are of equal dimensions arranged serially as shown. If this dielectric slab is introduced (dielectric K enters first) in between the plates at constant speed, then variation of capacitance with time will be best represented by :

View SolutionSeparation between the plates of parallel plate capacitor is 5 mm. this capacitor, having air as the dielectric medium between the plates, is charged to a potential difference 25 V using a battery. The battery is then disconnected and a dielectric slab of thickness 3mm and dielectric constant K=10 is placed between the plates as shown. potential difference between the plates after the dielectric slab has been introduced is-
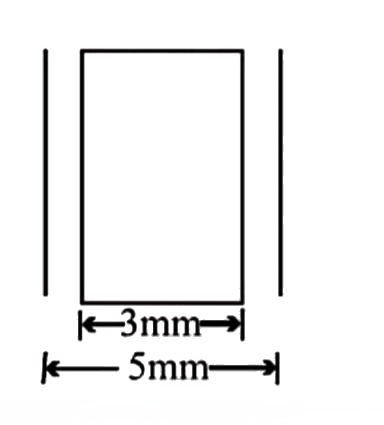
View SolutionThe parallel combination of two air filled parallel plate capacitor of capacitance C and nC is connected to a battery of voltage, V. When the capacitors are fulley charged, the battery is removed and after that a dielectric material of dielectric constant K is placed between the two plates of the first capacitors. the new potential difference of the combined system is
View Solution
